B+ (Plus) Tree in DBMS

What is a B+ tree?

The B+ tree is known as a balanced binary search tree. in this tree, we can store the data in the form of nodes. B+ tree always has the following multi-level index format so we can store data easily.

B+ tree stores all the data in the leaf node and all the indices are stored in the internal nodes. In the B+ tree, every leaf node is on the same height and all the nodes are linked to other nodes. B+ tree always starts with a head node or root node and the root node must contain a minimum of two child nodes.

The concept of a balanced binary search tree or a B+ tree is very important because it is more convenient in terms of operation as well as efficient. In a B+ tree, we always denote the actual pointers so that we can access data easily without any problem. We can also link the leaf node with the help of a link list.

Properties of B+ Tree

There are some properties of the B+ tree as follows:

• In the B+ tree, we store all the data in the form of nodes or in the leaf node.
• All the indices are stored in the form of internal nodes.
• All the nodes are present at the same height of the tree.
• In the B+ tree, all the nodes are linked with other nodes.
• B+ tree contains a head node/root node that should have a minimum of 2 child nodes.
• In the B+ tree, each node has a maximum of m child node except the root node and a minimum of m/2 children.
• In the B+ tree, each node can contain minimum[m-2]-1 keys and maximum m-1 keys.

Structure of B+ Tree in DBMS

B+ tree contains all the nodes or leaf nodes at equal distances from the root node.

The B+ tree is of the order n where n is fixed for every node in the B+ tree.

B+ tree contains two types of nodes:

• Internal node
• Leaf node

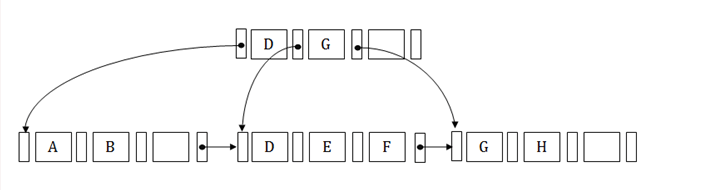
Internal Node

An internal node is also known as an inner node. It is a type that has one child node.

In other words, the internal node is a node that has child nodes in the B+ tree. The internal node contains at least the n/2 record pointer in the B+ tree except the root node. An internal node contains at most n pointer in the B+ tree.

Leaf node

A leaf node is also known as an external node. It is a type of node that has no child node in the B+ tree. In other words, the leaf node can contain at least n/2 records pointer and n/2 key values in the B+ tree.

In the B+ tree, a leaf node contains at most n record pointers         and n key values. In the B+ tree, every leaf node must contain block pointer A to a point to the next leaf node.

Difference between B and B+ trees in DBMS

S.no.	B Tree	B+ Tree
1	We can store data in internal nodes as well as an external nodes.	In the B+ tree, we only can store data in the leaf node.
2.	In the B tree, Operations like insertion, deletion, and searching are slower to execute.	In the B+ tree, Operations like insertion, deletion, and searching are faster to execute.
3.	In the B tree, there is no redundant search key are present.	In the B+ tree, there is redundant search keys are present.
4.	In the B tree, leaf nodes are not linked to each other.	In the B+ tree, leaf nodes are linked with the other leaf node.
5.	They are not advantageous as compared to B+ trees, and hence, they are not used in the database management system.	They are advantageous as compared to B trees, and hence, because of their efficiency, they find their applications in the database management system.

Operations in B+ tree in DBMS

In the B+ tree, we can perform so many operations of insertion, deletion, and searching a node in a B+ tree.

• Insertion
• Deletion
• Searching

Insertion in B+ Tree

Insertion is a process in which we can insert any data in the B+ tree in the form of nodes.

We can insert value in the leaf node of the B+ tree. There are 2 cases of insertion as follows:

• Case 1: In the first case of insertion, if the leaf node is empty then we can simply insert the value into the leaf node in the B+ tree in increasing order if the leaf node is not full.
• Case 2: In the second case of insertion, if the leaf node is full then we need to follow some procedure or steps as follows:

Step 1: first we need to insert the new node in the leaf node in increasing order but the leaf node is already full, we need some balancing in the node to store the value.

Step 2: now we need to break the node in the B+ tree at the m/2 position.

Step 3: After breaking the node, we add the m/2 value to the parent node of the B+ tree.

Step 4: if the parent node is full then in this case we just repeat steps 2 and 3.

Let's understand by an example:

Example:

First, we need to create the B+ tree with the help of this data: 1,4,7,10,17,21,31

Let's suppose our B+ tree is in the order(m) that is 4. Now max children= 4, and minimum children: m/2 =2 and to find the max keys(m-1):4-1=3 and to find the min keys(m/2)-1: (4/2)-1= 1

Now, first we will insert the values 1,4 and 7 into the first node of the B+ tree.

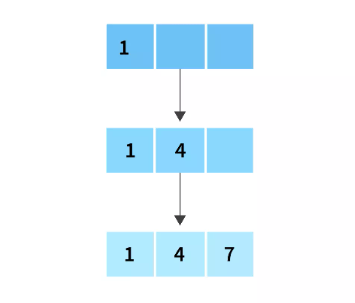
After the insertion of 1,4 and 7, now we will insert the next element 10, but you can see there is no space in the current node(because we can only store a maximum of 3 keys in a node), we need to split the node.

Now, we need to spilt between 4 or 7 nodes. If we choose 4 then the tree will be left biased tree. And if we choose 7 then the tree will be the right-biased tree. We can choose one of them.

Let’s choose a right-based tree for this example. Now, we split node 7 and after that, we move it up.

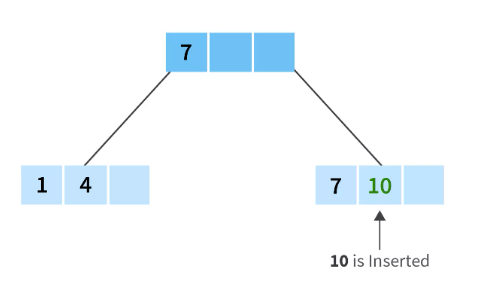
After inserting 10, now we will split it into:

1. 1,4 and a blank space ( because the maximum number of keys in a node can be 3) and,
2. We will insert the next value 17 into the 7 and 10 nodes and it will come after 10 in the ascending order.

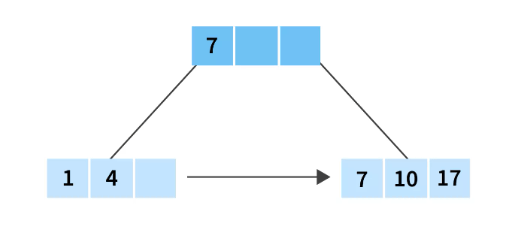
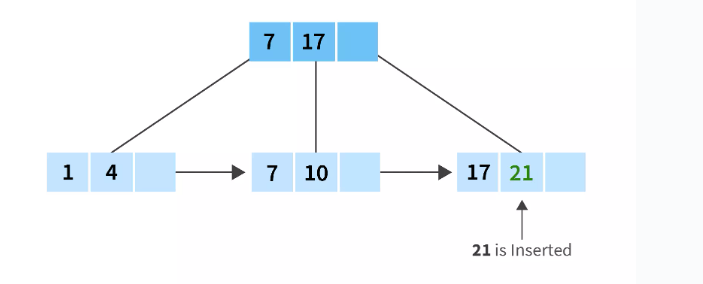
Now, we will insert 21 and preferably, it should be placed after 17. But the node is full because of 3 keys. We need to split the node, as we all know that we choose the right biased tree after step 2, so we will split the node in the same way.

1. 7,10 and a blank space
2. And 17,21 and a blank space

And finally, we will insert last element in the node that is 31, it should be placed after 21 in the last leaf node of the B+ tree. And after the insertion of 31, our tree is complete.

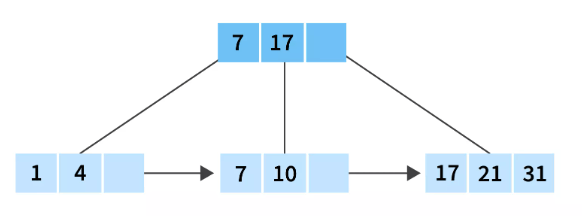
And all the nodes have a minimum of 2 children, which satisfies the fact that we deduced the B+ tree before the insertion in the B+ tree.

Deletion in B+ tree

Deletion is a process when we delete the data or value/keys from the tree. In other words, if we want to delete some value from the node in the B+ tree, we use the deletion operation to perform that task.

Similar to insertion, deletion also follows two cases for deleting any value from the B+ tree.

Case 1: Let's suppose we want to delete the value that is present only in the leaf node of the B+ tree.

If the value to be deleted is present in the leaf node only then we simply delete the value easily.

Case 2: Let's suppose the value to be deleted is present in the leaf node and also has a pointer to it as well then first, we need to locate the node that we want to delete and remove it from the leaf node, but we also need to remove it from the index of the B+ tree that points to this node.

Let’s take an example to understand the deletion in the B+ tree.

Example:

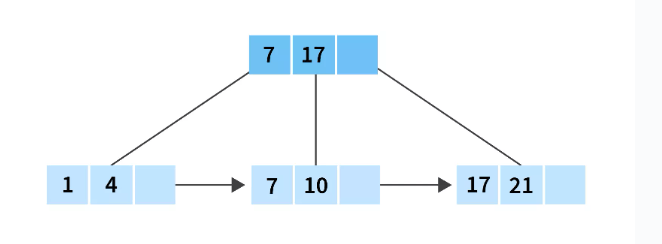
Suppose we want to delete 21 from the form of the leaf node in the B+ tree.

We will simply delete the value from the B+ tree.

Before deletion:

After the deletion:

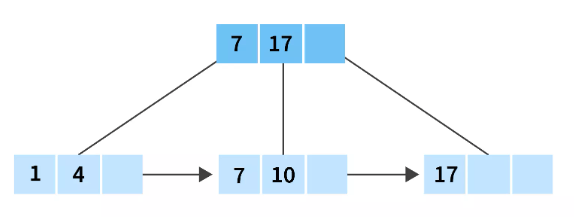
So 21 is present in the leaf node of the B+ tree and if we delete the value it will not invalidate the minimum number of keys which is 1, so we can simply delete the value from the leaf node.

Searching in the B+ Tree

Searching is an operation in which we can search for the element we want from the leaf node that is present in the B+ tree.

In the B+ tree, searching is very simple because the leaf node is linked with another leaf node with the help of pointers.

Searching can be done in a B+ tree following some specific steps or we can say with the help of an algorithm.

1. First, we will perform a binary search in the B+ tree to find the current node records.
2. After performing a binary search, if we get the matching record that we want then we will simply return it.
3. And,, if we didn’t find the desired data then the current node is a leaf node and the key is not present in the B+ tree.
4. Else, we just repeat all the steps from the beginning.

Let's understand searching by an example:

Example 1:

Suppose we want to search the element 10 from the B+ tree.

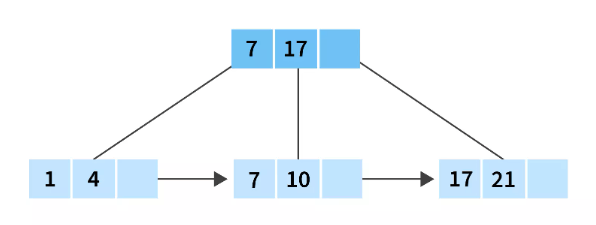
First, we compare element 10 with the starting node which is 7 and 17. as we all know 10 lies between them, so we simply need to search in the records between 7 and 17. Since 7 and 17 are leaf nodes we will get the desired value which is 10  in this case.

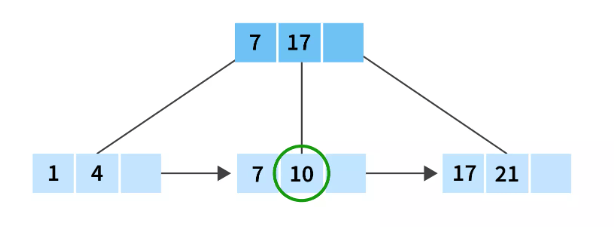
Let's take one more example:

Example 2:

Suppose we want to search element 45 on the following B+ tree.

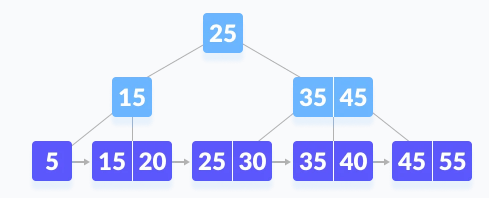
Let’s take k= 45, now we compare k with the root node of the B+ tree.

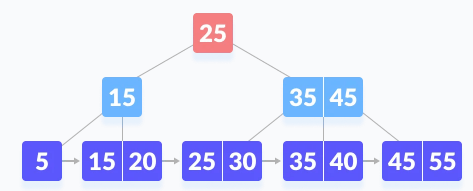
K is not found in the root node, now we know k>25 so, we will go to the right child node.

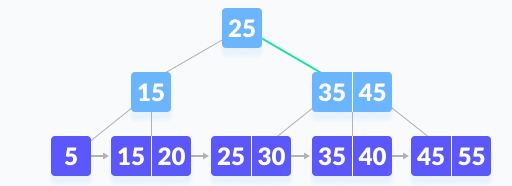
Now we will compare k with 35. Now that k is also greater than 35, we will compare k with 45.

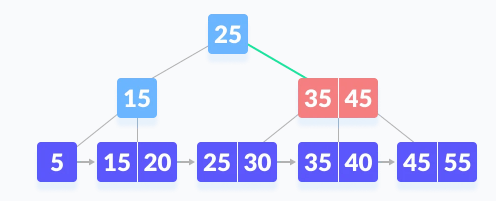
Since there is two 45 present in the B+ tree and k=>45, so we simply go to the right child node.

We will get the value of k which we want, so it will return the value of k and searching will stop now.

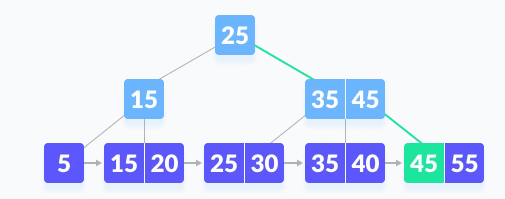
That is the searching operation in the B+ tree.

Advantages of B+ Tree in DBMS

As we all know that B+ trees are better than B trees. Now let's discuss the advantages of the B+ tree in some points:

• In the B+ tree, height of the tree is always balanced and comparability is less than in the B tree.
• B+ tree always takes an equal number of disk access to fetch data.
• In the B+ tree, we use keys for the indexing of the nodes.
• In the B+ tree, we store the data in the form of leaf nodes, so searching is very easy as well as faster compared to the B tree.
• In the B+ tree, we can access the stored data easily sequentially as well as directly.

Disadvantage of the B+ Tree in DBMS

There is some minor disadvantage of the B+ tree:

• Extra insertion
• Deletion overhead
• Space overhead etc.

Application of B+ Tree in DBMS

B+ tree contains some applications. The application of the B+ tree is as follows:

• B+ tree is very useful in DBMS because it supports equality and range search.
• In the B+ tree, we also can facilitate database indexing in database management systems.
• With the help of the B+ tree, we can access the actual data that are present in the disk faster.
• It also supports multi-level indexing for operating fast compared to the B+ tree.