Derivation Tree of Context Free Grammar - Automata
Derivation Tree of Context Free Grammar
Derivation tree gives a way to show how a string can be derived from context free grammar. It is also called as parse tree, production tree, and syntax tree. The interior nodes of derivation tree are labeled with variables and leaves of this tree are labeled with terminals. We can also say that left-hand side of production rules is always interior nodes, and the right-hand side of production rules may be exterior nodes. The root of the derivation tree is labeled with start symbol or variable.
Formal Definitions of Derivation Tree
We can define a derivation tree of context free grammar G = (V, T, P, S). A derivation tree satisfies the following properties:
- The root node of derivation tree is labeled with S.
- Every vertex of derivation tree is labeled with a variable or terminal or an empty symbol.
- Every leaf has a label from T U {?}.
- The label of the interior node is variable V.
- If any node n has label B, and vertices n1, n2 ……………….,nk are the sum of vertex n with labels X1,X2 ……………..Xk respectively then B -> X1X2…………..Xk is production in P.
- If the leaf is labeled with ?, then it must be the only child of its parent.
Types of Derivation Tree
- Left Most Derivation Tree
- Right Most Derivation Tree
- Mixed Derivation Tree
Left Most Derivation Tree:
In left most derivation tree, for each step, production rule is applied to the leftmost variable that’s why it is called left most derivation tree.
Example:
Consider the Context Free Grammar:
S -> S * S
S -> S + S
S -> 0
S -> 1
S -> 2
Find string 0 + 1 * 2
Solution:
Let us derive string 0 + 1 * 2 using left most derivation.
S => S * S
=> 0 + S
=> 0 + S * S
=> 0 + 1 * S
=> 0 + 1 * 2
In this, each step of derivation, the production rule is applied to leftmost variable.
Right Most Derivation Tree:
In right most derivation tree each step, production rule is applied to the rightmost variable that’s why it is called right most derivation tree
Example:
Consider the Context Free Grammar:
S -> S * S
S -> S + S
S -> 0
S -> 1
S -> 2
Find string 0 + 1 * 2
Solution:
Let us derive string 0 + 1 * 2 using left most derivation.
S => S + S
=> S + S * S
=> S + S * 2
=> S + 1 * 2
=> 0 + 1 * 2
In this, for each step of derivation the production rule is applied to rightmost variable
Mixed Derivation Tree:
In a derivation, if the production rule is not applied to left most variable in each step or right most variable in each step, then it is called mixed derivation.
Example:
Consider the Context Free Grammar:
S -> S * S
S -> S + S
S -> 0
S -> 1
S -> 2
Find string 0 + 1 * 2
Solution:
Let us derive string 0 + 1 * 2
S => S + S
=> S + S * S
=> 0 + S * S
=> 0 + S * 2
=> 0 + 1 * 2
In each step of derivation, the production rule is applied to both leftmost and rightmost variable.
Let us take some examples of derivation tree
Example:
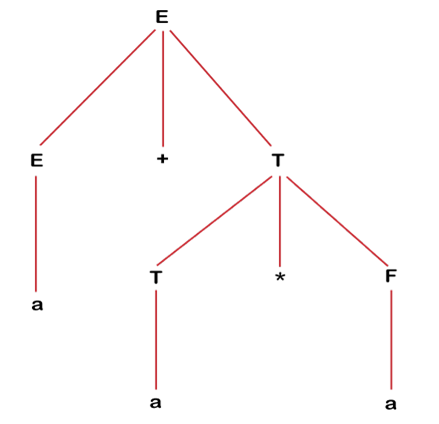
Consider the context free grammar G = (V, T, P, S)
Where,
S -> 0S1
V = {E, T, F}
T = {a, +,*, (,)}
S is the start symbol.
P is the set of production rules in context free grammar, which are defined as follows:
E -> E + T | T | a
T -> T * F | F | a
F -> (E) | a
Find derivation of string a + a * a
Solution:
Let us see derivation of string a + a * a
E => E + T
=> E + T * F
=> a + T * F
=> a + a* F
=> a + a* a
The derivation for string a + a * a is shown below: