Basics Vectors in Linear Algebra in ML
First, to learn Machine Learning sincerely, we must know about vectors in Linear Algebra. The principle of Linear Algebra is very much important here. Linear Algebra is the study of lines, spaces, and planes and the survey of some techniques for linear transformation. A basis is the vector set that generates all the vector spaces from Linear Algebra.
When we look at the basis of the matrix image, we remove all the redundant vectors from the matrix. Therefore basis is just a combination of all the linear independent equation vectors. Every nonzero vector space has a basis.
What is the idea of basis vector?
The idea behind the basis vector is as follows:
Let's take a set K where K contains all the two-dimensional matrices. We have to take all the two-dimensional matrices on that sets. So there will be so many vectors of the 2-dimensional matrix. All the equations of the vector will be valid in these spaces.
So, if there are two vectors, let vector (v1 and v2), and then they form the basis and vector in this space. These two vectors are written in a Linear Algebraic equation. And now, we notice that these Linear Algebraic equations are actually in the form of numbers.
For example: If you want vector (5, 6), then this is written in the form of Linear Algebraic equations (1, 0) and (0, 1) with the scalar multiplication of 5 and 6, respectively. So the main key point is that if we have many numbers of vector space, these are written in the form of two simple Linear Algebraic equations (1, 0), and (0, 1) with the multiplication of scalar quantity, respectively.
Definition of basis vector
If you want to write the linear combination of every vector in a given space, these independent vectors are called the basis vector of a shared space.
Properties
1. It must be linear independent
It is impossible if we want to derive the value of vector v2 by multiplying a scalar quantity. And it is also proved that these two vectors should be linear and independent of each other. And this is the essential information to generate the unique vector.
2. The whole space must be span
Here span means any vector that presents in that space. We can write both vectors on that particular space.
3. These basis vectors are not unique
We can find many sets of the basis vector. But there are only two conditions that we have to know before selecting the basis vectors. These rules are that they should be independent of each other, and they should spam in nature.
Points to remember
Interestingly, we can have two vectors if they have a different set of numbers. Let us discuss it with an example. Let's see if we have two vectors, v1(1,0) and v2(0,1), similarly by taking another example, v1(1,1) and v2(1,-1). First, we must check whether the number containing both vectors is equivalent. So, if the vector space is the same, then the number of vectors in the set should be the same.
Let's take an example of a space which has four components.

Then arrange the vectors in a matrix form.
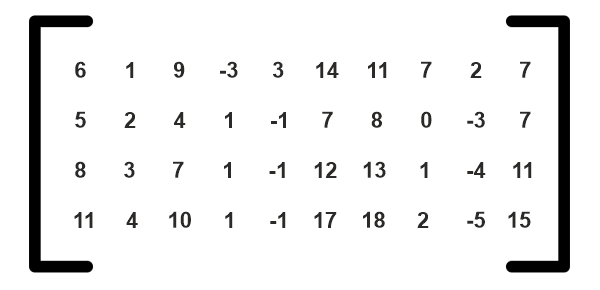
Then we have to identify the rank of the matrix; after that, we know the number of rows and columns in the matrix. Then from the above matrix, we can select two independent columns as basis vectors. It means the number of vector spaces depends on rank. If we have rank 1, then we have just only one vector. We need to represent every matrix in this vector space. So we have to select two vector matrices which are linear and independent of each other, which could be spam.
The view point vector concept from data science is essential for machine learning. For example, if we have ten samples containing four numbers, then we have just 40 numbers.
Let's take another example.
We take two basis vectors, which gives us- 4x2= 8 numbers.
Then from the remaining eight samples, we store two numbers as constant.
Hence, we can store 24 numbers and we can store the whole data in 24 constraints. It is essential to understand the fundamental concept of Data Science. Through this process, we can store the data more innovatively.