Stacking in Machine Learning

Using stacking, you may combine different classification and regression models. The two most well-known group modeling techniques are bagging and boosting. Bagging allows the averaging of several comparable models with significant swings in order to reduce variance. Whereas, Boosting creates several incremental models to reduce the bias while maintaining a low variation.

An alternative concept is termed stacking which is also known as stacked generalization. Exploring a space of several models for the same problem is the goal of stacking. The main concept is that it may approach a learning issue with several sorts of models that can learn a portion of the problem but not the entire problem space. As a result, one can create a variety of learners and utilize them to create final forecasts, one for each learned model. Then you include a new model that picks up on the same goal from the intermediate forecasts.

A machine learning approach which is known as stacking combines the results of many models to get a single, improved forecast. The main plan of this approach is to train many models and that too with different advantages and disadvantages on the same data, and then feed the predictions from these models into a meta-model.

VC Dimension in Machine Learning

There are several stacking variants, and they are:

-Simple Stacking: Before feeding the outputs of the base models to the meta-model, the original features are combined.

- Blending is the process of making a forecast by averaging or weighting the predictions from the base models rather than training a meta-model.

- The final prediction is produced using a process known as recursive stacking, in which the output of the meta-model is given back as input to the underlying models.

Stacking is a potent approach, but to achieve the best results, it demands a lot of data, proper model selection, and hyperparameter optimization.

Stacking for Regression

An ensemble learning approach called stacking combines many models to enhance prediction accuracy overall. In stacking for regression, we train several regression models on the same training data and then utilize it for the predictions from the models as input to a different regression model, termed the meta-regressor, to produce the final prediction.

The basic phases in stacking for regression are as follows:

i)Divide the training data into two parts: the meta-regressor is trained on the first part, and the fundamental regression models are trained on the second portion of the data.

ii) Train multiple base regression models using the training data from the first section. These models might be separate regression model types or the same regression model type but with various hyperparameters.

iii) Make predictions using the trained base regression models for the second set of training data.

iv) When training the meta-regressor on the second portion of the training data, use the predictions from the basic regression models as input features. Any kind of regression model can be the meta-regressor.

v) By first utilising the basic regression models to generate predictions on the test data and then using these predictions as input to the meta-regressor, you can use the trained meta-regressor to make predictions on the test data.

Steps Involved in Making Stack Process

There are various steps that make up the stacking process and some of them are:

1. On the training set of data, training a collection of base models. Any model, including decision trees, support vector machines, and neural networks, may be used in these simulations.

2. Make predictions on a validation set that hasn't been viewed by the trained base models using those models.

3. Use the base model predictions as the input features for the meta-model. Any model, whether a logistic regression or a neural network, may be this meta-model.

4. Train the meta-model using the true values from the verification set and the projections from the basic models.

5. On the test set, use the trained meta-model to generate predictions.

The idea behind stacking is that by combining the projections of several base models, we may obtain a forecast that is more precise and reliable. In order for the greatest accuracy, the predictions are combined using the meta-model.

It is essential to keep in mind that stacking can be relatively costly and necessitates proper hyperparameter optimization. Additionally, it's critical to make sure that the base models are sufficiently varied and do not all commit the same errors because doing otherwise might result in the subpar performance of the stacked model.

Architecture of stack

The following steps are often included in a stack's architecture:

1. The dataset has been divided into two or more subgroups. The basic models are trained using one subset, while the meta-model is trained using the other subset.

2. Training of base models: The initial subset of data is used to train a number of basic models. These models may be of many forms and use various methods. Training a decision tree model, a logistic regression model, and a random forest model are three examples that come to mind.

3. Making predictions using base models: Following training, base models are utilized to make predictions about the output values for the upcoming set of data.

4. Meta model training: A meta-model is developed using the projections from the basic models. This meta-model learns how to mix the results from the base models as input to arrive at a final prediction.

5. Final prediction: The meta-model is then applied to additional data to create the final forecast.

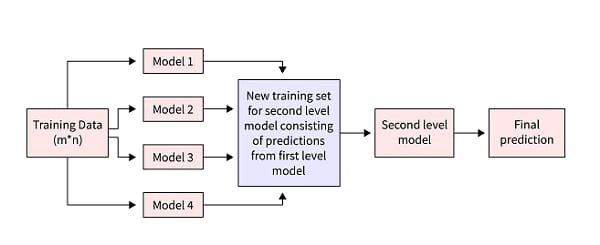
Ways to Implement Stack Model in Machine Learning

There are various ways to implement the stack model and they are:

1. Utilize a stacking classifier: A stacked classifier is also known as a meta-estimator that makes use of the output of several base classifiers as input for a single final classifier. The most accurate estimation is then made by the final classifier.

2. Use a stacking regressor to gather the predictions of many base regressors into a single prediction. This method is similar to that of a stacking classifier. For this function, Scikit-learn offers the StackingRegressor class.

3. Utilise a weighted average: Taking a weighted average of the predictions from the base models is an additional strategy for using a stack model. Using cross-validation or other optimisation methods, the weights may be established.

4. Use a neural network to create a stack model. A neural network may be used to do this. The neural network may be trained to produce the final prediction using the basic models' predictions as input.

5. Construct a stack model using a random forest: A random forest may also be used to construct a stack model. The final prediction may then be made by the random forest using the predictions of the underlying models as its input.

6. Utilize a gradient boosting machine (GBM): A stack model may also be implemented using a GBM. The GBM may be trained to generate the final prediction using the underlying models' predictions as input.

How does Stacking in Machine Learning Work?

The stacking procedure may be divided into the following steps and they are:

1. The training data are divided into K folds.

2. Each of the foundation models needs to be trained on K-1 folds of the data for each fold before being applied to the remaining fold is to create predictions.

3. Gather all of the basic model predictions for each fold, and then train the meta-model on the whole training set using these predictions as input features.

4. On the basis of the test data, use the trained meta-model to generate predictions.

Conclusion

The main concept behind stacking is that, combining a collection of base models in order to generate predictions on the training data. The overall outcomes of these models are then sent into a higher-level model known as a meta-model or processor, which learns how to mix the results of the basic models to produce the outcome. The base models' data or a holdout set of data can be used to train the meta-model.

Any kind of machine learning model, such as linear regression, decision trees, random forests, neural networks, and more, can be used with stacking. It is frequently used in contests where the objective is to get the most accuracy on a test data set. However, stacking may also be utilized in real-world situations to raise forecast accuracy.

Compared to utilizing a single regression model, stacking for regression can increase the predictions' accuracy and adaptability.