Machine Learning Tutorial

What is Machine Learning? Machine Learning Life Cycle Python Anaconda setup Difference between ML/ AI/ Deep Learning Understanding different types of Machine Learning Data Pre-processing Supervised Machine Learning

ML Regression Algorithm

Linear Regression

ML Classification Algorithm

Introduction to ML Classification Algorithm Logistic Regression Support Vector Machine Decision Tree Naïve Bayes Random Forest

ML Clustering Algorithm

Introduction to ML Clustering Algorithm K-means Clustering Hierarchical Clustering

ML Association Rule learning Algorithm

Introduction to association Rule Learning Algorithm

Miscellaneous

Top 5 programming languages and their libraries for Machine Learning Basics Vectors in Linear Algebra in ML Decision Tree Algorithm in Machine Learning Bias and Variances in Machine Learning Machine Learning Projects for the Final Year Students Top Machine Learning Jobs Machine Learning Engineer Salary in Different Organisation Best Python Libraries for Machine Learning Regularization in Machine Learning Some Innovative Project Ideas in Machine Learning What is Cross Compiler Decoding in Communication Process IPv4 vs IPv6 Supernetting in Network Layer TCP Ports TCP vs UDP TCP Working of ARP Hands-on Machine Learning with Scikit-Learn, TensorFlow, and Keras Kaggle Machine Learning Project Machine Learning Gesture Recognition Machine Learning IDE Pattern Recognition and Machine Learning a MATLAB Companion Chi-Square Test in Machine Learning Heart Disease Prediction Using Machine Learning Machine Learning and Neural Networks Machine Learning for Audio Classification Standardization in Machine Learning Student Performance Prediction Using Machine Learning Data Visualization in Machine Learning How to avoid over fitting In Machine Learning Machine Learning in Education Machine Learning in Robotics Network intrusion Detection System using Machine Learning

VC Dimension in Machine Learning
2023-06-15 23:04:48

VC Dimension in Machine Learning

VC stands for Vapnik-Chervonenkis Dimension. Vapnik-Chervonenkis (VC) dimension is a metric used in machine learning to assess the capacity or complexity of a classification method or prediction class. It bears the names of the theory's creators, Vladimir Vapnik and Alexey Chervonenkis.

The size of the biggest group of points indicates that a class may break or perfectly separate, from any marking of those points, known as the VC dimension. It is the most important point that can be organized in any configuration (labeled as positive or negative) while still allowing the hypothesis class to realize that labeling, to put it another way. The VC dimension is k if the class can shatter a set of size k but not any sets of size k+1.

It seems to make sense that a hypothesis class with a higher VC dimension would be more expressive and able to describe functions of greater complexity. The class may be able to fit noise or imaginary patterns in the data, but a greater VC dimension also raises the danger of overfitting.

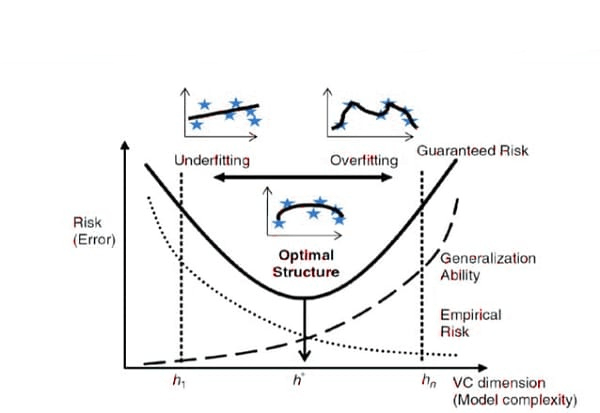
VC Dimension in Machine Learning

The VC dimension has significant effects on learning theory, especially in terms of grasping the sample complexity of learning algorithms. An upper constraint on the number of training instances necessary to guarantee a specific degree of generalization error is provided by the VC dimension.

Usage or Application of VC Dimension

Some of the uses of VC dimensions in machine learning are as follows:

1) VC dimensions may be used to choose the best model complexity for a particular learning challenge. One may choose the capacity of the model required to prevent underfitting or overfitting by taking into account the VC dimension of various hypothesis classes.

2) Generalization bounds: The generalization error of learning algorithms is conceptually restricted by VC dimensions. Based on a model's VC dimension and the size of the training set, these limitations offer assurances for the predicted performance of a model on data that is not observed.

3) Analysis of complexity: The capacity for expression or complexity of various learning models or sets of models is examined using VC dimensions. Researchers can learn more about the relative strengths and weaknesses of various models by comparing their VC dimensions.

4) Probably Approximately Correct (PAC) learning: VC dimensions are essential to the PAC learning paradigm. Understanding the trade-off between sample size, model complexity, and generalization performance is made theoretically possible by PAC learning. In PAC learning, sample complexity bounds are derived using VC dimensions.

5) Support Vector Machines (SVMs): In the context of SVMs, a well-liked machine learning approach, VC dimensions are particularly pertinent. The greatest number of points that may be separated by an SVM with no training error is determined by the VC dimension of the SVM. It is crucial to comprehend the generalization characteristics of SVMs.

How VC Dimension Machine Learning Works?

The major ideas and procedures required to better understand how VC dimensions function in machine learning:

1) VC dimensions are linked to hypothesis classes, which are collections of potential models or classifiers that may be discovered by data mining. Hypothesis classes include things like linear classifiers, decision trees, specific-architecture neural networks, etc.

2) The VC dimension assesses a hypothesis class's ability to completely fit or shatter every feasible binary labeling of points. The term "shattering" describes a hypothesis class's capacity to generate every potential label for a given collection of points. A hypothesis class's VC dimension must be at least as large as the largest group of points it may shatter.

3) Binary Labeling: Binary labeling ascribes labels (such as +1 and -1) to specific data points or collections of data points. Finding a model from the hypothesis class that closely resembles the actual labeling of the data is the aim of a learning algorithm.

4) Sample Complexity: A learning algorithm's sample complexity is affected by VC dimensions. Sample complexity is the number of training instances needed for a learning algorithm to perform accurately. In general, the VC dimension of the hypothesis class causes the sample complexity to rise.

5. Generalization Bounds: Using VC dimensions, generalization bounds are derived, and they offer theoretical assurances for the anticipated performance of a learning system on data that is not observed. These limits are influenced by the VC dimension, the size of the training set, and a complexity or capacity metric.

6. Understanding the trade-off between overfitting and underfitting is made easier by using VC measurements. The model may underfit the data and have restricted learning capabilities if the model capacity (defined by the VC dimension) is too low. The model could overfit the training set, on the other hand, and fail to generalize to fresh data if the capacity is too high.

7. Model Selection: By directing the selection of the right model complexity, VC dimensions help in model selection. Depending on the available data and the learning issue, one may choose a model with the appropriate capacity to prevent underfitting or overfitting by taking into account the VC dimensions of various hypothesis classes.

Ways to prove VC Dimensions Machine Learning

i) Definition: Start by outlining what the VC dimension is. A hypothesis class's VC dimension is the most number of points that may be broken by the class, where "shattering" refers to the capacity to give the points any label.

ii) Building a shattered set: one needs to build a set of points that the class can shatter in order to demonstrate that the class has a VC dimension that is at least a particular value. And then establish the bottom bound of the VC dimension by giving a concrete example and proving the class's capacity to label the points with any labels.

iii) Proof of the upper bound: One must demonstrate that no greater group of points can be broken by the hypothesis class in order to prove an upper bound on the VC dimension. Sequential reasoning, probability theory, or geometric arguments are frequently effective in achieving this.

iv) Combinatorial arguments are frequently used to determine how many different divisions (labeling schemes) a hypothesis class is capable of achieving. One can put an upper bound on the VC dimension by demonstrating that the number of divisions increases too slowly or is constrained by the VC dimension.

v) Using fat shattering dimension: A different formulation for the VC dimension is the fat shattering dimension. It indicates an upper constraint on the VC dimension if you can show that a hypothesis class has a fat-shattering dimension of a particular value.

vi) Using Sauer's lemma: The growth function based on the VC dimension has a meaningful bound thanks to Sauer's lemma. You can set an upper bound on the VC dimension by using Sauer's lemma and demonstrating that the growth function is constrained.

Benefits of VC Dimension

Some of the benefits of VC machine learning are:

1. Feature selection and dimensionality reduction are two further applications of the VC dimension. One can find the most informative and appropriate characteristics for a certain learning assignment by calculating the VC dimension of various subsets of features. This decreases the input space's dimensionality and increases the effectiveness and precision of learning algorithms.

2. Analysis of Learning Algorithms: Using VC dimension analysis, researchers may examine how various learning algorithms behave. It offers insights into a learning algorithm's sample complexity or the number of training samples necessary to get a specific degree of generalization performance. Researchers may assess the effectiveness of various learning algorithms by comparing and contrasting them by grasping the link between the VC dimension and sample complexity.

3. Measurement of Model Complexity: The VC dimension offers a way to determine how complicated a model or class of assumptions is. It shows how well the model can match a variety of potential input patterns. More complex relationships in the data can be captured by models with greater VC dimensions. It helps in understanding the wide range and expressive capacity of various models.

Conclusion

 In conclusion, the Vapnik-Chervonenkis (VC) dimension is an important machine learning paradigm with a number of advantages. It functions as an index of model complexity, enabling us to better understand the flexibility and adaptability of various models or assumption classes. It offers theoretical assurances on the performance of generalization, assisting with assessing a model's capacity to generalize from practice data to new data and preventing overfitting. Models with smaller VC dimensions are typically chosen because of their decreased risk of overfitting. This makes the VC dimension valuable for model comparison and selection. By giving academics information on sample complexity and enabling them to evaluate the effectiveness of various algorithms, it also makes it easier to analyze learning algorithms.

Additionally, the VC dimension can help with feature selection and dimensionality reduction, making it easier to identify the features that are most useful for a particular learning job and enhancing the effectiveness and precision of learning algorithms. In general, the VC dimension plays an essential role in understanding the trade-off between model complexity and generalization performance, further assisting in the selection of suitable models, examining learning algorithms, and improving the effectiveness and precision of machine learning systems.