MATLAB Vector
Introduction to MATLAB vector
Vectors are one of the representations of arrays. It tends to be addressed in two different ways line(row) vector and section(column) vector. A vector is defined as enclosed arrangement of components. By utilizing square section we can create vectors in MATLAB.
Defining a vector in MATLAB
MATLAB makes it simpler for you to enter matrices and vectors by providing software packages. A language, intended to look a great deal like the documentation use in direct variable is followed by an interface. We will examine a portion of the essentials of working with vectors in the following tutorial.
A vector is simply defined by a sequence of numeric numbers inside square braces as follows:
>>p = [91] p = 91
If we want to display the vector, typing label is enough to view:
>>p p= 91
If we increment other than one, we have to define the start number, increment value, and the last number.
Let us type an example in command line, a vector that start with 4 and ends in 8 with steps of 0.25 .
p = [4:.25:8] p = Columns 1 through 15 4.0000 4.2500 4.5000 4.7500 5.0000 5.2500 5.5000 5.7500 6.0000 6.2500 6.5000 6.7500 7.0000 7.2500 7.5000 Columns 16 through 17 7.7500 8.0000
Accessing elements within a vector
We can display individual elements in a vector. To access 2st element of a vector we use the following example, executed in MATLAB’s command line.
>>p = [91] p = 91 >>p(2) ans= 9
Note that in the previous example, the outcome isn't shown if we end the line with a semi-colon. When we need to utilize MATLAB to work with enormous frameworks of conditions this will prove to be useful some other time.
MATLAB will permit you to see explicit pieces of the vector. In the event that you need to just gander at the initial three elements in a vector you can utilize a similar documentation to create the vector:
Let’s examine the above statement by executing the right commands to result the desired output.
>>p = [0:2:8] p= 02468 >>p(1:3) ans= 024 >>p(1:2:4) ans= 04 >>p(1:2:4)' ans= 0 4
Vector operations

Addition and subtraction of vectors
We can subtract or add two vectors. The operand vectors involved in the operation must have same number of elements and also same data type to perform the operation.
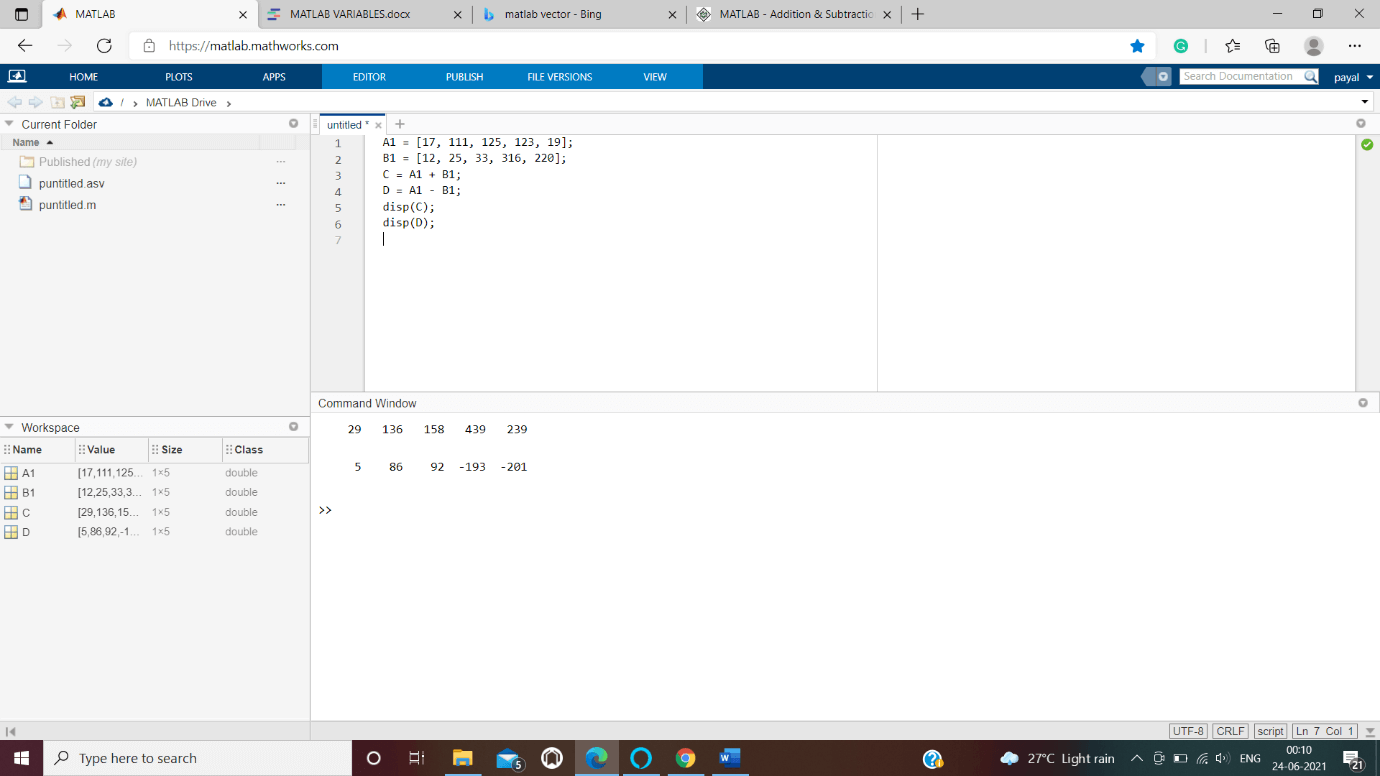
Example: we have created two vectors A1 and B1, to perform the addition and subtraction operation, C and D variables are used to display the results of the operation using disp() function.
A1 = [17, 111, 125, 123, 19]; B1 = [12, 25, 33, 316, 220]; C = A1 + B1; D = A1 - B1; disp(C); disp(D);
Output:
Vectors scalar multiplication
Scalar multiplication:
Scalar multiplication means when we try to multiple a scalar let it be any integer with a vector.
Scalar multiplication produces a same type vector with each element multiplied by the number of original vector.
Example:
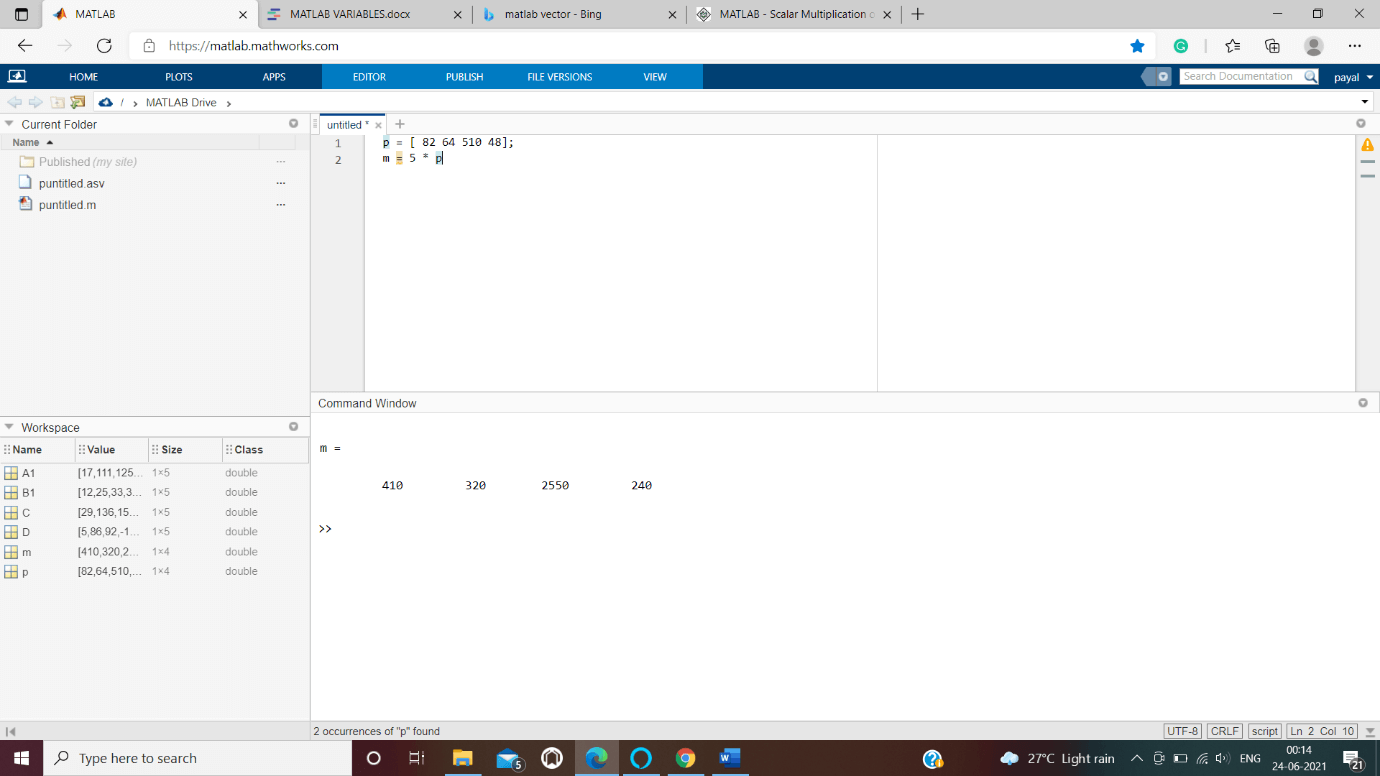
We can run this script file to obtain the output shown in the screenshot.
p = [ 82 64 510 48]; m = 5 * p
Output:
Transpose of a vector
If you want to change a column vector( the vertical vector ) into a row vector(horizontal vector) and vice versa then transpose function can help. This operation is denoted this symbol( ‘ ), which is called as single quote.
Example
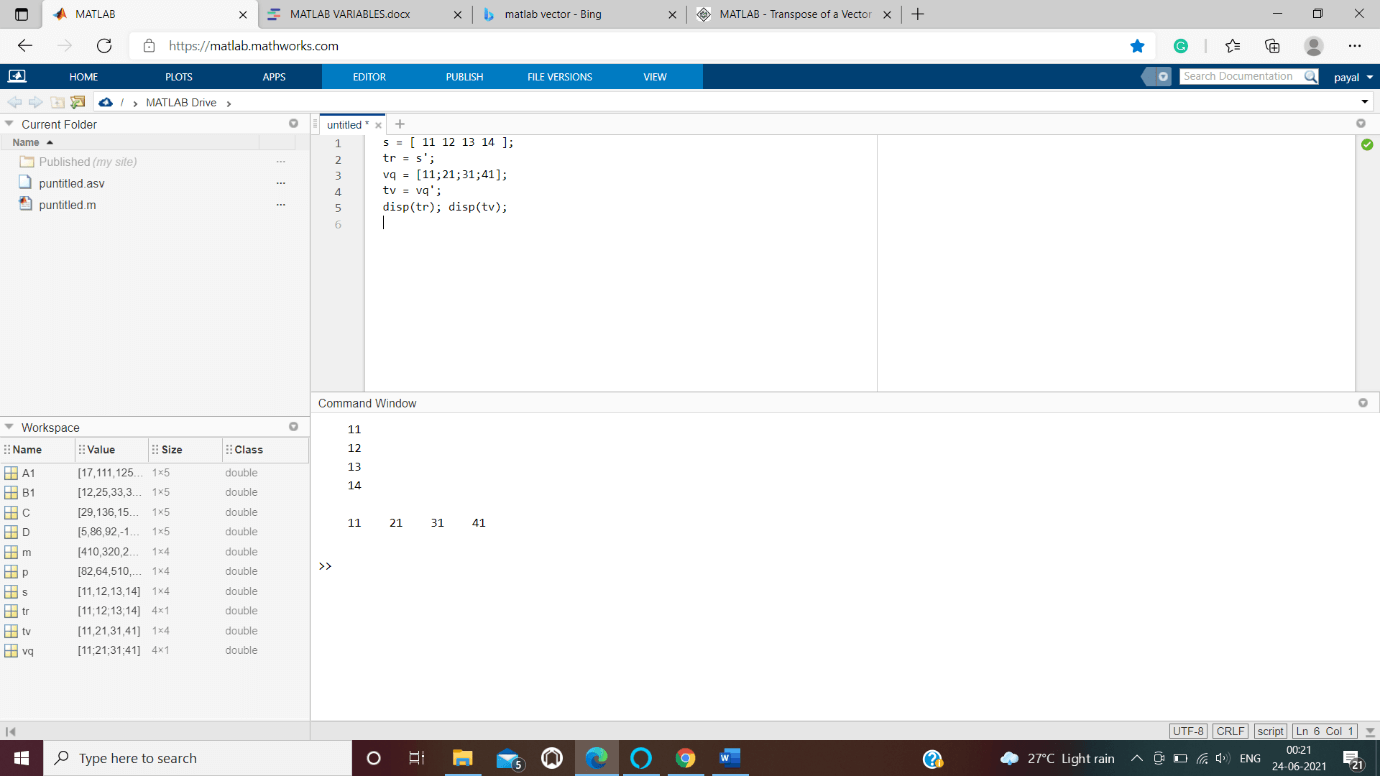
We are creating a script file as follows –
s = [ 11 12 13 14 ]; tr = s'; vq = [11;21;31;41]; tv = vq'; disp(tr); disp(tv);
Output:
Appending vector
To append vectors together we use this append operation provided by MATLAB.
If we have vectors p1 and p2 with n and m number of elements, by appending these vectors, we get new vector ?
p = [p1,p2]
Example:
We have created two vectors p1 and r2, to perform the operation, rMat and cmat variables are used to display the results of the operation.
p is a new combined vector of p1 and p2 vectors.
p1 = [ 11 12 13 14 ]; r2 = [52 62 72 82 ]; p = [p1,r2] rMat = [p1;r2] c1 = [ 12; 22; 32; 43 ]; c2 = [35; 16; 71; 8 ]; c = [c1; c2] cmat = [c1,c2]
Output:
p = 11 12 13 14 52 62 72 82 rMat = 11 12 13 14 52 62 72 82 c = 12 22 32 43 35 16 71 8 cmat = 12 35 22 16 32 71 43 8
Magnitude of a vector
Magnitude of a vector p with elements p1, p2, p3, …,pn, is given by ?
|p| = ?(p12 + p22 + p32 + … + pn2)
Steps to calculate magnitude of a vector as follows:
- A vector ps is produced by multiplying thevector product using (.*) by itself, whose elements are equal to squares of the corresponding elements of vector p as shown below.
- ps = p.*p;
- Now we perform dot product. We get the total value by addition of all elements of vector p by using the sum() function. This sum is obtained and stored in we.
- we= sum(ps);
- To get the magnitude of the vector p, we perform square root of values, use sqrt() function.
- magnitude = sqrt(we);
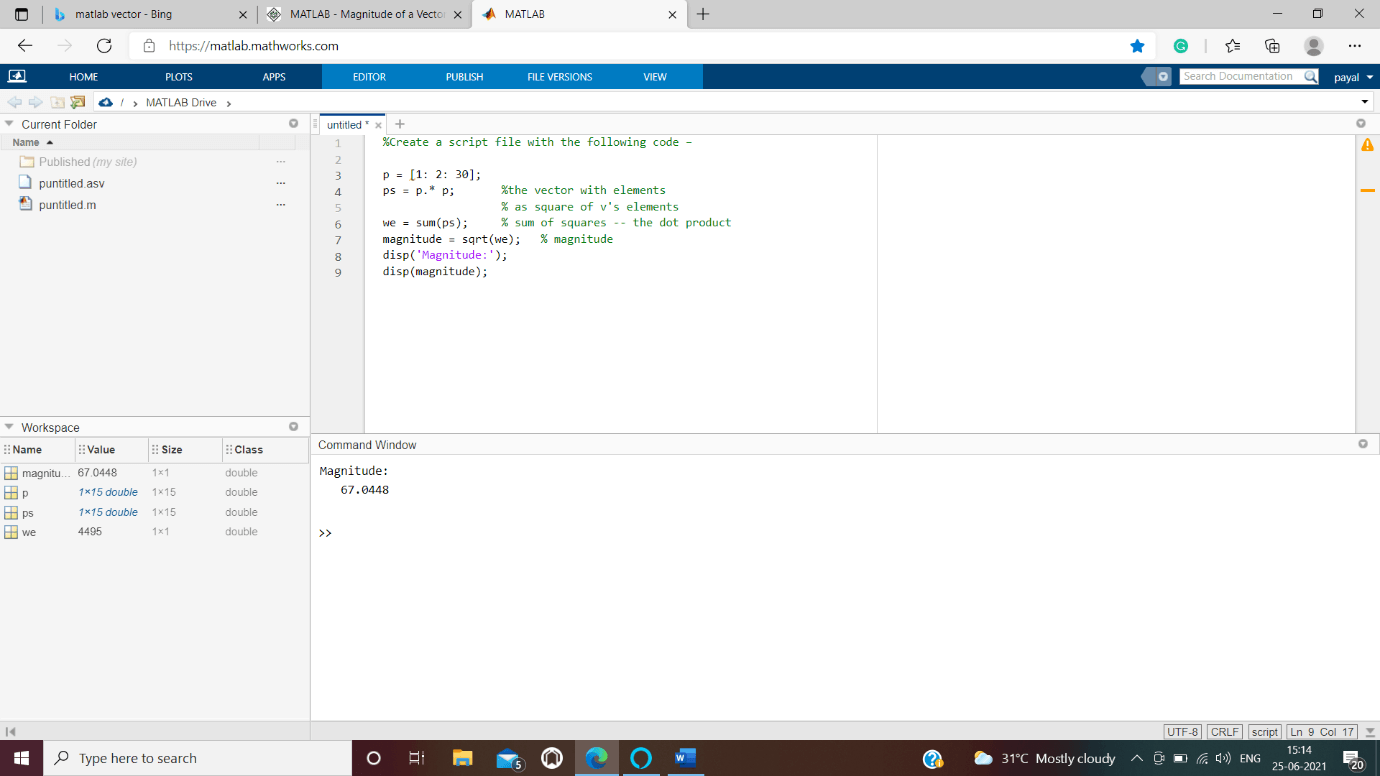
Example:We are creating a script file as follows –the comments embedded in the file explains the performed operations on the matrices.
%we Create a script file as shown below ?
p = [1: 2: 30];
ps = p.* p; %vector with elements
%square of p's elements
we = sum(ps); % sum of elements =contained in ps -- the dot product
magnitude = sqrt(we); % magnitude of “we” elements
disp('Magnitude:');
disp(magnitude);
Output:
Vector dot product
Dot product of two vectors p = (p1, p2, …,pn) and s = (s1, s2, …, sn) is given by ?
p.s = ?(pi.si)
Example:
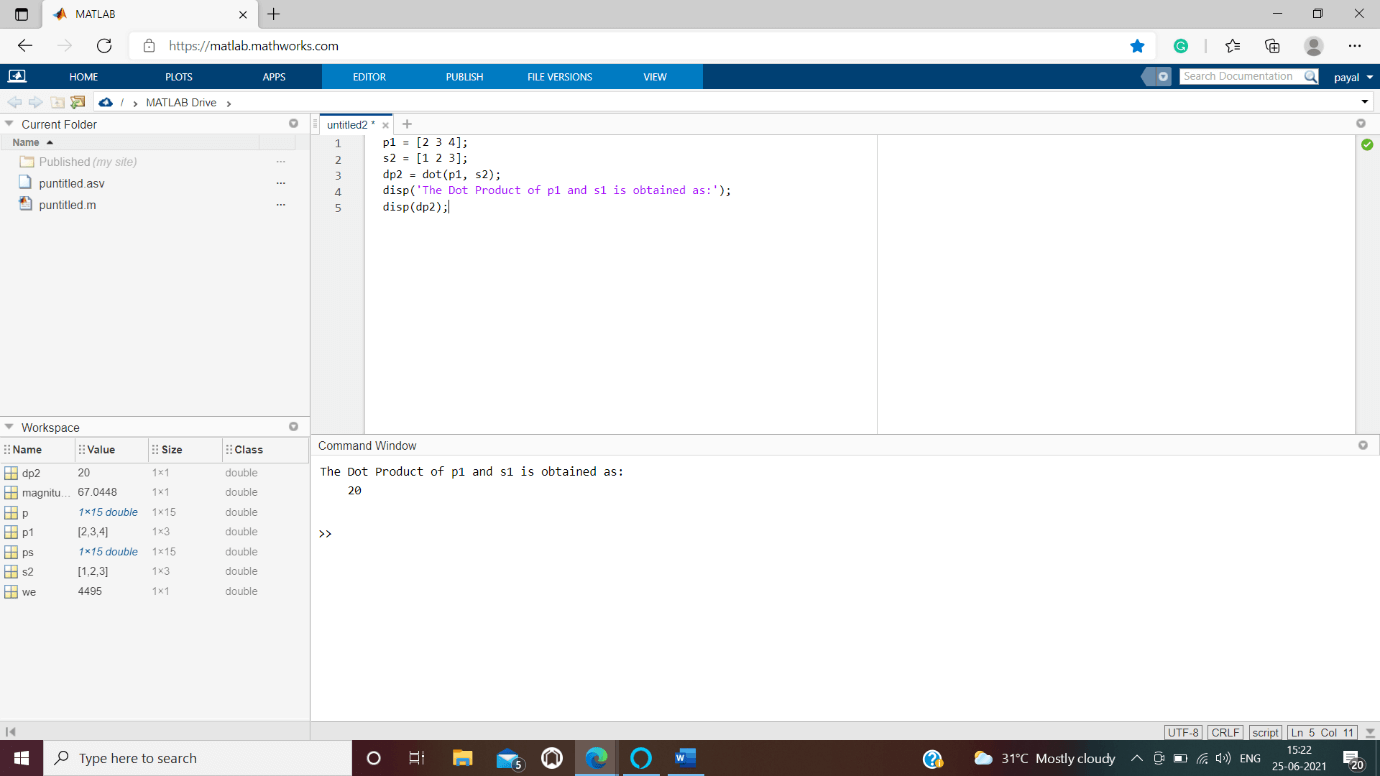
We are creating a script file as follows –
P1 and s1 are two vectors, by using dot() function we are calculating the dot product and therefore displayed the result using disp() function.
p1 = [2 3 4];
s2 = [1 2 3];
dp2 = dot(p1, s2);
disp('The Dot Product of p1 and s1 is obtained as:');
disp(dp2);
Output:
The dot product of p1 and s1 is obtained as: 20
You can also refer the below screenshot for getting a clear understanding.
Uniformly Spaced Elements vector
Uniformly spaced elements vector is created in MATLAB with the help of following syntax.
p = [g : m : l]
The above syntax shows us how to generate a vector p with the parameters:
First element = g
Last element=l
Difference between them=m (any real number)
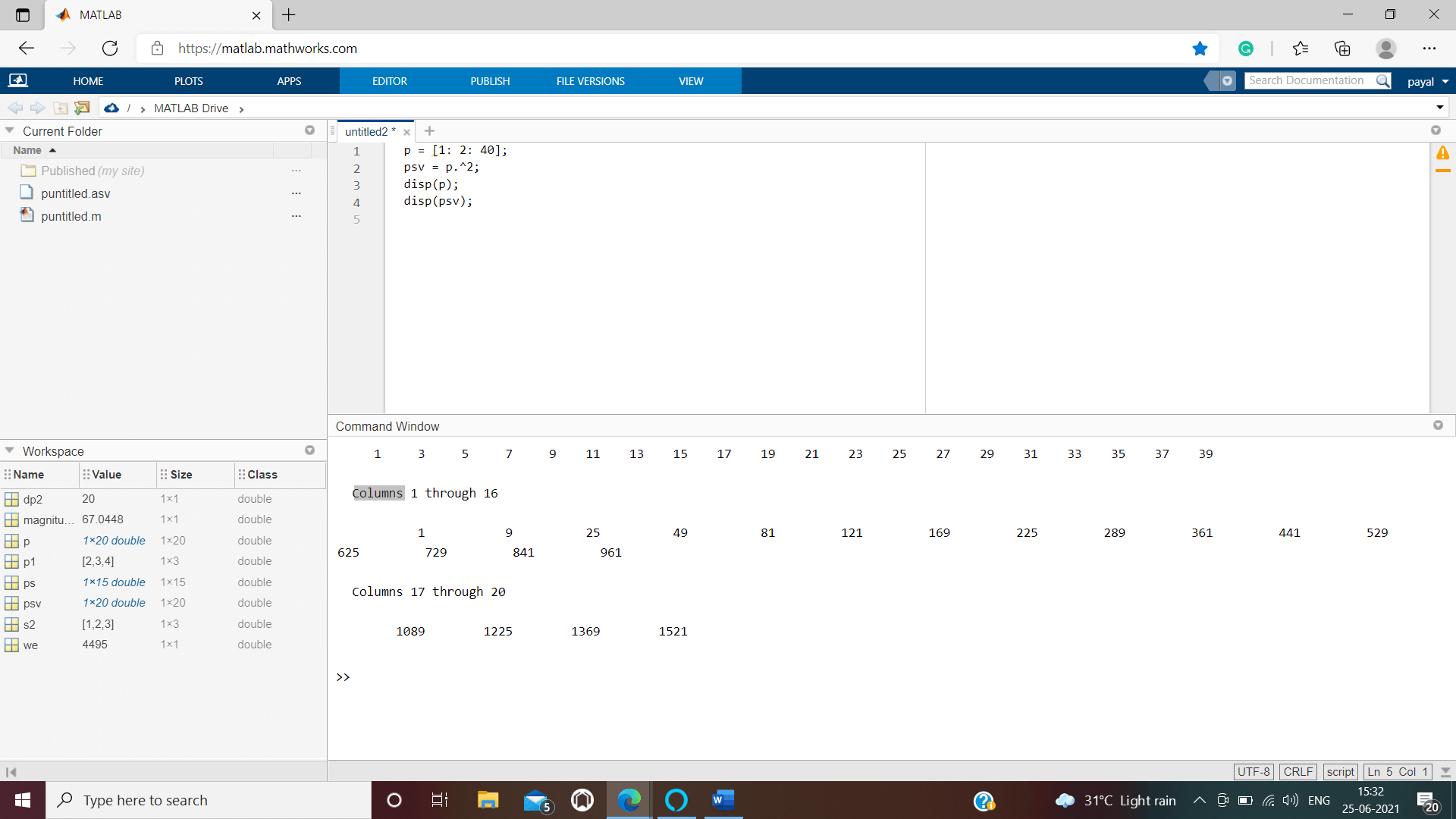
Example: We are creating a script file as follows –
p = [1: 2: 40]; psv = p.^2; disp(p); disp(psv);
Output:
1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 Columns 1 through 16 1 9 25 49 81 121 169 225 289 361 441 529 625 729 841 961 Columns 17 through 20 1089 1225 1369 1521
You can also refer the below screenshot for getting a clear understanding.
Conclusion – Vectors in Matlab
In Matlab, with the help of vectors we can perform multiple logical operations like dot product of two vectors, subtraction of vectors, vector manipulation, finding square root of vector number, power square operation , addition scaling, normal vector multiplication, etc.