2D Shearing

We can denote shearing with ‘SH_x’ and ‘SH_y.’ These ‘SH_x’ and ‘SH_y’ are called “Shearing factor.”

We can perform shearing on the object in two ways-

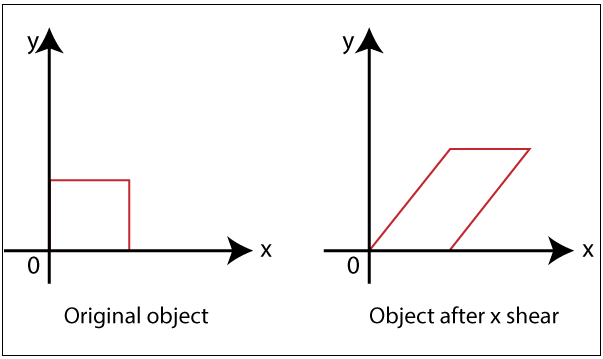
• Shearing along x-axis: In this, we can store the y coordinate and only change the x coordinate. It is also called “Horizontal Shearing.”

We can represent Horizontal Shearing by the following equation-

X₁ = X₀ + SH_x. Y₀

Y₁ = Y₀

We can represent Horizontal shearing in the form of matrix-

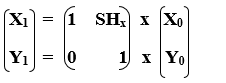
Homogeneous Coordinate Representation: The 3 x 3 matrix for Horizontal Shearing is given below-

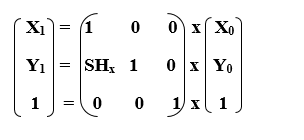
• Shearing along y-axis: In this, we can store the x coordinate and only change the y coordinate. It is also called “Vertical Shearing.”

We can represent Vertical Shearing by the following equation-

X₁ = X₀

Y₁ = Y₀ + SH_y. X₀

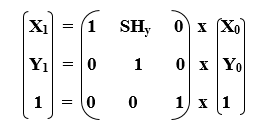
We can represent Vertical Shearing in the form of matrix-

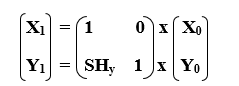
Homogeneous Coordinate Representation: The 3x3 matrix for Vertical Shearing is given below-

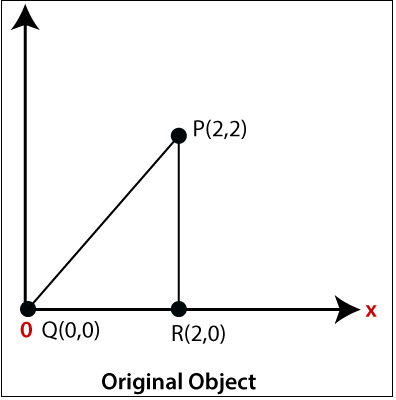
Example: A Triangle with (2, 2), (0, 0) and (2, 0). Apply Shearing factor 2 on X-axis and 2 on Y-axis. Find out the new coordinates of the triangle?     

Solution: We have,

The coordinates of triangle = P (2, 2), Q (0, 0), R (2, 0)

Shearing Factor for X-axis = 2

Shearing Factor for Y-axis = 2

Now, apply the equation to find the new coordinates.

Shearing for X-axis:

For Coordinate P (2, 2)-

Let the new coordinate for P = (X₁, Y₁)

X₁ = X₀ + SH_x. Y₀ = 2 + 2 x 2 = 6

Y₁ = Y₀ = 2

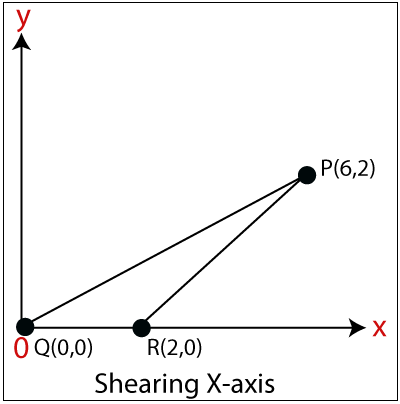
The New Coordinates = (6, 2)

For Coordinate Q (0, 0)-

Let the new coordinate for Q = (X₁, Y₁)

X₁ = X₀ + SH_x. Y₀ = 0 + 2 x 0 = 0

Y₁ = Y₀ = 0

The New Coordinates = (0, 0)

For Coordinate R (2, 0)-

Let the new coordinate for R = (X₁, Y₁)

X₁ = X_­0 + SH_x. Y₀ = 2 + 2 x 0 = 2

Y₁ = Y₀ = 0

The New Coordinates = (2, 0)

The New coordinates of triangle for x-axis = (6, 2), (0, 0), (2, 0)

Shearing for y-axis: 

For Coordinate P (2, 2)-

Let the new coordinate for P = (X₁, Y₁)

X₁ = X₀ = 2

Y₁ = Y₀ + Sh_y.X₀ = 2 + 2 x 2 = 6

The New Coordinates = (2, 6)

For Coordinate Q (0, 0)-

Let the new coordinate for Q = (X₁, Y₁)

X₁ = X₀ = 0

Y₁ = Y₀ +Sh_y. X₀ = 0 + 2 x 0 =0

The New Coordinates = (0, 0)

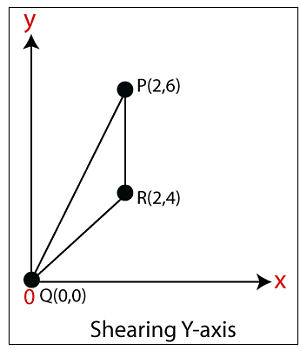
For Coordinate R (2, 0)-

Let the new coordinate for R = (X₁, Y₁)

X₁ = X₀ = 2

Y₁ = Y₀ + Sh_y. X₀ = 0 +2 x 2 = 4

The New Coordinates = (2, 4)

The New coordinates of triangle for y-axis = (2, 6), (0, 0), (2, 4)