Binomial Coefficient Program in C

What is Binomial coefficient?

In the given set of n possibilities, the binomial coefficient(n,k) indicates the order of choosing 'K' results from those possibilities. Binomial coeeficient of posistive n and k is given as:

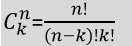
Here n>=k.

Example

Now let's see an example of how this formula works:

Input: B(9,2)

Output:

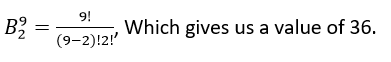
Ways to find Binomial Coeffiecient

There are three ways to find the Binomial coefficient:

• Recursive formula
• Multiplicative formula
• Factorial formula

Now let's use the multiplicative formula to find the binomial coefficient:

#include<stdio.h>


void main() {
    int i, j, n, k, min, c[20][20]={0};
    printf("This program will help us to find the binomial Coefficient" );
    printf("\n Enter the value of n: ");
    scanf("%d", &n);
    printf("\n Enter the value of k: ");
    scanf("%d", &k);
    if(n >= k) {
        for(i=0; i<=n; i++) {
            min = i<k? i:k;
            for(j = 0; j <= min; j++) {
                 if(j==0 || j == i) {
                     c[i][j] = 1;
                 } else {
                     c[i][j] = c[i-1][j-1] + c[i-1][j];
                 }
             }
         }
         printf("%d\t",c[n][k]);
         printf("\n");
     } else {
         printf("\n Invalid input \n Enter value n>=k \n");
     }
}

Output:

Explanation;

The above code is written to find the binomial coefficient of the given value. In the above code, we have taken input from the user using the scanf() function and stored the input into variables n and k. Then we compared both the inputs as we know the condition for finding the binomial coefficient: n should be greater than k. Then the min variable we have declared as an int data type is used to store the minimum value among the two variables, i.e., n and k. Using the for loop, we have to change the value of the 2d array, which we have declared as an integer type. Using the printf statement, we have printed the value in the 2d array.

Using Recursion:

Now let's see how to find the value of the binomial coefficient using the recursion.

Recursion is the process in which the function will call itself.

Code:

#include<stdio.h>
int BC(int n, int k);


int main()
{
        int n,k;
        printf("Enter the values of n and k such that n<k\n");
        printf("Enter the value of n: ");
        scanf("%d",&n);
        printf("Enter the value ok k: ");
        scanf("%d",&k);
        printf("\nBinomial coefficient\n",BC(n,k));
        printf("%d\n",BC(n,k));


        return 0;
}


int BC(int n, int k)
{
        if(k==0 || k==n)
                return 1;
        return BC(n-1,k-1) + BC(n-1,k);
}

Output:

Explanation:

The above code is written to get the binomial coefficient using the recursion. In the above code, we have created a function BC which will return the value of the binomial coefficient. In the main function, we have taken the input from the user such that the n value should be greater than k then we have called the function BC. In the function, k value is checked if the value is equal to zero or equal to n, then 1 will be returned. The BC function will be again called until the values are equal to n or zero. Afterwards, the backtracking process takes place, and the binary coefficient value will be returned. We can see that the values of the traditional and mathematical methods are the same.

Using Factorial

Now, let's see how to calculate the binomial coefficient using the factorial formula

Code:

#include <stdio.h>


int fak(int n) {
    int fak_n=1;
    for(int i=2; i<=n; i++){
        fak_n=fak_n*i;
    }
    return fak_n;
}


int bin(int n, int k) {
    return fak(n) / (fak(k) * fak(n - k));
}
        
int main() {
    int n;
    int k;
    scanf("%d%d", &n, &k);
    printf("%d\n", bin(n, k));
    return 0;
}

Output:

Explanation

The above code is written to print the binomial coefficient. This is the traditional method to find the binomial coefficient. In the above code, we have created a function fak that will return the numbers' factorial. We have created another function, bin() which will call the fak function in the bin function. We have given the formula for finding the binomial coefficient. In the main function, we have taken the values from the user. Then we called the bin function by passing the values. We have called the fak function in the bin function by passing the values using the formula. The fak will return the factorial value.