Tower of Hanoi in C

What is Tower of Hanoi?

The Tower of Hanoi is a gaming problem that was created in 1883 by a French mathematician named Édouard Lucas. The Tower of Hanoi temple in Hanoi, Vietnam, which inspired the name of this puzzle game, was a place of worship.

Three rods and several discs make up the geometric puzzle known as The Tower of Hanoi. The discs are first arranged on a single rod in a cone-like tower structure, stacked one above the other in escalating order of size.

Rules

The goal of this challenge is to transfer the disc stack from the starting rod to another rod while adhering to the following guidelines:

• A single disc can only be moved at once.
• Every move involves taking the top disc from one stack and stacking it on top of another stack; a disc can only be moved if it is the top disc on a stack.
• No disc should be stacked on top of another.

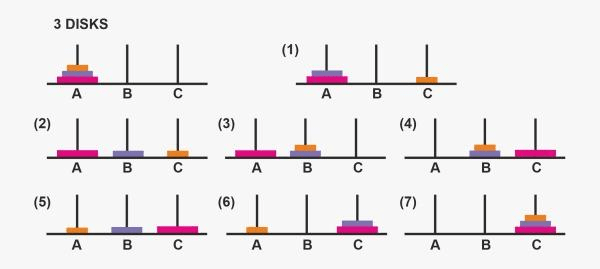
To transfer all of the discs from the leftmost rod to the rightmost rod is the objective. It takes steps to transfer n discs from one rod to another. In order to transfer three discs from the starting rod to the finishing rod, a total of 7 steps are needed. These steps are illustrated in below image:

 Recursive Method Approach

When a function is being executed in a system, recursion is the process through which the function calls itself. When using the recursion approach to address tiny issues, several considerations must be made.

We need to solve this Tower of Hanoi puzzle. Since it has three towers with the names P, Q, and R, the input for this puzzle is 3. This crossword's syntax will be as follows:

#include<stdio.h>
void Tower(int n,char a,char b,char c) {
   if(n>0) {
  	Tower(n-1,a,c,b);
  	printf("%c to %c\n",a,b);
  	Tower(n-1,c,b,a);
   }
}
int main() {
   int n=3;
   Tower(n,'P','Q','R');
}

Program Output

P to Q
P to R
Q to R
P to Q
R to P
R to Q
P to Q

A brief description of this methodology:

Let's use two discs as an illustration:
Tower 1 = 'P', Tower 2 = 'Q', Tower 3 = 'R'.
 
Step 1: Move the first disc from 'P' to 'Q'
Step 2: Move the second disc from 'P' to 'R'
Step 3: Move the first disc from 'Q' to 'R'
 
The pattern is as follows:
 
Transfer 'n-1' discs from 'P' to 'Q'.
Transfer the last disc from 'p' to 'R'.
Transfer 'n-1' discs from 'Q' to 'R'.

C code for the Tower of Hanoi:

#include <stdio.h>
void hanoitower(int n , char P , char R, char Q )
{
	if (n == 1)
	{
    	printf("\n Transfer disc 1 from Tower %c to Tower %c", P, R);
    	return;
	}
	hanoitower(n-1, P, Q, R);
	printf("\n Transfer disc %d from Tower %c to Tower %c", n, P, R);
	hanoitower(n-1, Q, R, P);
}
 
int main()
{
	int n = 4;
	hanoitower(n, 'P', 'R', 'Q'); 
	return 0;
}

Program Output :

 Transfer disc 1 from Tower P to Tower Q
 Transfer disc 2 from Tower P to Tower R
 Transfer disc 1 from Tower Q to Tower R
 Transfer disc 3 from Tower P to Tower Q
 Transfer disc 1 from Tower R to Tower P
 Transfer disc 2 from Tower R to Tower Q
 Transfer disc 1 from Tower P to Tower Q
 Transfer disc 4 from Tower P to Tower R
 Transfer disc 1 from Tower Q to Tower R
 Transfer disc 2 from Tower Q to Tower P
 Transfer disc 1 from Tower R to Tower P
 Transfer disc 3 from Tower Q to Tower R
 Transfer disc 1 from Tower P to Tower Q
 Transfer disc 2 from Tower P to Tower R
 Transfer disc 1 from Tower Q to Tower R

Code Explanation:

In order to start the recursive approach, we first set all the prerequisite information and command lines in C:

In the following line, we have used the Hanoi tower, which in C function, use as a Hanoi function, and void, which is used as the function return type. The function in the command below is stated as "P, Q, and R" because we need to move discs from P to R using Q.

void hanoitower(int n , char P , char R, char Q )

Following the creation of the functions to transfer a disc from P to R, hanoitower(n-1, P, Q, R); is used to move discs from P to Q using R. In these functions, n==1 is a Boolean expression that returns true if n is one and false if n is anything other than 1.

Finally, to move discs from Q to R using P, we utilized hanoitower(n-1, Q, R, P) In these routines, "n-1" denotes the movement of n discs from one tower to another.

 if (n == 1)
	{
    	printf("\n Transfer disc 1 from Tower %c to Tower %c", P, R);
    	return;
	}
	hanoitower(n-1, P, Q, R);
	printf("\n Transfer disc %d from Tower %c to Tower %c", n, P, R);
	hanoitower(n-1, Q, R, P);

This was a succinct explanation of the Tower of Hanoi's recursive approach in C, and we also included a detailed description of why it is necessary to swap the tower names' locations in codes in order to get the desired outcome.