C Program for Extended Euclidean algorithms

The Euclidean method simply computes the GCD (greatest common divisor) of two numbers, p and q. (Let's assume)

The GCD of two integers is the greatest number that divides them both. GCD may be calculated simply by factorizing both integers and multiplying common factors.

The expanded version additionally discovers a way to express GCD in terms of p and q, i.e., coefficients i and j, for which:

(p * i) + (q*j) = gcd(p,q)

It is important to remember that we can always discover such a depiction.

Extended Euclidean Algorithm (EEA) using the C language

In this part, we will use the letter "h" to represent the GCD of p and q. The modifications to the original method (algorithm) are straightforward. If we remember the procedure, we can observe that it concludes with p = h and q = 0. We may readily derive coefficients for these parameters, namely (h * 10) + (0 * 0) = h

We may continue to backtrack the repetitive calls, starting with these coefficients (i, j) = (10, 0)

All that remains is to determine how the coefficients i and j change throughout the transition from (p, q) to (q, p mod q).

Assume that we have the coefficients (i₁, j₁) for (q, p mod q):

(q * i­1 )­­+ ((p mod q) * j­1 ) = h

We wish to obtain the (i, j) pair for (p, q):

p * i + q * j = h

(p mod q) can be represented as:

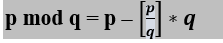
Substituting this expression into the (i₁, j₁) coefficient equation yields:

Pseudo Code for the Extended Euclidean Algorithm (EEA):

function Gcd_Extended(p, q)
    a<- 0;    old_a <- 1
    b <- 1;    old_b <- 0
    c <- q;    old_c <- p
    while c ? 0
        quotient <- old_c div c
        (old_c, c) <- (c, old_c - quotient * c)
        (old_a, a) <- (a, old_a - quotient * a)
        (old_b, b) <- (b, old_b - quotient * b)       
    output "Bézout coefficients:", (old_a, old_b)
    output "greatest common divisor:", old_c
    output "quotients by the GCD:", (b, a)

Example 1:

This program code shows the Extended Euclidean Algorithm (EEA) in the C programming language using the Recursive Method.

/* C program code to show the operation of an Extended Euclidean Algorithm (EEA)*/
#include <stdio.h>


/* Extended Euclidean Algorithm (EEA) C Function */
int Gcd_Extended(int p, int q, int* i, int* j)
{
	/* Base Condition for EEA */
	if (p == 0) 
	{
		*i = 0;
		*j = 1;
		return q;
	}


	int i1, j1;  /* To save the result of the recursive call function */ 
	int Gcd_E = Gcd_Extended(q % p, p, &i1, &j1);


	/* Using the results of the recursive call, update the values of i and j */
	*i = j1 - (q / p) * i1;
	*j = i1;


	return Gcd_E;
}


/* main() function block */
int main()
{
	int i, j;
	int p = 18, q = 63;
	int h = Gcd_Extended(p, q, &i, &j);
	printf("The GCD of two numbers (%d, %d) = %d", p, q, h);
	return 0;
}

Output:

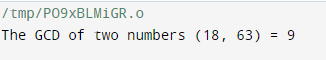
Auxiliary Space of EEA : O(1)

Time Complexity of EEA : O(log min(p, q))

This extended Euclidean algorithm implementation yields proper answers for negative numbers as well.

Example 2:

This program code shows the Extended Euclidean Algorithm (EEA) in the C language using the Iterative Method.

#include<stdio.h>
int Gcd_Extended(int,int);
int main()
{
	int p,q;
	int Gcd_E;
	printf("Enter the first number: ");
	scanf("%d",&p);
	printf("\nEnter second number:");
	scanf("%d",&q);
	
	Gcd_E=Gcd_Extended(p,q);
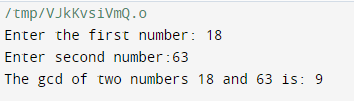
	printf("The gcd of two numbers %d and %d is: %d",p,q,Gcd_E);
	
	return(0);
	
}
int Gcd_Extended(int p,int q)
{
	int r;
	if(p==0)
	{
		return(q);
	}
	
	else if(q==0)
	{
		return(p);
	}
	
	else
	{
		while(q!=0)
		{
			r=p%q;
			p=q;
			q=r;
		}
		return(p);
	}
}

Output:

When p and q are coprime, the extended Euclidean method comes in handy (or the gcd is 1). Because i is the mod multiplicative inverse of "p modulo q," and j is the mod multiplicative inverse of "q modulo p." The calculation of the modulo inverse, in particular, is a critical step in the RSA public-key encryption scheme.