Pascal Triangle in C
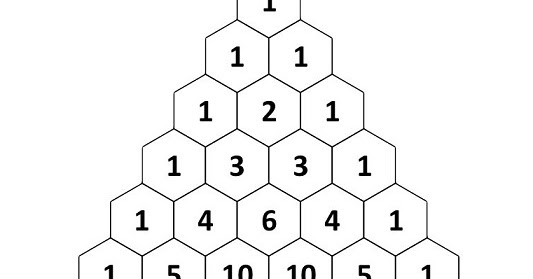
- The pascal triangle in c is an array of binomial coefficients in triangular form. Here the nth row contains the binomial coefficient of ncr.
- In a pascal triangle, every number is obtained by summing the two numbers above it.
Example:

- There are two different ways to obtain the pascal triangle in c, They are
- Using 2d array
- Using combination
Using 2d Arrays
- Here every number is the sum of the above two numbers, To store the values obtained, we create a 2d array.
- To obtain a value,we use stored values from the array.
- The time complexity for generating the pascal triangle is O(n2).
- The space complexity for generating the pascal triangle is O(1).
Program:
/ / program to print pascal triangle
/ / using 2d array method
#include <stdio.h>
/ / pascal function
Void pascal ( int n )
{
/ / defining a array to store
Int a [n] [n];
for ( inti = 0 ; i< n; i++)
{
for ( int j = 0;j <= i; j++)
{
If ( i == j | | j == 0)
a [i] [j] = 1;
else
a [i] [j] = ( a [i -1][j – 1] + a [i -1][j];
printf(“%d ” , a [i][j] );
}
Printf( “\n” );
} }
/ / main method
int main ( ) {
int n = 5;
pascal (n);
return 0;
}
Output:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
2. combination method:
- In this method, C(n,r) is used to represent the nth row of nth element in pascal triangle.
- The formula to calculate is :
C(n,r) = C(n, r - 1) * (n – r + 1 ) / r
Program:
#include <stdio.h>
Void pascal ( int n )
{
for ( inti = 1;i <= n;i++)
{
Int c = 1;
for ( int j = 1; j <= i; j++ )
{
Printf( “ %d ”, c);
c = c * (i – j) / j;
}
Printf(“ \n”); } }
/ / main method
int main ( ) {
int n = 5;
pascal (n);
return 0;
}
Output:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
- Here the element in the pascal triangle is calculated in O(1) time using the above formula.
- The time complexity for generating the pascal triangle is O(n2).
- The space complexity for generating the pascal triangle is O(1).