Two-Dimensional array in C
What is an Array?
The collection of a fixed number of elements of homogeneous data types that are stored in contiguous locations in the memory is known as an array. Only a fixed number of values can be stored in an array. Therefore an array of integer data types can only store values with an integer data type.
It is a type of data structure that only stores elements that are of the same data type as the array. These elements are stored in continuous memory locations. A given direction in which the elements of an array can vary is called as its dimension.
For example, an array of strings refers to a collection of strings stored in a single array.
There are two types of arrays: single dimension arrays and multi-dimensional arrays.
Single Dimension Arrays
An array that contains a single dimension is called a single-dimensional array.
Multi Dimension Arrays
Unlike a single-dimensional array, a multi-dimensional array is an array that contains more than one dimension. A two-dimensional array is also a multi-dimensional array that has two dimensions, and it is also called as an array of arrays.
We can think of a two-dimensional array as a matrix that contains a given number of rows and columns.
Following is an example of a two-dimensional array:
| 1 | 2 | 3 |
| 4 | 5 | 6 |
The above two-dimensional array has two rows and three columns.
Zero-based indexing is followed by a two-dimensional array in C, just like all other arrays in C.
In order to understand a two-dimensional array, we should have an understanding of its syntax and its representation.
Example of a two-dimensional array:
int array[2][3]={{1,2,3},{4,5,6}};
In the above example, a two-dimensional array with two rows and three columns has been defined with the values as shown in the above table.
Syntax:
data_typearray_name[i][j]
Here, data_type is the type of data to be stored in the array, and i and j are the size of its two dimensions, i denotes the rows, and j denotes the columns.
Initializing a Two-Dimensional Array in C
There are two methods through which we can initialize an array. These two methods are given below:
Method 1: This method is used to initialize the array without using any nested braces:
int array[i][j]={element 1, element 2, ……..element ij};
Through the above syntax, we can create an array of size i*j, and its elements will be filled in the following manner:
The first row will be filled left to right by the first j elements. Then j+1 onward, the next y elements on the second row will be filled from left to right. Like this, one after the other, all the x rows will be filled.
An example of this method:
int arr[2][3]={3,4,5,8,9,2};
With the above initialization, we will have an array of sizes 2*3.
Method 2: This method makes it easier to visualize each of the rows and columns. In this method, the two-dimensional array is initialized using the nested braces.
int arr[i][j]={{element 1, element 2, .. element j} , {..}, {.., element ij-1, elementij}};
Here, each nested brace represents a single row, with the order of the elements in our two-dimensional array's columns being from left to right.
Accessing Elements in a Two-dimensional Array
Indices are required in a two-dimensional array, just like a single-dimensional array, in order to access the necessary elements. Accessing a specific element requires a row and column index. To print a two-dimensional array for nested loops, two indices are required, one to traverse the rows, and the other to traverse the columns in each row.
#include <stdio.h>
int main()
{
// array declaration and initialization
int arr[4][3] = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}, {10, 11, 12}};
// accessing and printing the elements
for ( int i = 0; i < 4; i++ ) {
// variable i traverse the rows
for ( int j = 0; j < 3; j++ ) {
// variable j traverses the columns
printf("arr [%d][%d] = %d\n", i,j, arr[i][j] );
}
}
return 0;
}
Output:
arr [0][0] = 1
arr [0][1] = 2
arr [0][2] = 3
arr [1][0] = 4
arr [1][1] = 5
arr [1][2] = 6
arr [2][0] = 7
arr [2][1] = 8
arr [2][2] = 9
arr [3][0] = 10
arr [3][1] = 11
arr [3][2] = 12
The above code depicts how to access a two-dimensional array in a C program.
How to store data entered by user in a two-dimensional array?
The number of elements that a two dimensional array can have can be computed by utilizing thefollowing formula:
There can be i*j elements in the array a[i][j]. This means that the numbers of elements present in the given array can be calculated by its indexes. Now, let us take an example,
#include<stdio.h>
int main(){
//Two-dimensional array declaration
int arr[3][3];
for(int i=0;i<3;i++){
for(int j=0;j<3;j++){
printf(“Enter the values for the array index [%d][%d]:”,i,j);
scanf(“%d”,&arr[i][j]);
}
}
//Now, Displaying the values entered by the user in the array.
printf(“Elements of the two-dimensional array:\n”);
for(i=0;i<3;i++){
for(j=0;j<3;j++){
printf(“%d \t”,arr[i][j]);
}
printf(“\n”);
}
return 0;
}
Output:
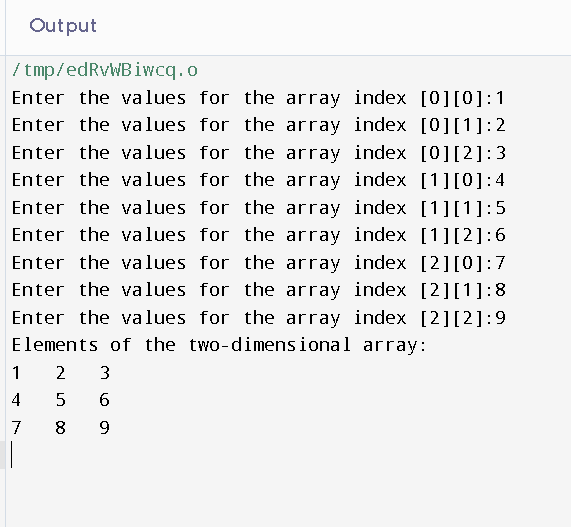
In the above example, the array we have has three dimensions. The term "subscripts" refers to these dimensions. The first subscript value in this array is 3, and the second subscript value is also 3.
As a result, the array arr[3][3] can contain 9 elements.
Here, two for loops are being used to store the values entered by the user, one of them is a nested loop. In the outer loop, the first loop runs from 0 to the first subscript-1, and in the inner loop, the second loop runs from 0 to the second subscript-1.
We can also let the user define the size of the array by taking two integer inputs and using them to define the array: int a[n1][n2]
The actual representation of the array in the memory would be as shown below:
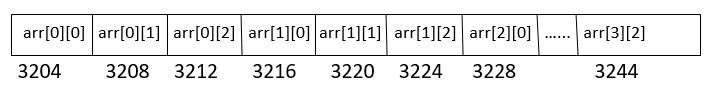
Because the array is of the integer type, each element would require four bytes, which is why the addresses of the elements differ by four. Hex is typically used to represent the addresses. You can see that the address difference between each element is equal to the size of one element (int size 4), which indicates that the elements are stored in contiguous locations.
Two dimensional Arrays and Pointers
We already know that the name of a one-dimensional array serves as a pointer to the base element, the first element of the array. However, the logic is slightly different for 2D arrays. A collection of multiple one dimensional arrays constitutes a 2D array. A two dimensional array of pointer can be created as shown below:
Int *arr[i][j];
//creates a two dimensional integer pointer array with i rows and j columns
The actual address representation ought to be in hex, so we use %p rather than %d. This is only done to show that the elements are stored in memory locations that are adjacent to one another. The difference between these addresses is actually the number of bytes used by the elements of that row.
Calculate the address of a two dimensional array element
In order to determine the address of an element in a two dimensional array, there are two methods:
1. Row Major Method
2. Column Major Method
1. Row Major Method
The address of a random element, arr[i][j], can be calculated if an array is represented by arr[x][y], where x represents the rows and y represents the columns.
The address of element arr[0][0] (the first element of the array) is represented by the Base Address plus (i * y + j) * size in this case.
Address array[i][j]= Base Address + (i*y+j) * Size
Let us take an example. An array is given array[15][20] with a base address of 150 and a memory size of 4 bytes for each element. Using row major method, find the address of array[9][6].
Address of array[9][6] = Base Address + (9*20 + 6)*4
= 150 + (184+6)*4
= 150+744 = 894
2. Column Major Method
Using the column major method, the address of a random element can be calculated as follows if an array is represented by arr[x][y], where x represents the rows and y represents the columns:
The base address plus (j * x + i) * size is the address of arr[i][j].
Now, let us take an example. An array (array[18][18]) is given with a base address of 150 and a 4 bytes size of memory. Using Column major method, find the address of array[3][14].
Address of arr[3][14] = Base Address + (j * x + i) * size
= 150 + (14*18+ 3)*4
= 150+ 255*4
= 150+ 1020 = 1170