LCM of two numbers in C

LCM is a mathematical term which stands for Least Common Multiple. LCM of any two numbers is the smallest positive value(number) which is evenly divisible by the two given numbers.

Consider a and b as two numbers and L denotes the LCM of a and b.

Now, if a=4 and b=6

Then, L will be the smallest number which is divisible by both a and b, i.e., 4 and 6, without leaving any remainder.

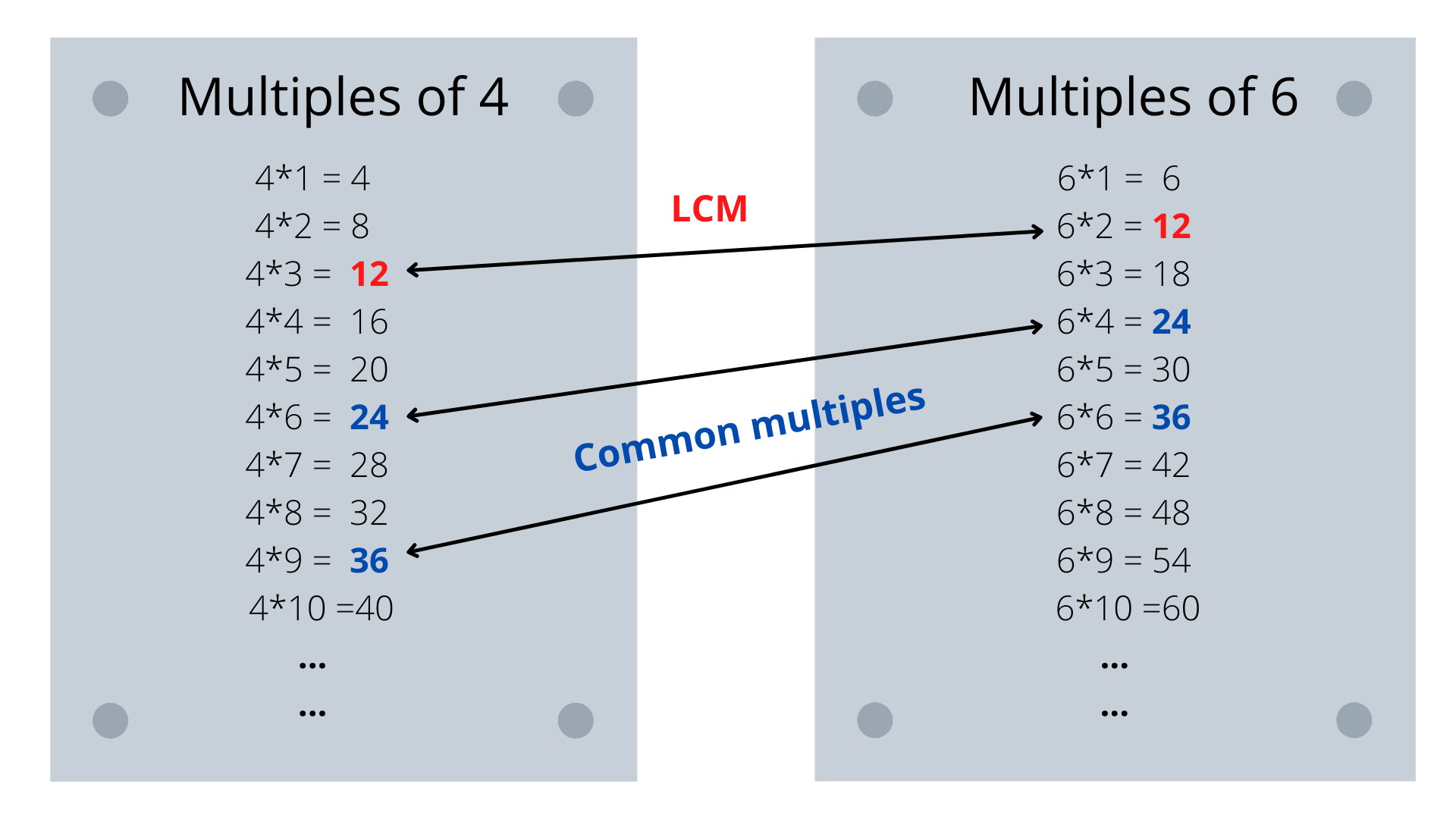
                                    Figure 1 :  Finding the common multiples of 4 and 6

There are various ways to find LCM of two numbers, some of them are as follows:

1. Prime factorization
2. Euclidean algorithm
3. Listing method ( figure 1)

Algorithm of LCM

The mathematics behind to find the LCM of two numbers can be deduced to an algorithm:

1) Initialize the variables a and b.

2) Store the common multiples of a and b into the variable L.

3) Check whether L is divisible by both a and b.

4) If step 3 is true, display L as the LCM of two numbers (a and b).

5) Else, increase the value of L, and go to step 3.

6) Halt the program.

Finding LCM of two numbers using C programming

Before getting our hands dirty with the coding part, let’s try to deduce the logic behind this mathematical concept.

Consider the same set of examples discussed earlier, where L was the LCM of two numbers a and b.

? L is the smallest number divisible by a and b.

Now, if we think about the logical part (in C code) which will result in our output, the range L will lie between 1 to a*b (product of a and b). Here we are considering the base case to denote the range of L.

i.e.,   L = 1 to L = a*b                                   - (i)

Also, from Step 3 of the algorithm:

      ( L%a == 0 && L%b==0)                     - (ii)

Program 1

int main()
	{
	
	int a,b,L;   // declaring variables


	printf("Enter two numbers");
	
	scanf("%d %d", &a,&b);


	for( L=1; L<= a *b ; L++)              //from statement (i)


	    if( L%a==0 && L%b==0)	         //from statement (ii)
	    break;


	printf("LCM is %d", L);
	
	}

Output:

Program 2: LCM of two numbers using GCD

Here, we will follow a basic formula to find the LCM of two numbers a and b.

The formula is as follows:

LCM(a,b) = (a*b) / GCD

*GCD stands for Greatest Common Divisor. The GCD is the largest integer which will divide each of the given numbers evenly.

Let’s understand this using C programming:

int main()
     {
          int num1, num2, lcm, temp, gcd;  //declaring the variables


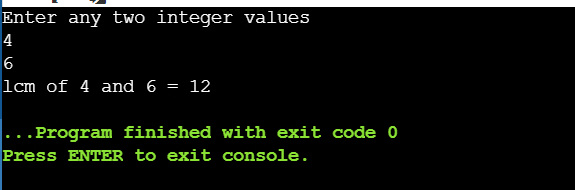
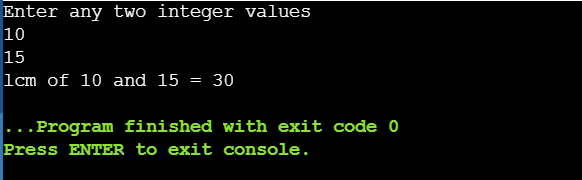
    	printf("Enter any two integer values \n");
    	scanf("%d %d", &num1, &num2);


 	   int a = num1;
    	   int b = num2;
    
    	while (num2 != 0) 
{
 	temp = num2;                             // storing the output values in temp variable
 	num2 = num1 % num2;
 	num1 = temp;
           }
         gcd = num1;
         lcm = (a * b) / gcd;
         printf("lcm of %d and %d = %d", a, b, lcm);
         return 0;


      }

Output: 

Program 3: LCM of two numbers using function

int fun_lcm(int a,int b);                      // function declaration   
 int main()  
{  
    int num1, num2, lcm;
    printf ("Enter any two numbers :\n");  
    scanf ("%d %d", &num1, &num2);  
    lcm = fun_lcm( num1, num2);      // function calling  
    printf ( " \n LCM of %d and %d is %d. ", num1, num2, lcm);  
    return 0;  
}  
  
int fun_lcm ( int num1, int num2)   // function definition   
{  
    static int max = 1;  
    if ( max % num1  == 0 && max % num2 == 0)  
    {  
        return max;  
    }  
    else  
    {  
        max++;  
        fun_lcm( num1, num2);  
        return max;  
    }
  } 

Output:

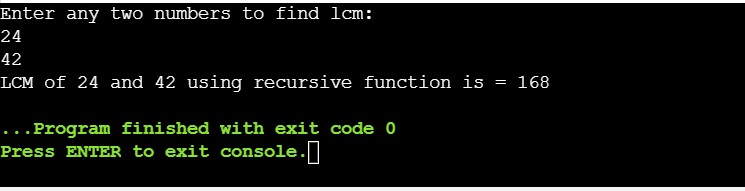
Program 4: LCM of two numbers using recursion

int lcm(int a, int b);


int main()
{
    int num1, num2, LCM;


    /* Input two numbers from user */


    printf("Enter any two numbers to find lcm: ");
    scanf("%d%d", &num1, &num2);
    
    
    if(num1 > num2)
        LCM = lcm(num2, num1);
    else
        LCM = lcm(num1, num2);
        
    printf("LCM of %d and %d using recursive function is = %d", num1, num2, LCM);
    
    return 0;
}


//Recursive function to find lcm of two numbers 'a' and 'b'.


int lcm(int a, int b)
{
    static int multiple = 0;
    
    /* Increments multiple by adding max value to it */


    multiple += b;
    


     // Base case of recursion or recursive function


    if((multiple % a == 0) && (multiple % b == 0))
    {
        return multiple;
    }
    else 
    {
        return lcm(a, b);
    }
}

Output: