Difference between Permutation and Combination

Permutation

The permutation is an action of arranging all or a few members of a set within a linear order. In other words, it is a selection process in which sequence matters. If a set is already in sequence, then the rearrangement of its elements is called the process of permuting.

For instance: the permutations of the numbers in a small set {1, 2, 3} are:

(1,2,3), (1,3,2), (3,1,2), (3,2,1), (2,3,1), (2,1,3)

Formula:

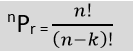
Here,

n= is the total number of elements in a set.

r= the number of selected objects

!= factorial

Combination

The combination is a way of selecting a given number of elements from a bulk collection without regard of their arrangement. In other words, in combination, items can be selected in any order.

Formula:

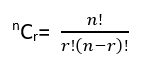
Here,

n= is the total number of elements in a set.

r= the number of selected objects (the order does not matter)

!= factorial

Comparison between permutation and combination

Basis	Permutation	Combination
Meaning	A permutation is an action of arranging all or a few members of a set within a linear order.	The combination is a way of selecting a given number of elements from a bulk collection without regard to their arrangement.
Order	In permutation, order of the elements is necessary.	In combination, order of the elements is not necessary.
Formula	permutation formula is: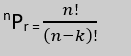	Combination formula is: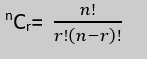
Denotes	Permutation denotes several ways to arrange things, people, digits, alphabets, colors, etc.	Combination denotes several ways of selecting menu items, food, clothes, subjects, etc.