Logo
×

Bigint (BIG INTEGERS) in C with Example

The maximum number of digits that a long, long int can have in C/C++ is 20. The issue is how to store the 22-digit number, which is difficult to do with any simple type. Therefore, let's create a new data type called BigInt to address this type of problem. A few fundamental operations are applied to the new data type in this article.

  1. Adding two large numbers
  2. Subtracting two large numbers
  3. Multiplying two large numbers
  4. Divide two significant digits.
  5. Two large integers modulo
  6. Increase a large number by one.
  7. a large integer's square root
  8. To determine which is greater and which is smaller, compare two large integers.
  9. Determine the huge integer's digit count.
  10. Show the large integer.
  11. Make a huge integer from an integer.

Applications of BigInt

Here are some straightforward uses for the new BigInt data type:

  1. Calculating a large number's Fibonacci number.
  2. Calculating a huge integer's Catalan number.
  3. Calculating a large integer's factorial.

Approach

The features listed below are being implemented to produce a big new integer data type:

  1. Using C++ strings, we can store very large numbers as well because we can save our numbers as characters (in reverse order for efficiency).
  2. Use the fundamentals of addition to add or remove two large integers, which states to add the corresponding two digits and, if any carry is produced, to add it to the sum of the subsequent digits. Repeat this process until all digits have been added or subtracted.
  3. Like this, when multiplying two numbers, follow the basic mathematical procedure, which dictates to multiply each digit of one number by the other entire number before adding all the results.
  4. On BigInt, the following operations are being carried out:
    • Defining a few large integers
    • Examining the huge integer's digit count.
    • Decrementation, Post-Incrementation, or Both
    • Two large integers are added.
    • Taking away two large integers.
    • Two large integers being multiplied.
    • Split two significant digits of two large integers modulo
    • A large integer's square root (floor integer value)
    • Increase a large number by one.
    • Transforming a little integer into a large integer.
    • Fibonacci calculations up to 10,000. even 100,000 but more slowly
    • Factorial calculations up to 1000.
    • Catalan computation up to 1000.
    • Comparing the bigger and smaller big integer.

The above method is implemented in C++ as follows:

// C++ programme to put the aforesaid strategy into practise.
#include <bits/stdc++.h>
 
usingnamespacestd;
 
classBigInt{
    string digits;
public:
 
    BigInt(unsigned longlong n = 0);
    BigInt(string &);
    BigInt(constchar *);
    BigInt(BigInt &);
 
    //Helping Roles:
    friendvoid divide_by_2(BigInt &a);
    friendboolNull(const BigInt &);
    friendintLength(const BigInt &);
    intoperator[](constint)const;
 
               /* * * * Operator Overloading * * * */
 
    //Direct responsibility
    BigInt &operator=(const BigInt &);
 
    //Post/Pre-Incremental Calculation
    BigInt &operator++();
    BigInt operator++(int temp);
    BigInt &operator--();
    BigInt operator--(int temp);
 
    //Subtraction and Addition
    friend BigInt &operator+=(BigInt &, const BigInt &);
    friend BigInt operator+(const BigInt &, const BigInt &);
    friend BigInt operator-(const BigInt &, const BigInt &);
    friend BigInt &operator-=(BigInt &, const BigInt &);
 
    //operators for comparison
    friendbool operator==(const BigInt &, const BigInt &);
    friendbooloperator!=(const BigInt &, const BigInt &);
 
    friendbool operator>(const BigInt &, const BigInt &);
    friendbool operator>=(const BigInt &, const BigInt &);
    friendbool operator<(const BigInt &, const BigInt &);
    friendbool operator<=(const BigInt &, const BigInt &);
 
    //Division and Exponentiation
    friend BigInt &operator*=(BigInt &, const BigInt &);
    friend BigInt operator*(const BigInt &, const BigInt &);
    friend BigInt &operator/=(BigInt &, const BigInt &);
    friend BigInt operator/(const BigInt &, const BigInt &);
 
    
    friend BigInt operator%(const BigInt &, const BigInt &);
    friend BigInt &operator%=(BigInt &, const BigInt &);
 
    
    friend BigInt &operator^=(BigInt &,const BigInt &);
    friend BigInt operator^(BigInt &, const BigInt &);
     
    //Function with Square Roots
    friend BigInt sqrt(BigInt &a);
 
    
    friendostream&operator<<(ostream&,const BigInt &);
    friendistream&operator>>(istream&, BigInt &);
 
    
    friend BigInt NthCatalan(int n);
    friend BigInt NthFibonacci(int n);
    friend BigInt Factorial(int n);
};
 
BigInt::BigInt(string & s){
    digits = "";
    int n = s.size();
    for (inti = n - 1; i>= 0;i--){
        if(!isdigit(s[i]))
            throw("ERROR");
        digits.push_back(s[i] - '0');
    }
}
BigInt::BigInt(unsigned longlong nr){
    do{
        digits.push_back(nr % 10);
        nr /= 10;
    } while (nr);
}
BigInt::BigInt(constchar *s){
    digits = "";
    for (inti = strlen(s) - 1; i>= 0;i--)
    {
        if(!isdigit(s[i]))
            throw("ERROR");
        digits.push_back(s[i] - '0');
    }
}
BigInt::BigInt(BigInt & a){
    digits = a.digits;
}
 
boolNull(const BigInt& a){
    if(a.digits.size() == 1 &&a.digits[0] == 0)
        returntrue;
    returnfalse;
}
intLength(const BigInt & a){
    returna.digits.size();
}
intBigInt::operator[](constint index)const{
    if(digits.size() <= index || index < 0)
        throw("ERROR");
    return digits[index];
}
bool operator==(const BigInt &a, const BigInt &b){
    returna.digits == b.digits;
}
booloperator!=(const BigInt &a,const BigInt &b){
    return !(a == b);
}
bool operator<(constBigInt&a,constBigInt&b){
    int n = Length(a), m = Length(b);
    if(n != m)
        return n <m;
    while(n--)
        if(a.digits[n] != b.digits[n])
            returna.digits[n] <b.digits[n];
    returnfalse;
}
bool operator>(constBigInt&a,constBigInt&b){
    return b <a;
}
bool operator>=(constBigInt&a,constBigInt&b){
    return !(a < b);
}
bool operator<=(constBigInt&a,constBigInt&b){
    return !(a > b);
}
 
BigInt &BigInt::operator=(const BigInt &a){
    digits = a.digits;
    return *this;
}
 
BigInt &BigInt::operator++(){
    inti, n = digits.size();
    for (i = 0; i< n && digits[i] == 9;i++)
        digits[i] = 0;
    if(i == n)
        digits.push_back(1);
    else
        digits[i]++;
    return *this;
}
BigInt BigInt::operator++(int temp){
    BigInt aux;
    aux = *this;
    ++(*this);
    returnaux;
}
 
BigInt &BigInt::operator--(){
    if(digits[0] == 0 &&digits.size() == 1)
        throw("UNDERFLOW");
    inti, n = digits.size();
    for (i = 0; digits[i] == 0 &&i<n;i++)
        digits[i] = 9;
    digits[i]--;
    if(n > 1 && digits[n - 1] == 0)
        digits.pop_back();
    return *this;
}
BigInt BigInt::operator--(int temp){
    BigInt aux;
    aux = *this;
    --(*this);
    returnaux;
}
 
BigInt &operator+=(BigInt &a,const BigInt& b){
    int t = 0, s, i;
    int n = Length(a), m = Length(b);
    if(m > n)
        a.digits.append(m - n, 0);
    n = Length(a);
    for (i = 0; i<n;i++){
        if(i< m)
            s = (a.digits[i] + b.digits[i]) + t;
        else
            s = a.digits[i] + t;
        t = s / 10;
        a.digits[i] = (s % 10);
    }
    if(t)
        a.digits.push_back(t);
    returna;
}
BigInt operator+(const BigInt &a, const BigInt &b){
    BigInt temp;
    temp = a;
    temp += b;
    returntemp;
}
 
BigInt &operator-=(BigInt&a,const BigInt &b){
    if(a < b)
        throw("UNDERFLOW");
    int n = Length(a), m = Length(b);
    inti, t = 0, s;
    for (i = 0; i<n;i++){
        if(i< m)
            s = a.digits[i] - b.digits[i]+ t;
        else
            s = a.digits[i]+ t;
        if(s < 0)
            s += 10,
            t = -1;
        else
            t = 0;
        a.digits[i] = s;
    }
    while(n > 1 &&a.digits[n - 1] == 0)
        a.digits.pop_back(),
        n--;
    returna;
}
BigInt operator-(const BigInt&a,constBigInt&b){
    BigInt temp;
    temp = a;
    temp -= b;
    returntemp;
}
 
BigInt &operator*=(BigInt &a, const BigInt &b)
{
    if(Null(a) || Null(b)){
        a = BigInt();
        returna;
    }
    int n = a.digits.size(), m = b.digits.size();
    vector<int>v(n + m, 0);
    for (inti = 0; i<n;i++)
        for (int j = 0; j <m;j++){
            v[i + j] += (a.digits[i] ) * (b.digits[j]);
        }
    n += m;
    a.digits.resize(v.size());
    for (int s, i = 0, t = 0; i< n; i++)
    {
        s = t + v[i];
        v[i] = s % 10;
        t = s / 10;
        a.digits[i] = v[i] ;
    }
    for (inti = n - 1; i>= 1 && !v[i];i--)
            a.digits.pop_back();
    returna;
}
BigInt operator*(constBigInt&a,constBigInt&b){
    BigInt temp;
    temp = a;
    temp *= b;
    returntemp;
}
 
BigInt &operator/=(BigInt&a,const BigInt &b){
    if(Null(b))
        throw("Arithmetic Error: Division By 0");
    if(a < b){
        a = BigInt();
        returna;
    }
    if(a == b){
        a = BigInt(1);
        returna;
    }
    inti, lgcat = 0, cc;
    int n = Length(a), m = Length(b);
    vector<int>cat(n, 0);
    BigInt t;
    for (i = n - 1; t * 10 + a.digits[i]  <b;i--){
        t *= 10;
        t += a.digits[i] ;
    }
    for (; i>= 0; i--){
        t = t * 10 + a.digits[i];
        for (cc = 9; cc * b >t;cc--);
        t -= cc * b;
        cat[lgcat++] = cc;
    }
    a.digits.resize(cat.size());
    for (i = 0; i<lgcat;i++)
        a.digits[i] = cat[lgcat - i - 1];
    a.digits.resize(lgcat);
    returna;
}
BigInt operator/(const BigInt &a,const BigInt &b){
    BigInt temp;
    temp = a;
    temp /= b;
    returntemp;
}
 
BigInt &operator%=(BigInt&a,const BigInt &b){
    if(Null(b))
        throw("Arithmetic Error: Division By 0");
    if(a < b){
        a = BigInt();
        returna;
    }
    if(a == b){
        a = BigInt(1);
        returna;
    }
    inti, lgcat = 0, cc;
    int n = Length(a), m = Length(b);
    vector<int>cat(n, 0);
    BigInt t;
    for (i = n - 1; t * 10 + a.digits[i] <b;i--){
        t *= 10;
        t += a.digits[i];
    }
    for (; i>= 0; i--){
        t = t * 10 + a.digits[i];
        for (cc = 9; cc * b >t;cc--);
        t -= cc * b;
        cat[lgcat++] = cc;
    }
    a = t;
    returna;
}
BigInt operator%(const BigInt &a,BigInt&b){
    BigInt temp;
    temp = a;
    temp %= b;
    returntemp;
}
 
BigInt &operator^=(BigInt &a,const BigInt & b){
    BigInt Exponent, Base(a);
    Exponent = b;
    a = 1;
    while(!Null(Exponent)){
        if(Exponent[0] & 1)
            a *= Base;
        Base *= Base;
        divide_by_2(Exponent);
    }
    returna;
}
BigInt operator^(BigInt &a,BigInt& b){
    BigInt temp(a);
    temp ^= b;
    returntemp;
}
 
void divide_by_2(BigInt &a){
    int add = 0;
    for (inti = a.digits.size() - 1; i>= 0;i--){
        int digit = (a.digits[i] >> 1) + add;
        add = ((a.digits[i] & 1) * 5);
        a.digits[i] = digit;
    }
    while(a.digits.size() > 1 && !a.digits.back())
        a.digits.pop_back();
}
 
BigInt sqrt(BigInt & a){
    BigInt left(1), right(a), v(1), mid, prod;
    divide_by_2(right);
    while(left <= right){
        mid += left;
        mid += right;
        divide_by_2(mid);
        prod = (mid * mid);
        if(prod <= a){
            v = mid;
            ++mid;
            left = mid;
        }
        else{
            --mid;
            right = mid;
        }
        mid = BigInt();
    }
    returnv;
}
 
BigInt NthCatalan(int n){
    BigInt a(1),b;
    for (inti = 2; i<= n;i++)
        a *= i;
    b = a;
    for (inti = n + 1; i<= 2 * n;i++)
        b *= i;
    a *= a;
    a *= (n + 1);
    b /= a;
    returnb;
}
 
BigInt NthFibonacci(int n){
    BigInt a(1), b(1), c;
    if(!n)
        returnc;
    n--;
    while(n--){
        c = a + b;
        b = a;
        a = c;
    }
    returnb;
}
 
BigInt Factorial(int n){
    BigInt f(1);
    for (inti = 2; i<= n;i++)
        f *= i;
    returnf;
}
 
istream&operator>>(istream&in,BigInt&a){
    string s;
    in >>s;
    int n = s.size();
    for (inti = n - 1; i>= 0;i--){
        if(!isdigit(s[i]))
            throw("INVALID NUMBER");
        a.digits[n - i - 1] = s[i];
    }
    returnin;
}
 
ostream&operator<<(ostream&out,const BigInt &a){
    for (inti = a.digits.size() - 1; i>= 0;i--)
        cout<< (short)a.digits[i];
    returncout;
}
 
intmain()
{
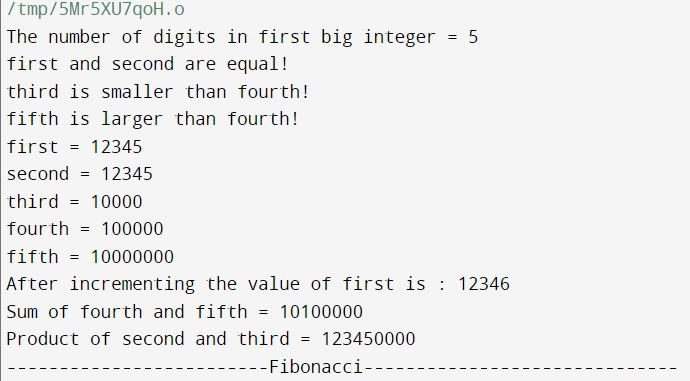
    BigInt first("12345");
    cout<< "The number of digits"
         << " in first big integer = "
         << Length(first) << '\n';
    BigInt second(12345);
    if (first == second) {
        cout<< "first and second are equal!\n";
    }
    else
        cout<< "Not equal!\n";
    BigInt third("10000");
    BigInt fourth("100000");
    if (third < fourth) {
        cout<< "third is smaller than fourth!\n";
    }
    BigInt fifth("10000000");
    if (fifth > fourth) {
        cout<< "fifth is larger than fourth!\n";
    }
 
    cout<< "first = " << first << '\n';
    cout<< "second = " << second << '\n';
    cout<< "third = " << third << '\n';
    cout<< "fourth = " << fourth<< '\n';
    cout<< "fifth = " << fifth<< '\n';
 
    first++;
    cout<< "After incrementing the"
         << " value of first is : ";
    cout<< first << '\n';
    BigInt sum;
    sum = (fourth + fifth);
    cout<< "Sum of fourth and fifth = "
         << sum << '\n';
    BigInt product;
    product = second * third;
    cout<< "Product of second and third = "
         << product << '\n';
 
    
    cout<< "-------------------------Fibonacci"
         << "------------------------------\n";
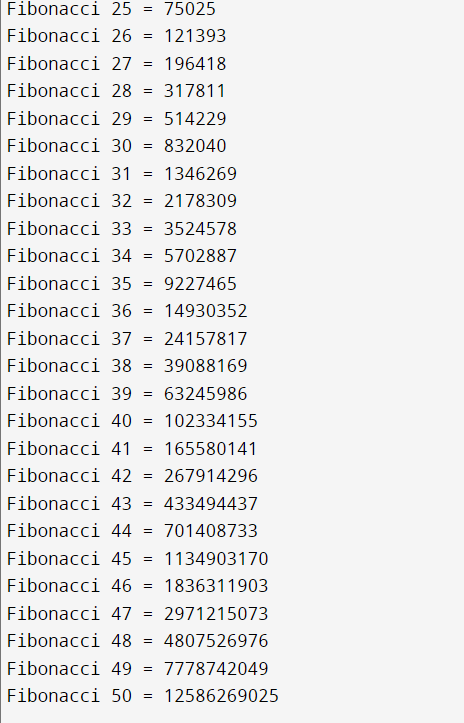
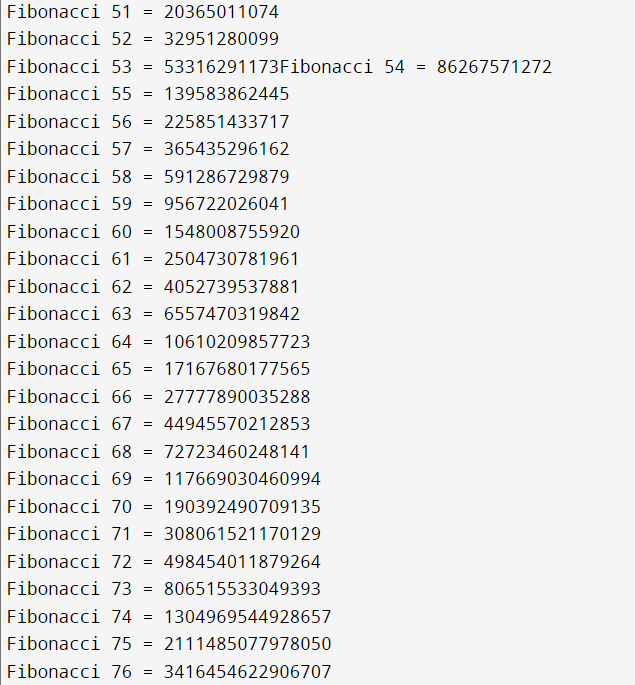
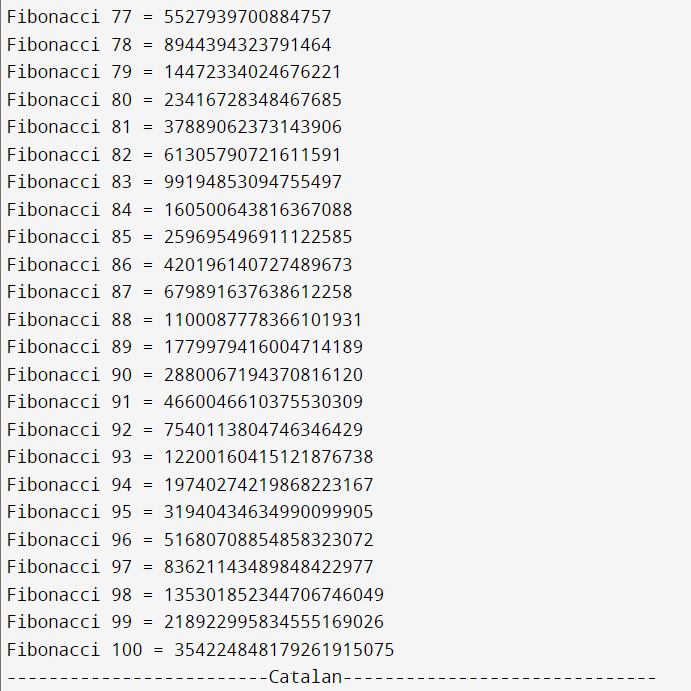
    for (inti = 0; i<= 100; i++) {
        BigInt Fib;
        Fib = NthFibonacci(i);
        cout<< "Fibonacci " <<i<< " = " << Fib<<'\n';
    }
    cout<< "-------------------------Catalan"
         << "------------------------------\n";
    for (inti = 0; i<= 100; i++) {
        BigInt Cat;
        Cat = NthCatalan(i);
        cout<< "Catalan " <<i<< " = " << Cat<<'\n';
    }


    cout<< "-------------------------Factorial"
         << "------------------------------\n";
    for (inti = 0; i<= 100; i++) {
        BigInt fact;
        fact = Factorial(i);
        cout<< "Factorial of "
             <<i<< " = ";
        cout<< fact << '\n';
    }
}

Output:

Bigint (BIG INTEGERS) in C with Example Bigint (BIG INTEGERS) in C with Example Bigint (BIG INTEGERS) in C with Example Bigint (BIG INTEGERS) in C with Example Bigint (BIG INTEGERS) in C with Example Bigint (BIG INTEGERS) in C with Example

Related Topics

If else Programs in C Programming

If else Programs in C programming The if-else statement in C is based on some particular conditions to perform the operations. If and only if the given condition is valid, the operations listed in...

4 minutes read.

Entry Control Loop in C

Initially, an entry control loop verifies the termination condition at the entry point. After that, its control passes to the main body of the while or for loop if the...

3 minutes read.

Formatted Input and output function in C

Formatted I/O functions display multiple outputs to the user by taking various inputs. All data types like int, float, char and double are supported by the formatted I/O function. In...

4 minutes read.

Data Structures And Algorithms in C

C language is one of the most flexible and simple languages. So, it is always better to learn any concept in C language compared to other languages. Let us look...

13 minutes read.

Factorial Program in C using For Loop

Before move on the factorial program. We have to know about the for loop in C programming language. The syntax of the For Loop is: for (initialization statement; test expression; an increment...

3 minutes read.

C Program of Fencing the Ground

The college's ground is rectangular. Fencing the ground the management makes the decision to construct a fence around the ground. They planned to wrap a thick rope around the ground...

1 minute read.

Snake Game in C

Snake game in C is basic desktop console program which was created in 1970’s. It is an old classic game which was played by every child across the world. This...

4 minutes read.

Palindrome Number in C

What is a Palindrome? A number that doesn't change when reversed is known as a palindrome. We reverse a number and compare it to the original number to determine whether it is...

4 minutes read.

How to find square root in C Language

Before understanding the square root program in C language, one must know about the square root of a number. A square root is a mathematical term. The square root of a...

5 minutes read.

Infix to Postfix program in C

Infix Expression: In infix expression, an operator is placed between the two operands. Example: x + y, here operator + is placed between operands x and y. Postfix Expression: In...

3 minutes read.

Long int in C

We use data type to avoid the type of data to be stored for a variable at the time of declaration.So, we can say that the variable type is known...

3 minutes read.

Add two numbers using the function in C

Here we will learn how to add two numbers by creating function in C. Let’s learn this with help of example. Code: - #include <stdio.h> int add_two_no(int a, int b); int main(){   int first_num,...

1 minute read.

Decimal to Binary in C

What is a decimal number? A decimal number is a number represented in the decimal number system. This system of binary conversion uses base 10 to represent numbers, i.e. the digits...

3 minutes read.

Write a program that produces different results in C and C++

In this tutorial, we'll explore several programs that, depending on whether they are developed using C or C++ compilers, will produce varying outputs. There are numerous similar programs, but we will just...

2 minutes read.

2f in C language

Float data type in c: Double-precision floating-point numbers with up to 17 significant digits are stored in the FLOAT data type. FLOAT is equivalent to C's double data type and IEEE...

3 minutes read.

C program to find factorial of a number using Recursion

What does the term "Factorial of a Number" mean? In mathematics, factorial is the product of all positive integers that are less than or equal to a certain positive integer, and...

2 minutes read.

Do-While Loop in C

Both 'While' and 'Do-While' loops in C mostly have a similar concept, and the code of both loops runs for mainly similar purposes in the same manner. But, there is...

3 minutes read.

Flow Chart of For loop in C

This is a flowchart that represents the process of executing the for loop in the C programming language. Generally, as we know there are three main components of for loop:1. The...

3 minutes read.

How to create a binary file in C?

Creating a binary file in C language is very simple, requiring only some specific functions to be implemented. There are also other binary modes: read, and write, which will be...

7 minutes read.

What is a buffer in C?

A buffer is an area of memory set aside for the temporary storage of data. A data buffer (or just buffer) is a region of a physical memory storage used to...

5 minutes read.