Tree in C
Introduction:
"A tree describes a type of hierarchical structure of data in which sides join units together. The way it works is recursive, which indicates that it is composed of numerous miniature versions of oneself." Information is saved using trees because they make it simple for people to browse through them.
In C, pointers and structures may be employed to create trees. The root node can have zero, one, or two offspring of the nodes, with a permitted number of 2.
The root and child nodes are the terms used to describe the highest as well as lowermost elements of a tree, respectively. Every node can contain a number of children, plus these offspring may spawn children of their own, thus creating a recursive structure.
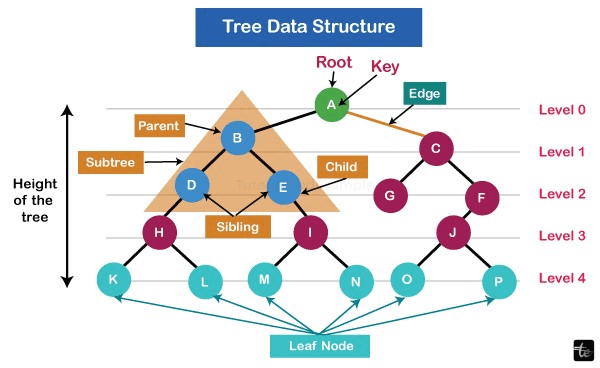
Simple Tree Data Structure Terminologies:
- Parent Node: A node's parental node is the node that came before it in the tree of nodes. The most recent node of "D, E" is "B."
- Children Node: The node, which is a node's direct descendant, is referred to as a tree's children node. Such as, The youngest nodes of B are "D" and "E."
- Root Node: The highest node in the structure of a tree or node in general that has no parents is referred to as a root node. The tree's root point is designated as A. Non-empty trees must have a single base node along with the path connecting it to each of the other nodes.
- Leaf Nodes or External Nodes: Leaf nodes represent nodes that don't have any child nodes. The nodes that make up the leaves of the tree are K, L, M, N, O, and P.
- Node's ancestors: All previous nodes on the route from the starting point to that component are referred to as that node's ancestors. The ancestor connections of the node "E" are "A" and "B."
- Node Descendant: Every succeeding node along the line connecting the leaf node with the previous node is a descendant. The children of the node "B" are "E" and "I."
- Siblings: Siblings are kids of the same parent node. The terms "D " and, E" are siblings.
- Node's level: The number of connections on the route between the base node and a node indicates that node's level. The level of the root node is 0.
- Any node having a minimum of a single kid is referred to as a node within itself.
- Neighbor of a Node: This node's predecessors or offspring are referred to as its next-door neighbors.
- Every node of the tree's subtree, including its offspring.
Example of the Tree Data Structure:
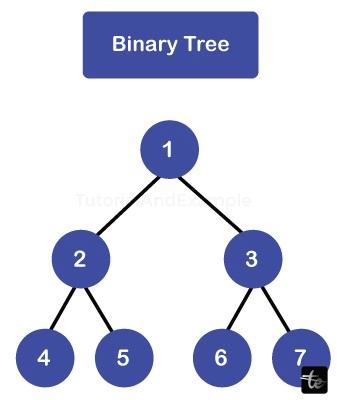
Here,
- The root node is Node 1.
- The parent of 2 and 3 is 1.
- Two and three are cousins.
- The leaf nodes are 4, 5, 6, and 7.
- 5 has the ancestors 1 and 2.
Different kinds of trees:
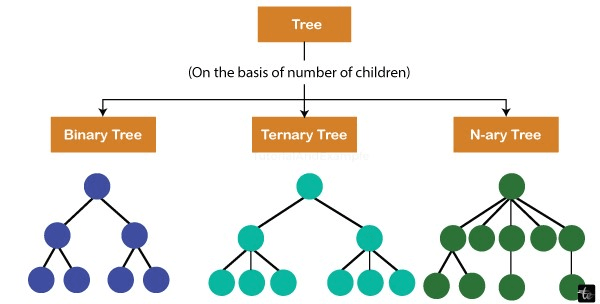
1. Binary Tree: A binary tree allows for no more than two offspring to be connected to a single node. Complete binary trees, comprehensive binary trees, and balanced binary trees, including unstable or deformed binary trees, are a few examples of frequent binary forest types.
2. Ternary Tree: The ternary tree is a type of tree data structure where every node has a maximum of three offspring, which are typically labeled "left," "mid," and "right."
3. N-ary Tree: Generic trees, also known as N-ary trees, are collections of nodes, every one of which is a data structure made up of entries plus a list of connections to the node's offspring. Every node maintains the addresses of numerous other nodes, excluding the linked list.
Basic Operation Of Tree Data Structure:
- Create: In the data structure, build a tree.
- Insert: Insert Adds data to a tree.
- Search: To determine if a piece of certain data exists or not, use the lookup function.
- Traversal:
Preorder traversing is the act of moving through a data structure's trees in a preordered fashion.
Conduct an in-order traversal by moving through a tree.
Conduct post-order traversal, which involves moving through a tree.
Advantages:
- Tree data structures have the benefit of rapid searching. Considering median search durations for O(log n) with symmetrical trees like AVL, according to what kind of tree.
- Massive amounts of information may be easily organized as well as navigated because of trees' tiered arrangement of data.
- Trees are simple to navigate along and modify utilizing recurrent methods because of their recursive structure.
Disadvantages:
- Unbalanced trees, or trees where the height is lopsidedly distributed on a single side, might prolong research times.
- Particularly if the structure itself is quite big, trees take greater amounts of memory over other data structures, such as arrays along with linked lists.
- It can be not easy to design and manipulate trees, although doing so requires a solid grasp of the underlying methods.
Uses of Tree Data Structure:
- File Format: This makes file organizing and searching easy.
- Data compressing: Huffman's coding method, a well-liked one, creates a binary tree of data with the leaves denoting words as well as their rate of occurrences. The data is encoded using the tree, which results in an approach that requires the smallest amount of storage.
- A code syntax tree is utilized in the design of compilers to depict the inner workings of a program.
- Databases index: To effectively find and access data, B-trees, as well as other tree topologies, are employed in data searching.