Error Correction and Error Detection

Error Correction and Error Detection

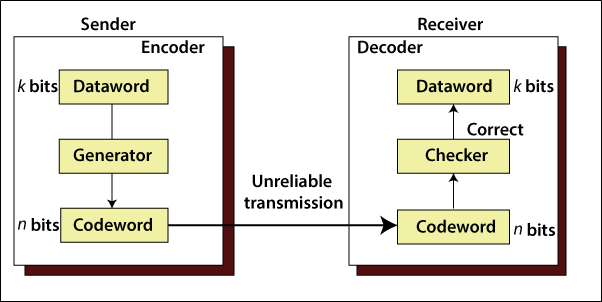
Error correction and error detection techniques are work on the data-link layer. The data link layer ensures the frames are sent from the sender to the receiver with accuracy. Error correction is more difficult than error detection.

Error

An error is a situation when the data send by the sender and receive by the receiver, but that data doesn't match the sender data.

For example, the sender sends the 0101010 data, and the receiver receives the 1101010.

Types of Error

1. Single bit error
2. Burst error

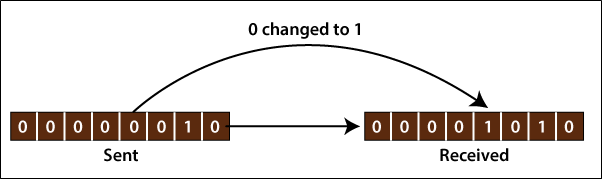
Single-bit error: In the single-bit error, only one bit is changed in the frame. For example, the sender sends the data (01010100) in the frame, and the receiver receives the data (11010100) in the frame.

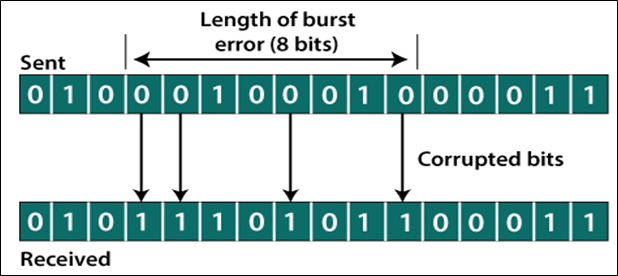
Burst error: In the burst error, one or more than one bits is changed in the frame. For example, the sender sends the data (01010100) in the frame, and the receiver receives the data (11010100) in the frame.

Redundancy

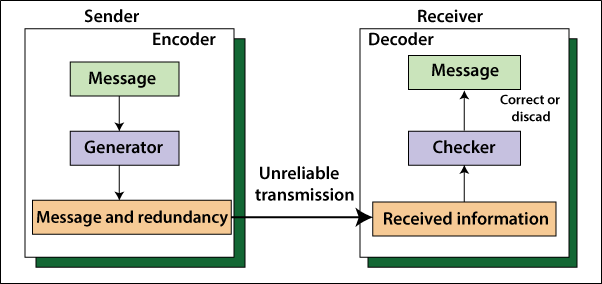
The main concept of error detection and error correction is redundancy. To the error detection and error correction, redundancy adds some extra redundant bits in the bits. The sender adds these redundant bits, and the receiver eliminates these redundant bits.

Coding

Redundancy is achieved by way of various coding schemes. The sender introduces redundant bits by establishing a connection between the redundant bits and the actual data bits. The receiver checks the relationship between the redundant bits and the actual data bits to detect the error. Coding schemes can be divided into two categories: block coding and convolution coding. Block coding is less complex than the convolution coding.

 

Error Detection

Error detection is the method of identifying errors. To identify these errors, it uses some redundancy codes. Redundancy codes added in actual data, and it has transmitted by the sender. These codes are known as error detection codes.

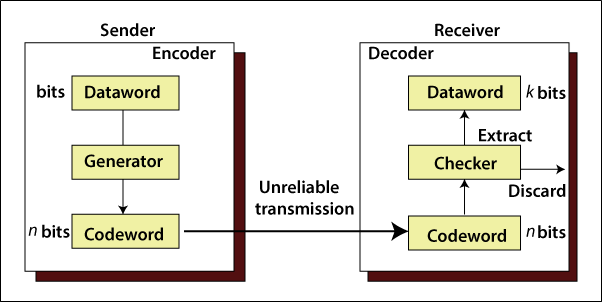
Types of error detection techniques:

1. Parity Checking
2. Cyclic Redundancy Check (CRC)
3. Checksum

Parity Checking

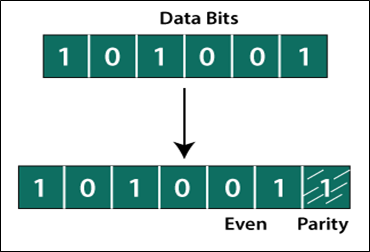
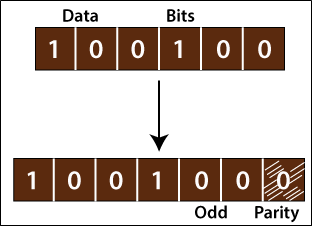
Parity Checking is also known as the Vertical redundancy check (VRC). Parity checking is a very simple technique. There are two cases in the parity checking techniques:

Even parity: If the number of 1's is even in the frame, 0 is added in the frame. The even-parity example shown in the figure below.

Odd parity: If the number of 1's is odd in the frame, 1 is added in the frame. The odd-parity example shown in the figure below.

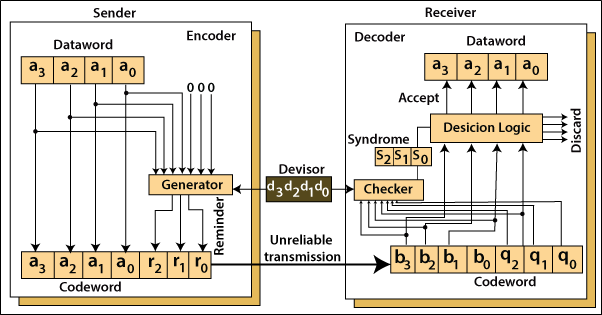
Cyclic Redundancy Check

The cyclic redundancy check was developed by W-Wesley Peterson in 1961. It is a technique that is used to find errors in digital-data. The cyclic redundancy check is very easy to implement in hardware. It can be analyzed mathematically. The cyclic redundancy check is more effective than VRC and LRC techniques in detecting errors. VRC and LRC are based at the binary-addition, whereas the CRC is based at the binary-division.

The important points of CRC are following in the below.

• If the remainder is non-zero arrives after doing the Binary Division, that data is not error-free.
• If the remainder zero arrives after doing binary division, that data is error-free.

For better understand, let take an example.

Example 1                                  Data word = 110101

                                                   Divisor = 1010

Step 1: We can see that the divisor is of 4 bits, so we have to add (4-1) 0 to the data word.

                                                   Data word = 110101000

1010) 110101000 (111011                                            1010                                              1110                                              1010                                                1001                                                1010                                                  0110                                                  0000                                                    1100                                                    1010                                                      1100                                                      1010                                                        110

The remainder is non-zero, so that will be again the binary division.  

1010) 110101110 (111011                                                         1010                                                           1110                                                           1010                                                             1001                                                             1010                                                                 0111                                                                 0000                                                                   1111                                                                   1010                                                                     1010                                                                      1010                                                                     0000

Now, the remainder is all zero. Hence, the data has error-free.

Checksum

The checksum is an error detection technique. It can be applied to any information. The checksum is mostly used at the network layer and transport layer rather than the data-link layer. 

At the sender side, each m bit of the data is divided into k segments. The segments are added with the 1's complement arithmetic at the sender end to get the sum. At the end of the receiver, all segments obtained are added using the arithmetic 1's complement to get the sum.

• If the value is 0, the obtained data is accepted.
• If the value is non-zero, the obtained data is discarded.

For better understand, let take an example, Suppose the sender wants to transmit 4-frames each of 8-bits. The frames are 11010100, 10101001, 00101100, and 01011100.

At the sender side, add first two frames    

11010100 10101001                                           101111101     Now, 1 is the shift                                             01111101                                                           1                                             01111110 Now, add the third frame of this addition of first two frames                                             01111110                                             00101100                                             10101010 Now, add the fourth frame                                             10101010                                             01011100                                           100000110 Now, 1 is the shift                                                           00000110                                                          1                  Sum =               00000111  Checksum is 1’s complement of sum =      11111000

At the receiver side, add first two frames          

11010100 10101001                                           101111101     Now, 1 is the shift                                             01111101                                                           1                                             01111110 Now, add the third frame of this addition of first two frames                                             01111110                                             00101100                                             10101010 Now, add the fourth frame                                             10101010                                             01011100                                           100000110 Now, 1 is the shift                                                           00000110                                                          1                                            00000111 Now, add checksum                                            00000111                                            11111000                                            11111111 Complement:                     00000000  The complement value is zero.  Hence, all frames have been accepted.

Error Correction

Error correction is more difficult than error detection. Error correction codes are used to detect and correct errors when transmitting data from the sender to the receiver. It can be done in two ways:

1. Backward Error Correction
2. Forward Error Correction

Backward Error Correction: If the receiver receives an error in the received data, it tells the sender to retransmit the data again.

Forward Error Correction: If the receiver finds an error in the received data, the error correction codes correct these errors automatically.