How to Merge Array in C?

Introduction

Merging arrays is a common task for many developers but might be difficult for beginners of C programming. Fortunately, our guide will show you how to quickly merge arrays in C with just a few lines of code. This article will cover the basics of merging arrays in C and provide some tips and tricks for advanced users. Once you've finished reading, you'll clearly understand how to combine two or more arrays in C Language.

What is an Array?

Arrays store the values or variables of the same datatype. Like a spreadsheet row or column, an array consists of linear elements.

Typically, Arrays are represented in programming languages as contiguous blocks of memory. Array’s elements are accessed using their indexes. The array element’s index represents their position.

With arrays, you can access and modify elements quickly and easily, allowing you to store and manipulate large amounts of data. Also helpful in storing logically ordered data, such as a list of names or a sequence of numbers.

The element of an array is typically defined by specifying the type, the number of factors, and the type of element. For example, C array of ten integers can be defined as follows:

int my_array[10];

It can hold up to 10 integers, and its elements are accessed by indices 0 to 9. You would use index 0 to access the Array's first element.

int fisrt_element = my_array[0];

A wide range of applications uses arrays in computer science. They are often used with loops to solve complex problems.

What is a Merging of Array?

Merging arrays is the process of combining two or more arrays into a single display. Developers frequently used this technique when working with large data sets. Merging two arrays requires careful consideration of the order in which the elements combine the two arrays.

How can we Merge Array in C?

Arrays are essential coding and programming components, making it possible to store multiple values and manipulate them as single entities. As such, it is crucial to know how to combine two arrays. Merging of arrays is an ordinary operation that is often necessary for problem-solving.

Here is an algorithm for merging two arrays in C with runtime input:

• Declare three arrays: A, B, and C. A and B will be the arrays we want to merge, and C will be the resulting combined Array.
• Prompt the user to input the size of A and B. Store these values in variables sizeA and sizeB, respectively.

• Prompt the user to input the elements of A and B. Insert these Elements in another array.

• Initialize variables i and j to 0. These will be used as indices to keep track of the current position in A and B, respectively.

• Initialize a variable k to 0. it will be used as an index to keep track of the current position in C.

• While i is less than sizeA and j is less than sizeB, do the following: a. Compare the elements in index i and j in A and B, respectively.  b. component of A is less than element B, add the element from A to C and increment I by 1. c. a part in B is less than that of A, add an element from B to C and increment j by 1.

• After compiling the loop in the above statement, one of the arrays, A or B, will be fully processed, and the other will still have some remaining elements. We need to add the remaining elements from the non-empty Array to C.

Overall, this algorithm is a simple and efficient way to merge two sorted arrays in C. It can be helpful in various situations where it is necessary to combine two sorted

arrays, such as in sorting algorithms or when merging two sorted lists.

Here is an example of an algorithm for merging two arrays in C with runtime input:

#include <stdio.h>
int main() {
  int sizeA, sizeB,A[sizeA], B[sizeB], C[sizeA + sizeB];
  printf("Enter the size of array A: ");
  scanf("%d", &sizeA);
  printf("Enter the size of array B: ");
  scanf("%d", &sizeB);


  printf("Enter the elements of array A: ");
  for (int i = 0; i < sizeA; i++) {
  	printf("\nA[%d]",i);
    scanf("%d", &A[i]);
  }


  printf("Enter the elements of array B: ");
  for (int i = 0; i < sizeB; i++) {
  	printf("\nB[%d]",i);
    scanf("%d", &B[i]);
  }


  int i = 0, j = 0, k = 0;
  while (i < sizeA && j < sizeB) {
    if (A[i] < B[j]) {
      C[k] = A[i];
      i++;
    } else {
      C[k] = B[j];
      j++;
    }
    k++;
  }


  while (i < sizeA) {
    C[k] = A[i];
    i++;
    k++;
  }


  while (j < sizeB) {
    C[k] = B[j];
    j++;
    k++;
  }


  printf("The merged array is: ");
  for (int i = 0; i < sizeA + sizeB; i++) {
    printf("%d ", C[i]);
  }
  printf("\n");


  return 0;
}

Explanation:

The above code first prompts the user to input the size of arrays A and B and then the elements of these arrays. It then initializes variables i, j, and k to 0. These will be used as indices to keep track of the current position in A, B, and C, respectively.

The algorithm then enters a loop that compares the elements in index i and j in A and B, respectively. The component of A is less than B; it adds the element from A to C and increments I by 1. the element in B is less than that in A; it adds the element from B to C and increments j by 1. This loop continues until one of the arrays, A or B, has been fully processed.

After the above loop is complete, one of the arrays, A or B, will be fully processed, and the other will still have some remaining elements. The algorithm then enters two separate loops to add the remaining components from the non-empty Array to C.

Finally, the code prints the merged array in C.

Output:

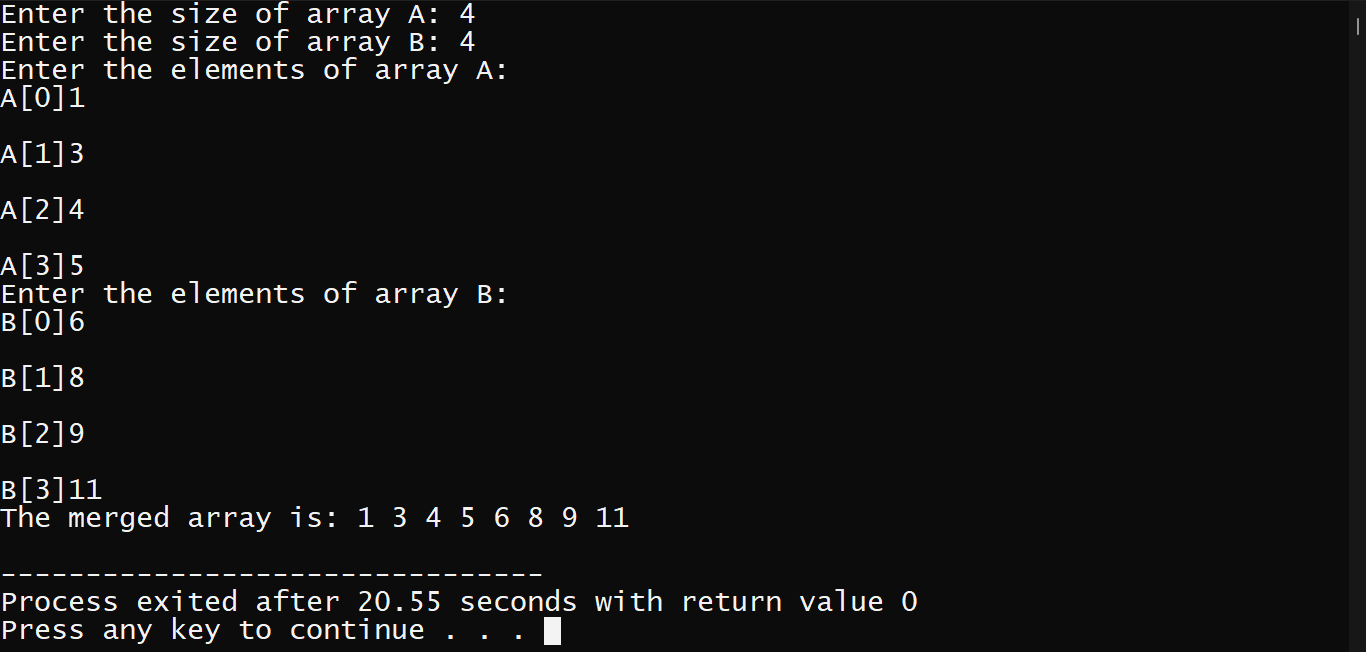
The complexity of Merging of Array

• Time Complexity:
  
  The algorithm's time complexity for merging two arrays in C is O(n), where n is the total number of elements in both arrays. It is because the algorithm uses a single pass through both arrays to merge them, and the number of features that are processed is proportional to the total number of elements in the two input arrays. In this case, the time complexity is linear in the input size, which means that the amount of time required by the algorithm grows linearly with the size of the information.

• Space Complexity:-
  
  The space complexity of the algorithm for merging two arrays in C is O(n), where n is the total number of elements in both collections. It is because the algorithm uses a single additional array, C, to hold the merged result, and the size of this Array is proportional to the total number of elements in the two input arrays. In this case, the time complexity is linear in the input size, which means that the amount of time required by the algorithm grows linearly with the size of the information.
  
  It's worth noting that there are other algorithms for merging two arrays that may have different space complexities and time complexities. For example, some algorithms may not require an additional array to hold the combined result, which could lead to lower space complexity. However, the specific space complexity of an algorithm will depend on the particular approach used.

Conclusion:-

Here are some additional points to consider in the conclusion of an algorithm for merging two sorted arrays in C:

• The algorithm is only applicable to sorted arrays. If the collections still need to be sorted, who must sort them before they can merged using this algorithm? It can be done using an efficient sorting algorithm, such as quicksort or merge sort
• The algorithm requires an additional array to store the merged result. This Array must be large enough to hold all elements from the two input arrays. If the combined size of the input arrays exceeds the available memory, the algorithm will not be able to complete it successfully.

• The algorithm has a linear time complexity so it will perform well even for large input arrays. It makes it a good choice for situations where the collections expect to be significant or where the algorithm will use frequently.

• The algorithm is relatively simple and easy to understand, which makes it a good choice for beginners learning how to merge two sorted arrays in C. However, it is also efficient enough for use in more advanced applications.

• The algorithm for merging two sorted arrays in C is valuable for combining two sorted lists or arrays into a single, sorted result. It is an efficient and straightforward way to perform this task and is well-suited for various applications.