2-3 Trees and Basic Operations on them
2-3 Trees, like any other AVL trees or B-trees, are just a type of Height Balanced Tree. 2-3 Trees are the B-trees of order 3. Like every other B-tree, the leaf nodes of such trees are always at the same depth; hence, the height needs to be consistently adjusted on each update, either insertion or deletion.
The time complexity of various operations like Search, Insert, or deletion is O(logN).
Properties of 2-3 trees
The nodes of a 2-3 tree are classified into three categories. One type of node, also called the 2-node, has only one value and two sub-nodes. At the same time, the 3-node(s) have two data items and three sub-nodes. The third type of node is the leaf node. The data items stored in a 2-3 tree are always sorted, and each node in such trees can only be of one type of these three. The insertions in 2-3 trees are done through the leaf nodes only, and the height is adjusted accordingly.
The primary operations performed on a 2-3 tree are as follows:
- Searching
- Insertion
- Deletion
Let us try to understand each of them one by one:
Searching
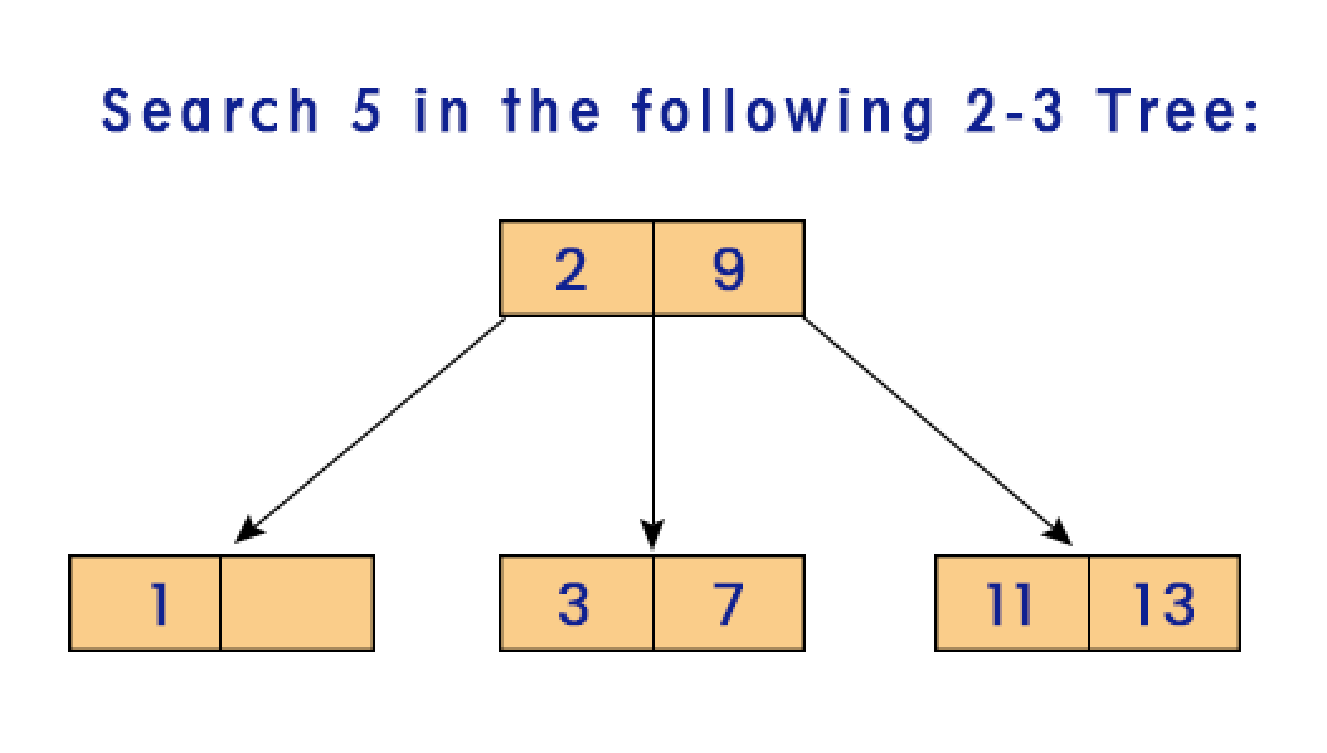
In order to find any specific target value from a 3-order B-tree, you can use this recursive algorithm that returns either TRUE if the value is present or FALSE if the data item specified is not present in the tree in O(logN) time. Let us represent our 2-3 tree as Tr and try to search a value, say target.
The base case for the algorithm would be:
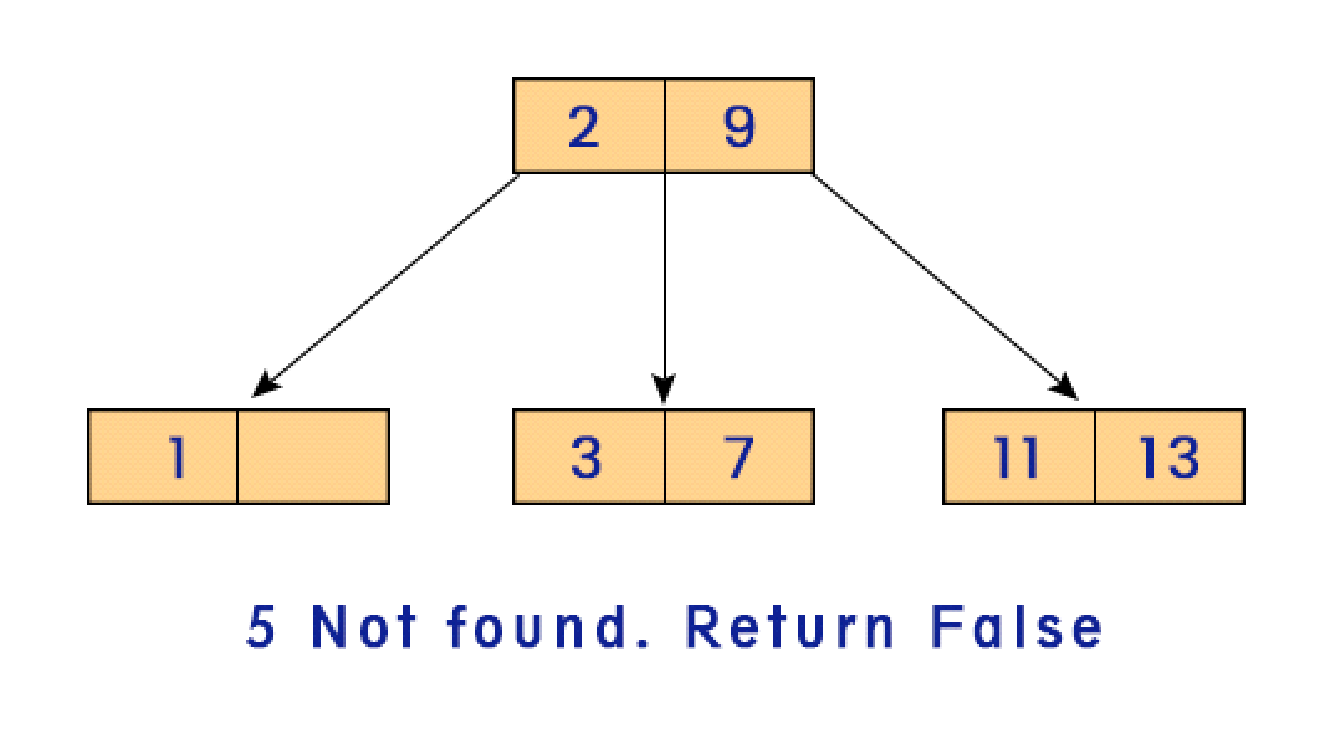
- If the tree is empty, Return FALSE (the empty tree cannot contain any value).
- If you reach the leaf node and still do not find the target, return FALSE.
- If you find the target at the current node, return TRUE.
Instructions that are called recursively:
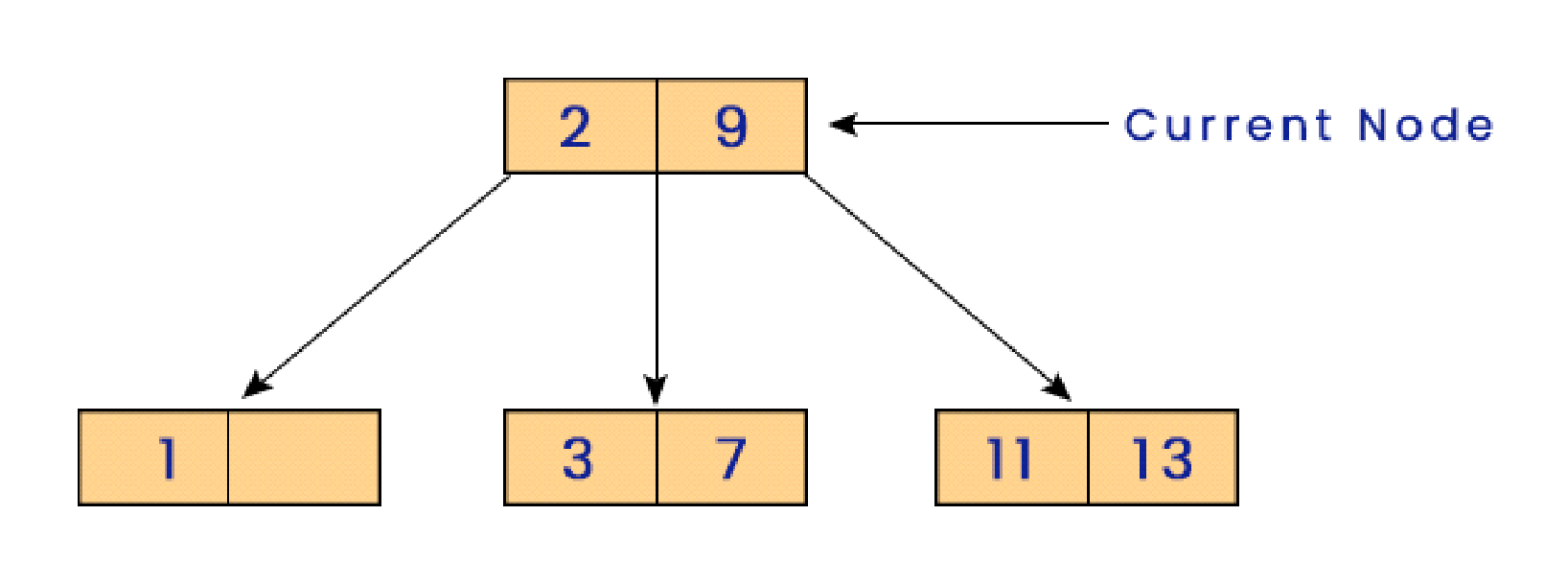
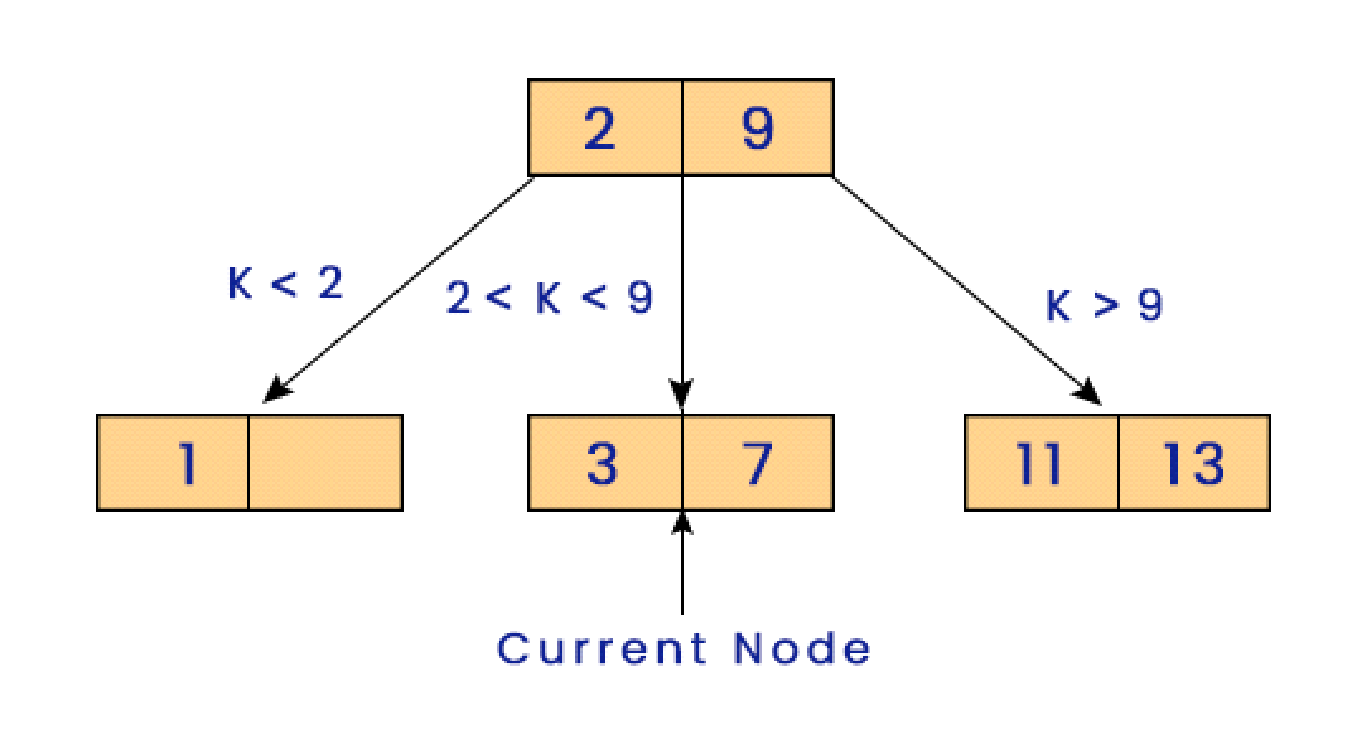
As we know that the Tr is already a sorted tree, we use the binary search approach.
1. In case that target>Node.leftInfo, recursively call search for the left subtree of the node you are currently checking.
2. And if the target>Node.rightInfo, we search the target in the right subtree of the node we checked.
3. Otherwise, if the target is larger than the node.leftInfo but smaller than the Node.rightInfo, then explore the middle subtree.
Insertion
While inserting your data in a 2-3 tree, you can find three possible cases. These cases are explained here briefly. As insertion is done only at the leaf nodes in a tree, the potential instances you are likely to encounter are:
Case 1: The leaf node has only one data item. The insertion is pretty simple in this case, as you can directly insert the value at that node itself.
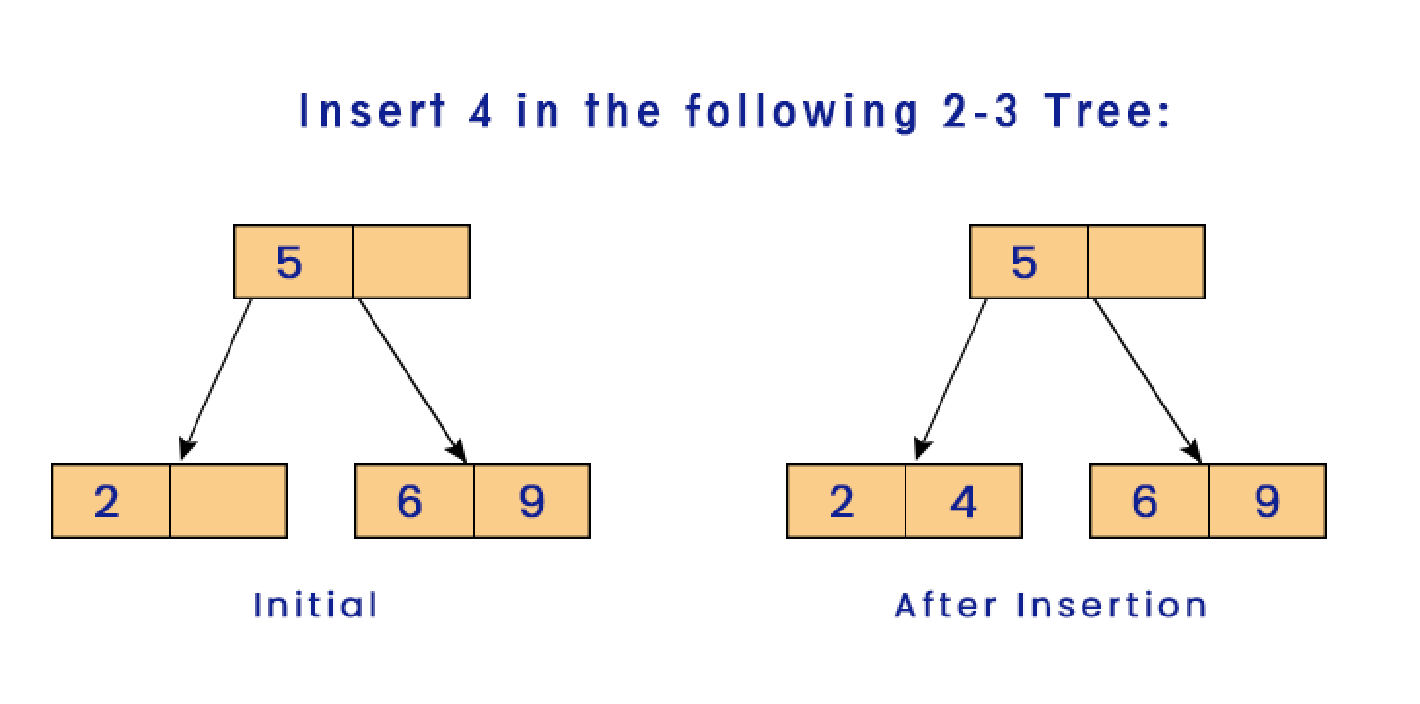
Case 2: Leaf nodes have two data items, but the parent contains only one data item. In such a case, the leaf node is temporarily converted into a 3-item node with three data items. Then the middle element is moved to the parent node to split the current node, eliminating any three-item nodes from the tree.
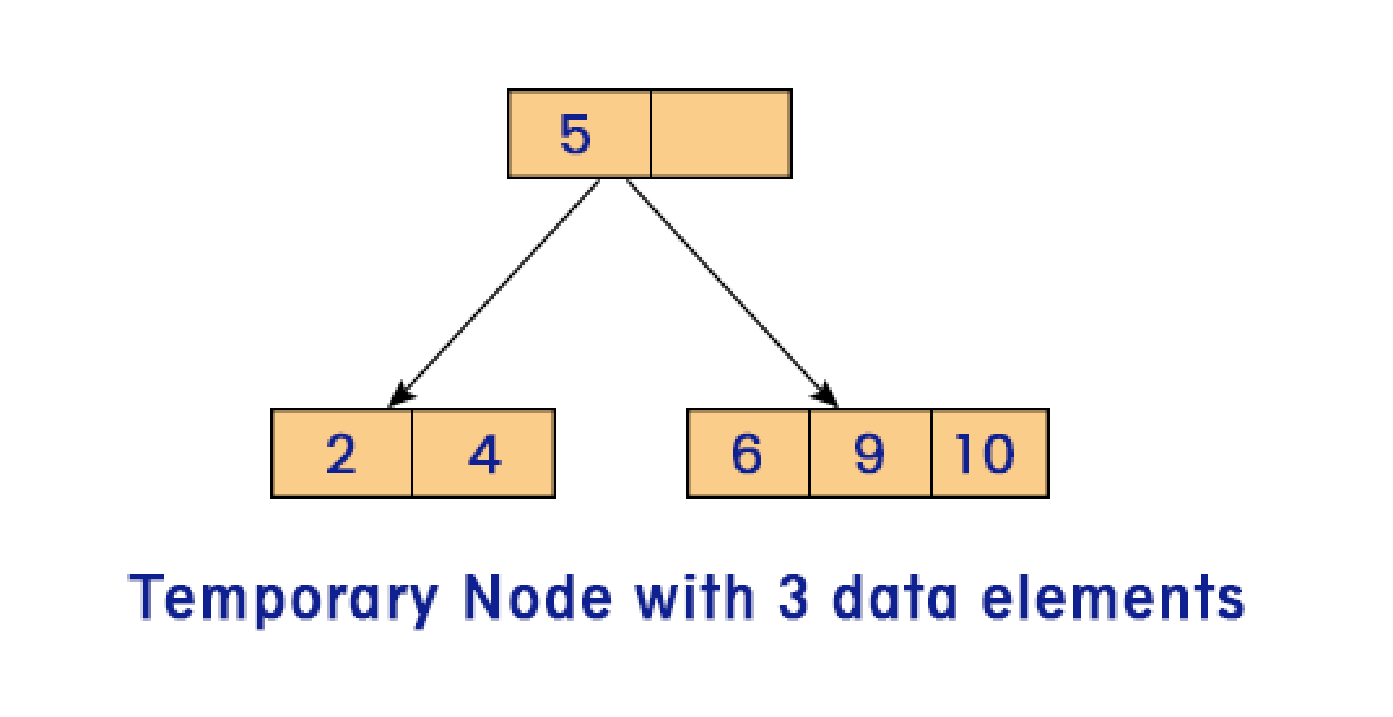
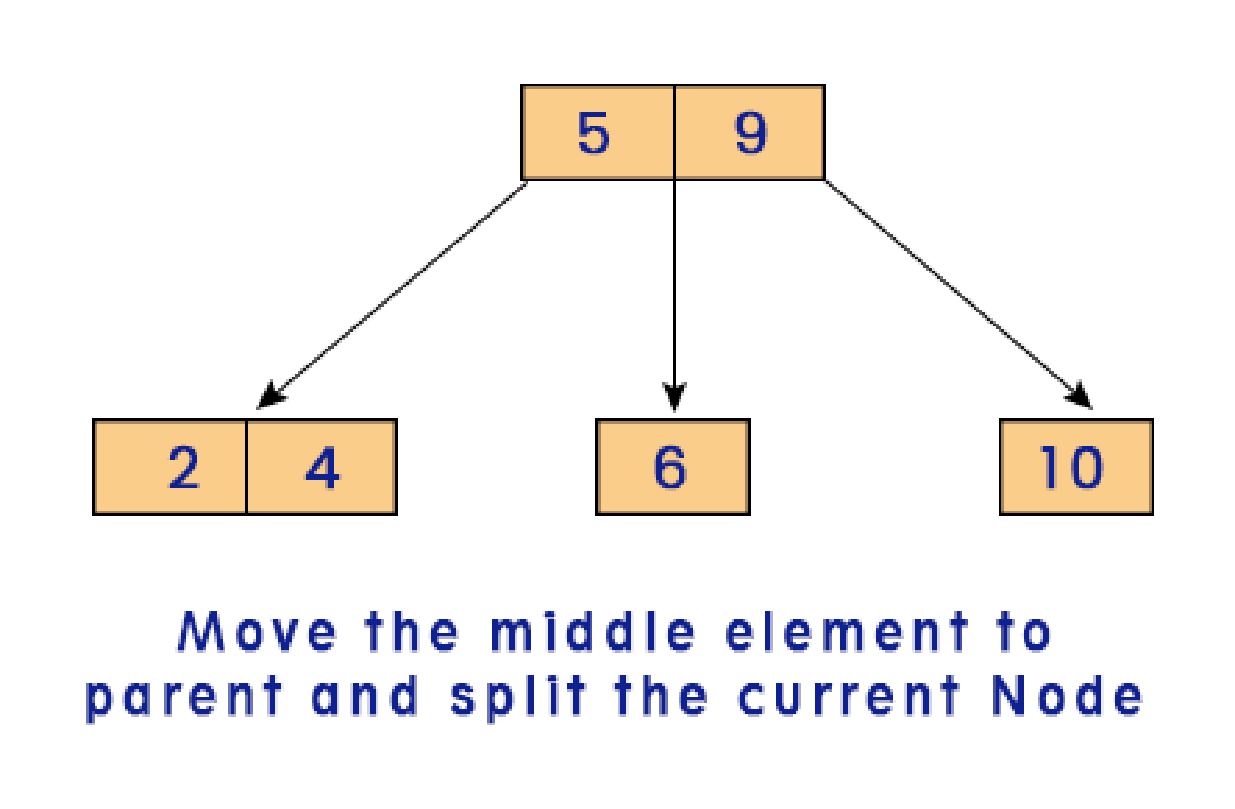
Case 3: Leaf nodes have two data elements as well as their parent node. In such cases, the process of case 2 is repeated until no 3 item nodes are left in the hierarchy, hence automatically adjusting the height of your tree.
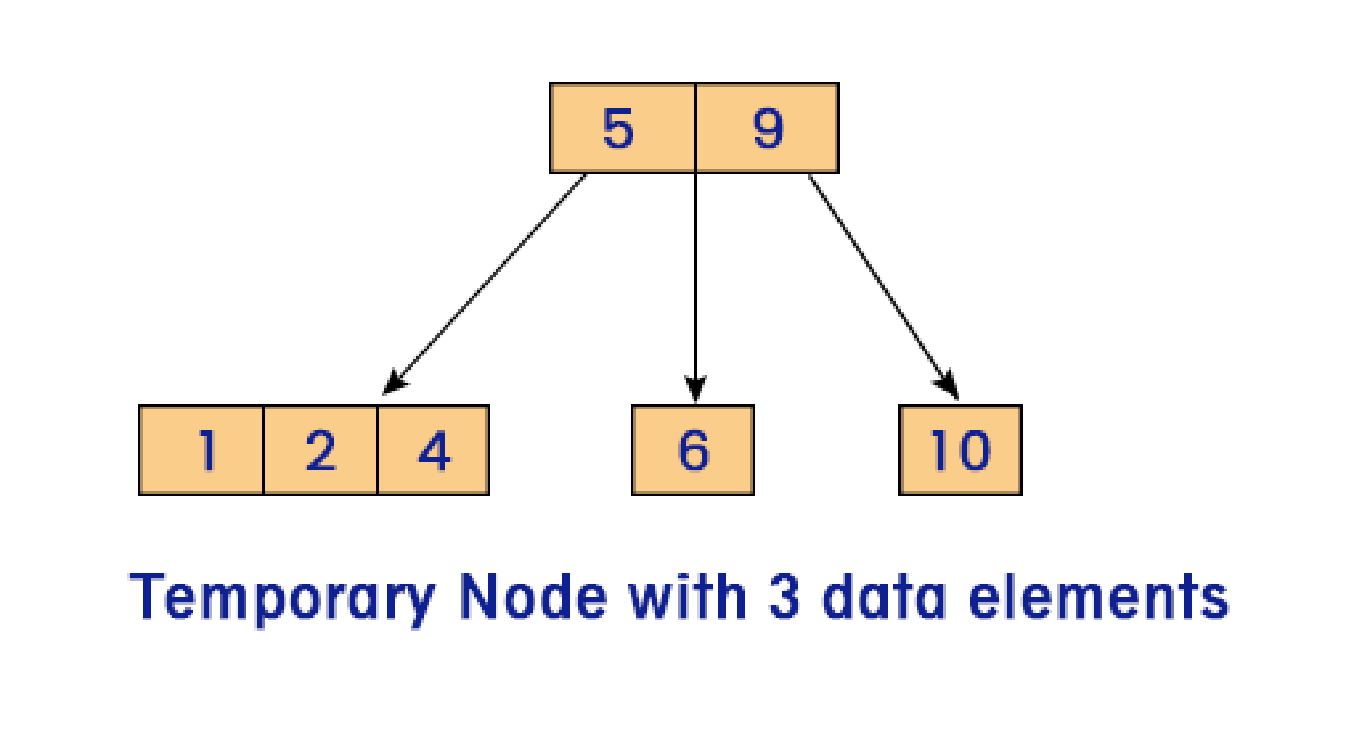
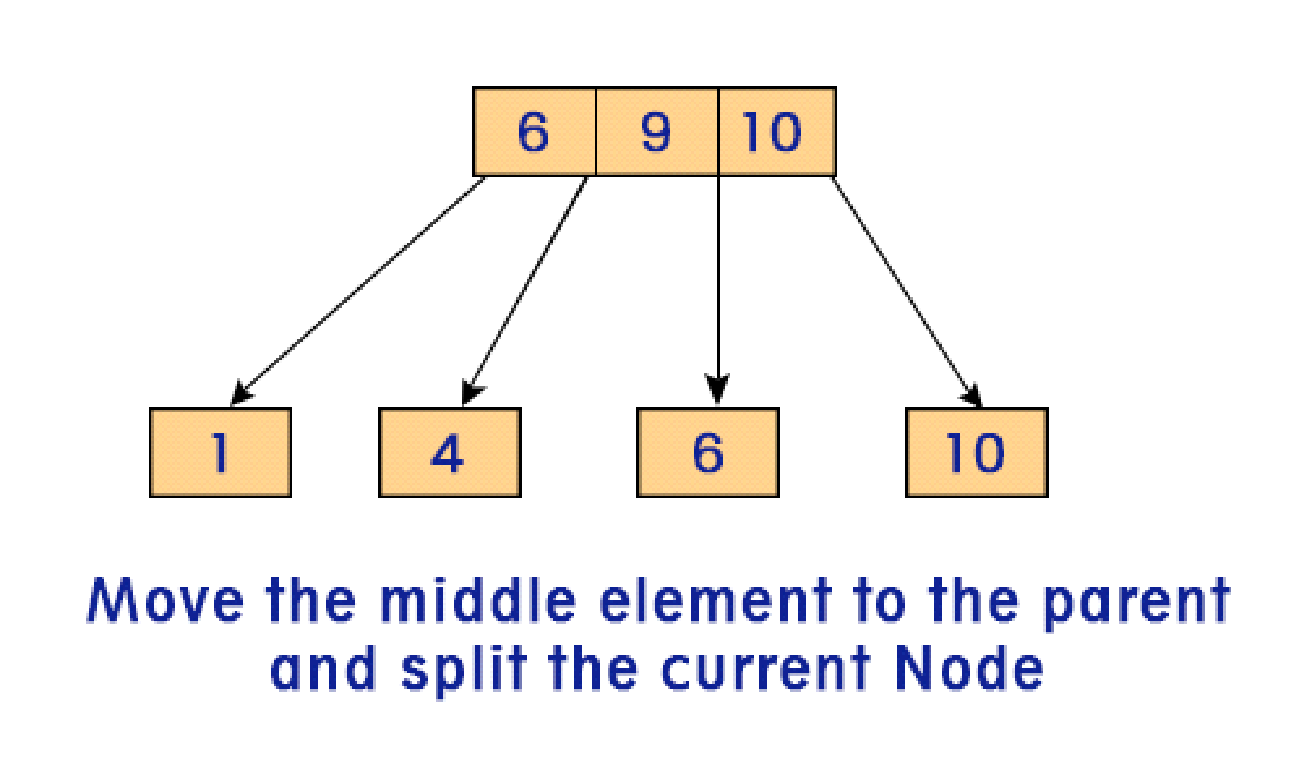
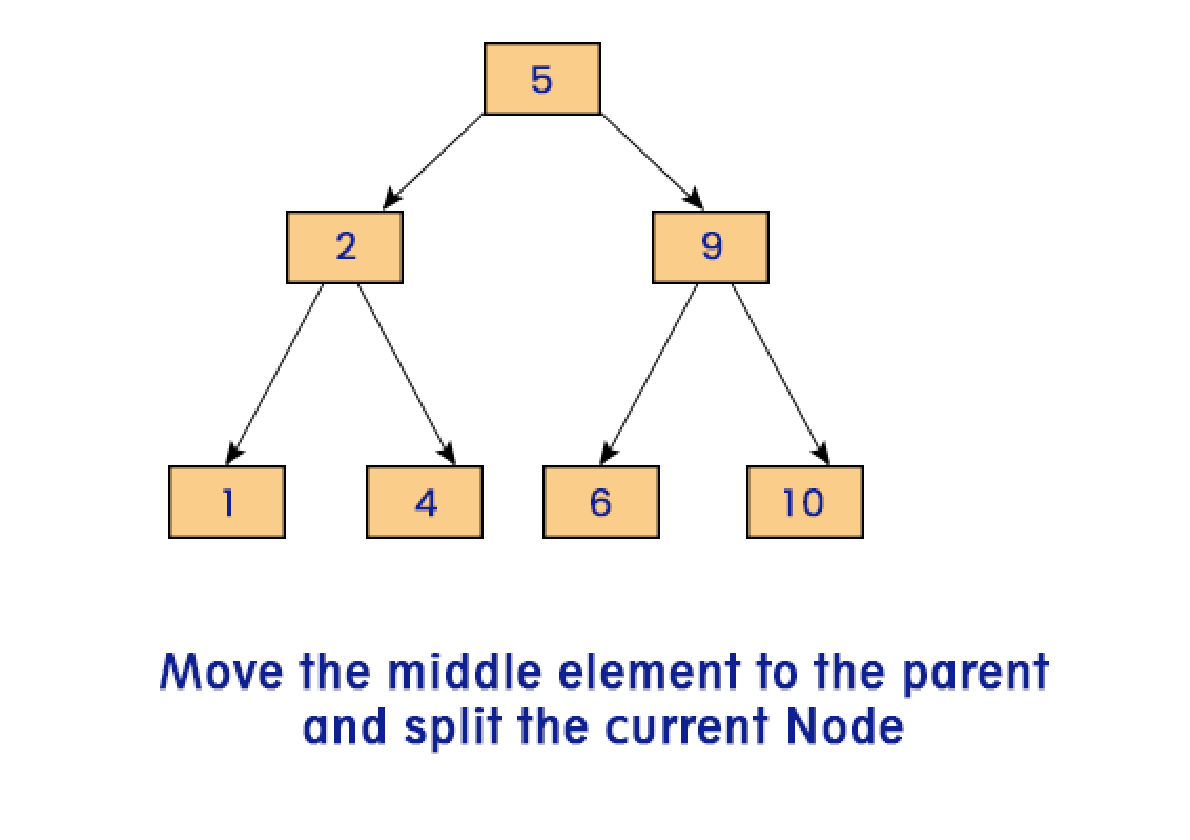
Deletion
While deleting any node from the 2-3 tree (3 order B-tree), the value to be deleted is simply replaced by the next value from the in-order traversal of the 2-3 tree.
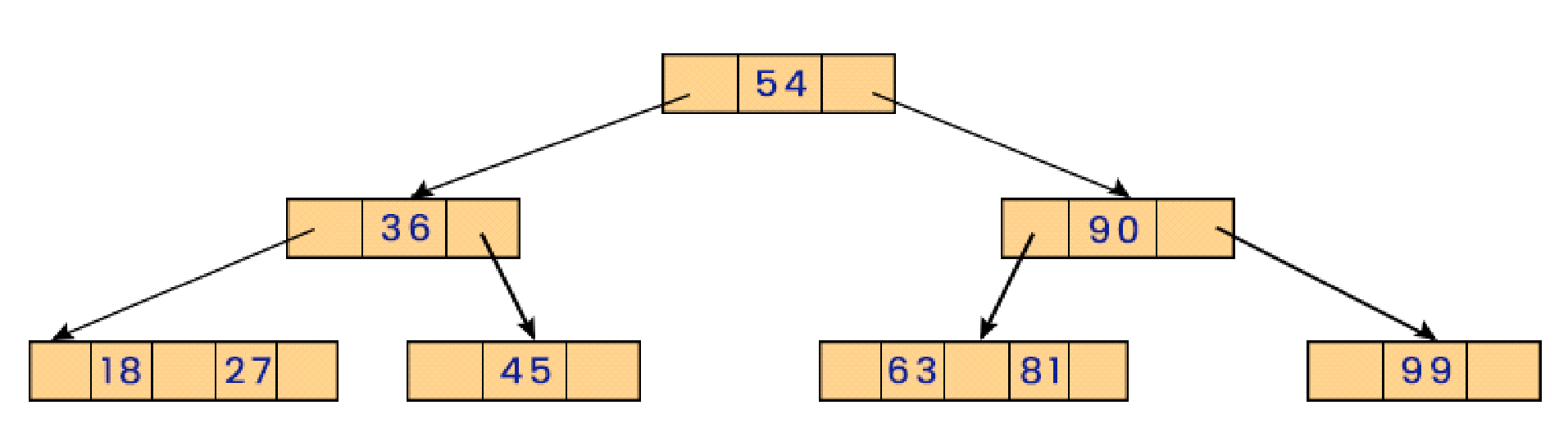
If the node is left empty after the deletion of the value, it is merged with the adjacent node. Using examples can help us better understand the omission of values from a 2-3 tree. Let us look at the following tree and delete the two values, 54 and 79.
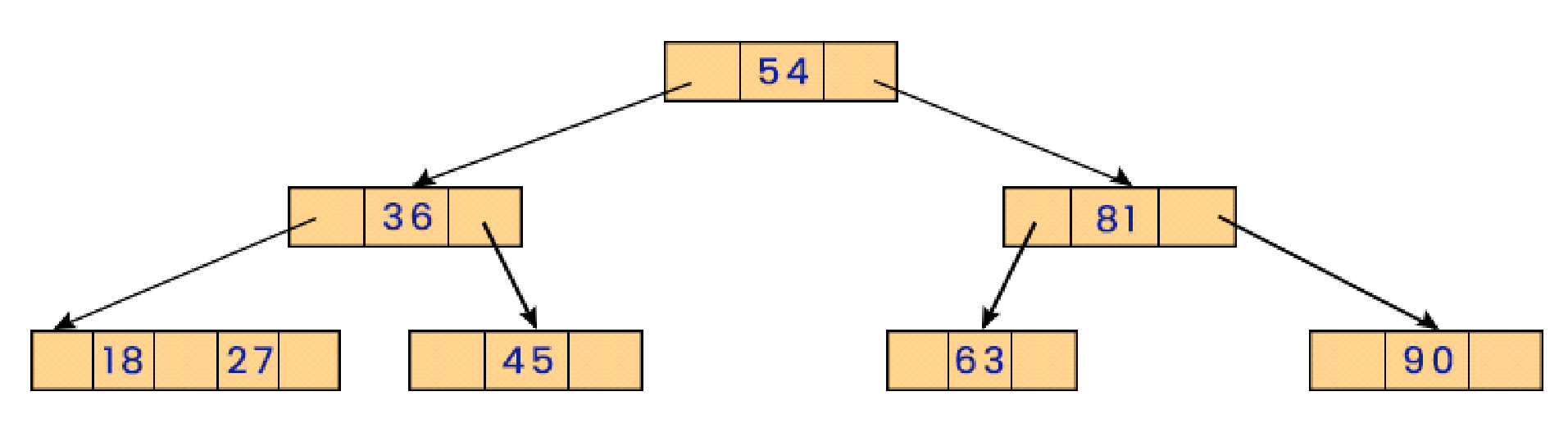
To delete the data item with value 54, first exchange its value with its successor in in-order traversal, which would be 79. Now the data item to be deleted is present in the leaf node, and hence easily remove the data item.
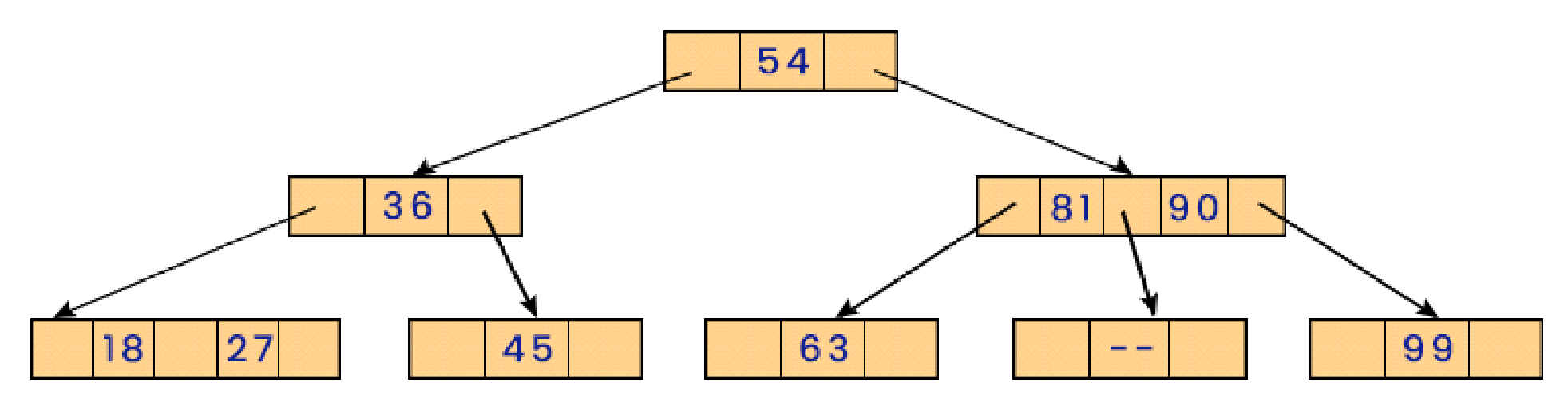
Now to delete the next item, 79, from the tree, exchange it with its successor to bring it to the leaf node and hence delete it from the tree.
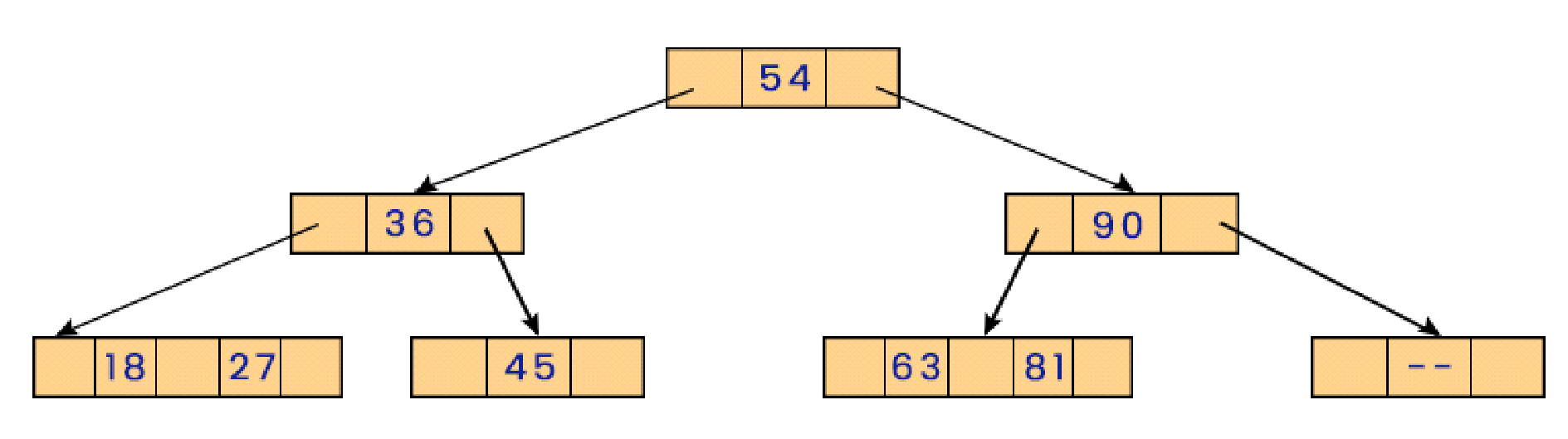
But here, after removing the data item 79 from the tree, the node left behind is empty, and as we know that a 2-3 tree can never have any empty node, hence bring down the lowest data element from the parent node and merge it with its left adjacent node.
In the given 2-3 tree below, delete the values: 69, 72, 99, 81 from it.
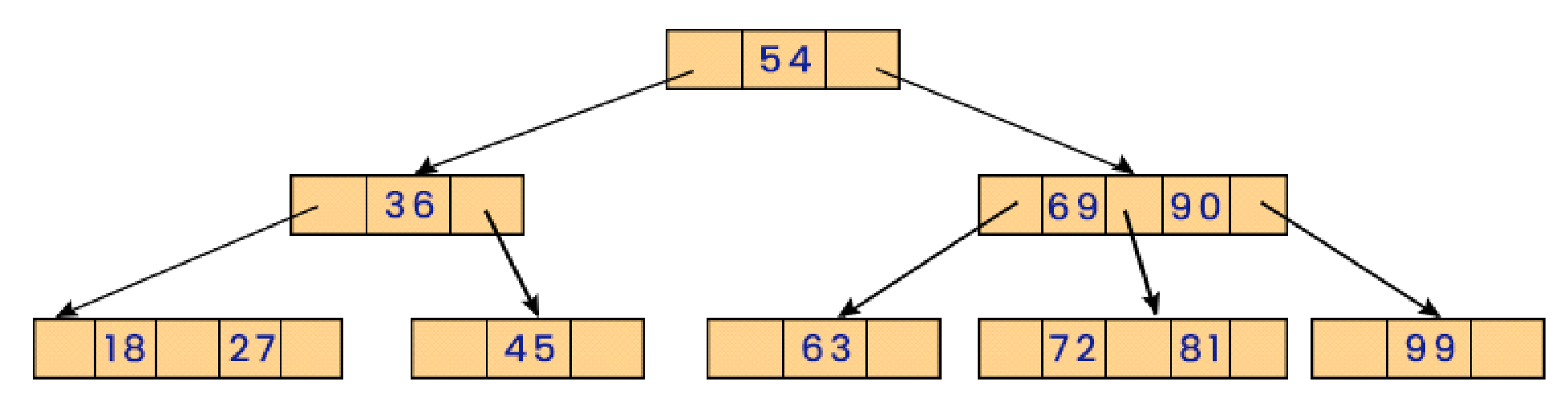
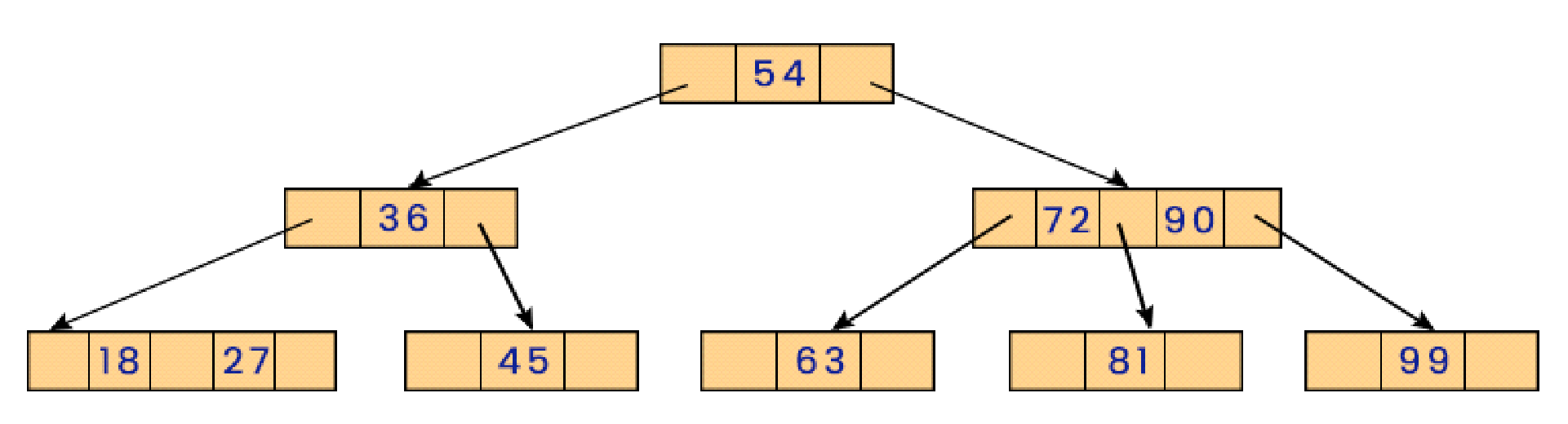
After deletion of Node item 69.