Application of Stack in Data Structures

In this article, we will discuss all the different applications of stack.

What is meant by stack?

The stack is a non-primitive linear data structure in which the insertion of the new data item and deletion of the existing data item is done only from one end, known as the top of the stack (TOS).

The top element is the most accessible element in a stack, and the bottom element is the least accessible element. The stack is widely used in different applications where data access follows the First In Last Out (FIFO) or Last In Fast Out (LIFO) mechanism.

The main applications of Stack data structure are listed below:

• Recursion
• Managing Function Calls
• Data Reversing
• Arithmetic Equations Evaluation
• Algorithms (Depth First Search)
• Undo and Redo Operations
• Backward and Forward operations in Browser

Let us discuss the above applications of the stack data structure in brief:

1. Recursion – Recursion is defined as defining anything in terms of itself. It is the most powerful tool in the programming language. A function is called recursive if the statement in the function’s body calls the same function or another function.

Properties of Recursion:

• Base Criteria – Base criteria defines the condition for the function calls to stop. If the base criteria are not defined within the function’s body, it will result in infinite function calls, and the program will never terminate itself.
• Progressive Approach – The function calls or recursion should follow the progressive approach means on each function call, the program or function should come close to the base criteria. Otherwise, it will reach a non-terminating state.
  
  Let us now see how the stacked is used in recursion. To understand the following, we have taken an example to calculate the sum of n natural numbers using recursion, and the code of the same is given below

// Function to calculate the sum of n natural numbers using recursion
int sum_upto_n(int n)
{
    if (n <= 1) // Base condition
        return n;
    return n + sum_upto_n(n - 1); // Recursive function call
}

Suppose the value of n is 5. Now, let’s see how all the function calls are managed and evaluated.

Function calls	Evaluation	Operations	Activation record (Stack)
Sum_upto_n(5)	5 + sum_upto_n(5-1)	Push()	5 + sum_upto_n(5-1)
Sum_upto_n(4)	4 + sum_upto_n(4-1)	Push()	4 + sum_upto_n(4-1) 5 + sum_upto_n(5-1)
sum_upto_n(3)	3 + sum_upto_n(3-1)	Push()	3 + sum_upto_n(3-1) 4 + sum_upto_n(4-1) 5 + sum_upto_n(5-1)
sum_upto_n(2)	2 + sum_upto_n(2-1)	Push()	2 + sum_upto_n(2-1) 3 + sum_upto_n(3-1) 4 + sum_upto_n(4-1) 5 + sum_upto_n(5-1)
sum_upto_n(1)	return 1	-	2 + sum_upto_n(2-1) 3 + sum_upto_n(3-1) 4 + sum_upto_n(4-1) 5 + sum_upto_n(5-1)
	return 2 + 1 = 3	Pop()	3 + sum_upto_n(3-1) 4 + sum_upto_n(4-1) 5 + sum_upto_n(5-1)
	return 3 + 3 = 6	Pop()	4 + sum_upto_n(4-1) 5 + sum_upto_n(5-1)
	return 4 + 6 = 10	Pop()	5 + sum_upto_n(5-1)
	return 5 + 10 = 15	Pop()	Empty stack

From the above table, we can clearly understand how the recursion is managed using the stack data structure.

2. Managing function calls – The stack data structure is used to manage function calls. When multiple functions call each other, the stack plays a crucial role in managing all the function calls and giving the correct result.

Let us assume there are three functions A, B, and C. Assume that initially, function A is called by the main function, and in the body of the function A, a statement calls the function C, and in the body of function C, a statement calls the function B.

int main()	int A()	int B()	int C()
{	{	{	{
// Statement 1 of main	// Statement 1 of A	return X++;	// Statement 1 of C
X = A() ; // calling Function A	X = C(); // calling Function C	}	X = B(); // Calling function B
cout(X);	X = X + 10;		X = X % 10;
return 0;	return X;		return X;
}	}		}

When the main function calls the function A, the statements of the main function below the function call are pushed into the stack for later evaluation. Also, the function A calls the function B, and the statements of function A below the function call are pushed into the stack. Same for the function C, when the function C calls the function B, the statements below the function calls are pushed into the stack. Function B will not call any other function and will return the value of X after incrementing its value by 1. And the control will be again transferred to function C, and function C will execute all the remaining statements and return the value of X after evaluation. After that, the control will be transferred to function A, and it will execute all the remaining statements and return the value of X to the main function. In the end, the control will be again transferred to the main function, and it will print the value of X, and the program will terminate.

Different states of the stack are shown below:

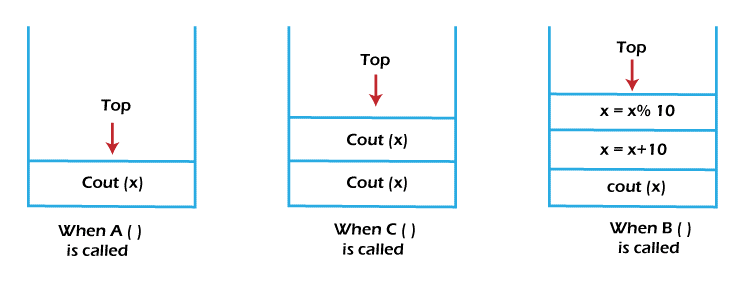
The pop operation is performed one by one.

We can conclude from the above figure that function A will only be complete after the completion of function C and function C will only be completed after the completion of function B. The main function will be completed last.

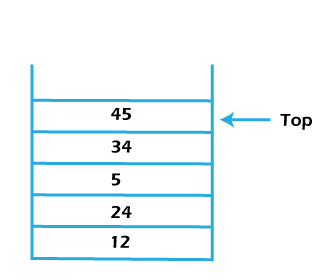
3. Data reversing – The stack data structure is used to reverse a set of values or data. The method of doing the same is explained below:

Consider a set a value = {12, 24, 5, 34, 45}

Now we push all the values one by one, and the stack after pushing all the values will look like as shown in the figure:

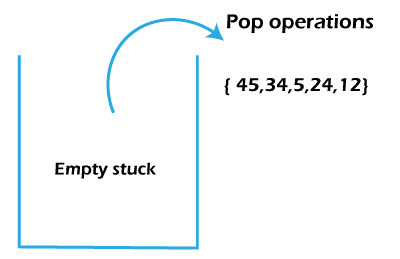
Now, we will perform the pop operation until our stack becomes empty. After completing all the pop operations, the order of the data is reversed, as shown in fig.

Conclusion – To reverse a set of values or data using a stack data structure, we need to push all the elements one after one and perform a pop operation until the stack is empty.

4. Arithmetic Expression Evaluation – As we know, the arithmetic expression is basically represented in three notations: Prefix, Infix, and Postfix (Polish) Notation.

The stack data structure is used to solve arithmetic operations. Postfix notation is the most suitable notation for the computer to solve or calculate any expression. It is the universally accepted notation for designing the Arithmetic and Logical Unit (ALU) of the CPU. Any expression entered into the computer is first converted into Postfix (Polish) notation, stored in a stack, and then evaluated.

The stack data structure is used to convert the expression written in one notation into another notation.

You can learn the conversion of expression by clicking the below links:

Infix Notation to Postfix Notation

< https://www.tutorialandexample.com/data-structure-infix-to-postfix-conversion >

Prefix Notation to Postfix Notation

< https://www.tutorialandexample.com/data-structure-prefix-to-postfix-conversion >

Now, let us look at how the expressions are evaluated using the stack data structure:

Q. Evaluate the following postfix expression:

P: 8 2 3 * 1 / + 4 1 * 2 / +

Ans. To solve the above expression, we scan all the symbols one by one, and for the values scanned, we perform the push operation, and for every arithmetic symbol, we perform the pop operation. The number of pop operations depends on the type of arithmetic symbol scanned, whether it is unary, binary, or tertiary. Here, we need to know that the top element of the stack is always operand 2, and the next element is operand 1. For any arithmetic symbol, we calculate as [operand 1 (arithmetic symbol) operand 2].

	Symbol Scanned	Operation performed	Stack
0.			Top -> Null
1.	8	Push (8)	Top -> 8
2.	2	Push (2)	Top -> 2, 8
3.	3	Push (3)	Top -> 3, 2, 8
4.	*	Pop () = 3 Pop () = 2 2 * 3 = 6 Push (6)	Top -> 6, 8
5.	1	Push (1)	Top -> 1, 6, 8
6.	/	Pop () = 1 Pop () = 6 6 / 1 = 6 Push (6)	Top -> 6, 8
7.	+	Pop () = 6 Pop () = 8 8 + 6 = 14 Push (14)	Top -> 14
8.	4	Push (4)	Top -> 4, 14
9.	1	Push (1)	Top -> 1, 4, 14
10.	*	Pop () = 1 Pop () = 4 4 * 1 = 4 Push (4)	Top -> 4, 14
11.	2	Push (2)	Top -> 2, 4, 14
12.	/	Pop () = 2 Pop () = 4 4 / 2 = 2 Push (2)	Top -> 2, 14
13.	+	Pop () = 2 Pop () = 14 14 +2 = 16 Push (16)	Top -> 16
14.	NULL	Pop () = 16	Top -> NULL

The above method shows how an expression written in postfix notation is evaluated using the stack data structure. For any numeric value, we perform a push operation. For any arithmetic symbol, we pop operations, then perform the calculation and push operation to push the calculated value into the stack.  In the last step, the symbol scanned is NULL. Hence, we perform the pop operation for the last time to get the result.

5. Algorithms (Depth First Search) – The Depth First Search (or Traversal) is used to search for an element in a Tree or Graph data structure. We do not have cycles in the tree, but we can have cycles in the graph so we may come to the same node again. While traversing a graph containing cycles, we use a Boolean visited array.

The standard DFS algorithm categorises each vertex as visited or not visited. A stack is used to implement the DFS algorithm. There are four steps to be followed by the DFS algorithm, which are given below:

1. Starts by pushing any of the Graph’s vertices or Tree’s node into the stack
2. Takes the top item of the stack and adds it to the visited list
3. Creates a list of all the adjacent vertices of that node. And now adds one of the adjacent nodes which is not in the visited list to the top of the stack
4. It keeps repeating step2 and 3 until the stack is empty.

To learn about the implementation of DFS, you can click on the given link below:

https://www.tutorialandexample.com/dfs-depth-first-search-algorithm-in-ds

Now, let us look at the mechanism behind the DFS with an example.

Q. Consider the following graph and perform DFS on it:

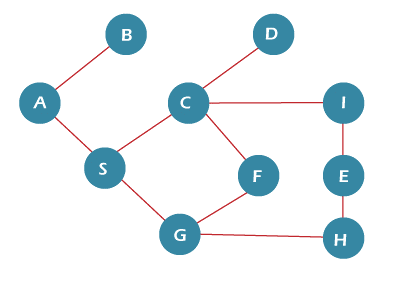
Ans.

S no.	Current Node	Adjacent node	List of Visited node	Operation	Stack	Remarks
0.			Null	Push(A)	Top -> A	Selecting node-A as the starting node
1.	A	B, S	A	Push (B)	Top -> B, A
2.	B	A	A, B	Pop ()	Top -> A	As we have no unvisited adjacent node of B, we will pop it from the stack and move to the previous, i. e., A.
3.	A	B, S	A, B	Push (S)	Top -> S, A	Here, S is the only unvisited adjacent node.
4.	S	A, C, G	A, B, S	Push (C)	Top -> C, S, A	We first find the unvisited adjacent node and add it to the stack. Here C and G both are unvisited, and we can add any of both as per our choice.
5.	C	S, D, F, E	A, B, S, C	Push (D)	Top -> D, C, S, A	Here, F and D are both unvisited, and we select D.
6.	D	C	A, B, S, C, D	Pop ()	Top -> C, S, A	No, unvisited adjacent node. Hence, we pop D from the stack.
7.	C	S, D, F, E	A, B, S, C, D	Push (F)	Top -> F, C, S, A	Here, only F is unvisited, and we push it into the stack.
8.	F	C, G	A, B, S, C, D, F	Push (G)	Top -> G, F, C, S, A	Only G is unvisited, and we push it into the stack.
9.	G	S, F, H	A, B, S, C, D, F, G	Push (H)	Top -> H, G, F, C, S, A	Only H is unvisited, and we push it into the stack.
10.	H	E, G	A, B, S, C, D, F, G, H	Push (E)	Top -> E, G, F, C, S, A	Only E is unvisited, and we push it into the stack.
11.	E	I, H	A, B, S, C, D, F, G, H, E	Push (I)	Top -> I, E, G, F, C, S, A	Only I is unvisited, and we push it into the stack.
12.	I	C, E	A, B, S, C, D, F, G, H, E, I	Pop ()	Top -> E, G, F, C, S, A	No unvisited adjacent node. We will pop it from the stack. Here, have visited all the nodes, so we will pop all the nodes and check whether any of the nodes are left unvisited or not until the stack is empty.

We will be adding the visited node in the output sequentially:

Output = A, B, S, C, D, F, G, H, E, I

The above table shows us how the stack is used to implement Depth First Search (or Traversal) Algorithm.

6. Undo and Redo Operation –

• Undo Operation – The undo operation helps us to retrace our steps and actions than being able to go back to the previous state. The undo operation is crucial to revert our mistake instantaneously.
• Redo Operation – The redo operation helps us to revert or restore the previously undone task using the undo operation. This feature is also referred to as a reverse undo.

The undo and redo operations are implemented using a separate stack. Let’s say the stack used to implement the undo operation is ‘undo stack’, and the stack used to implement the redo stack is ‘redo stack’.  The undo stack stores all the actions performed by us. The latest performed action will be found at the top of the stack.

When we perform undo operations, we pop the top action present in the undo stack and push it into the redo stack.

And when we perform redo operations, we pop the latest undone action (which is present at the top of the redo stack) from the redo stack and push it to the undo stack. The push and pop operations are performed on undo and redo stacks for each undo and redo operation in the same manner.

Assume that we have performed some actions and the states of Undo and Redo Stacks before performing any undo and redo operation are look like as shown in the figure below:

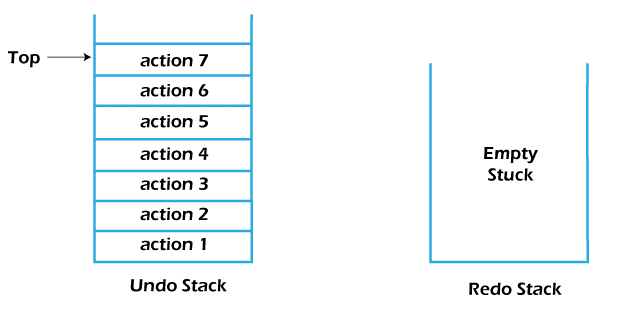
The states of the Undo and Redo stacks after performing three undo operations:

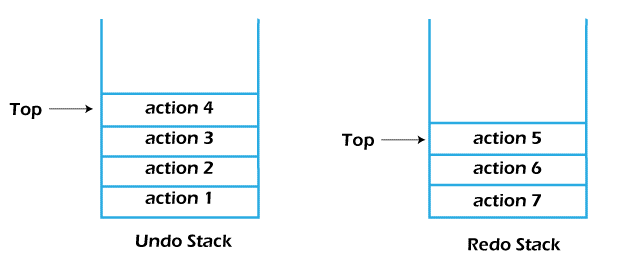
The top three actions are popped from the Undo stack and pushed into the Redo stack in order.

The states of the Undo and Redo stacks after performing two redo operations:

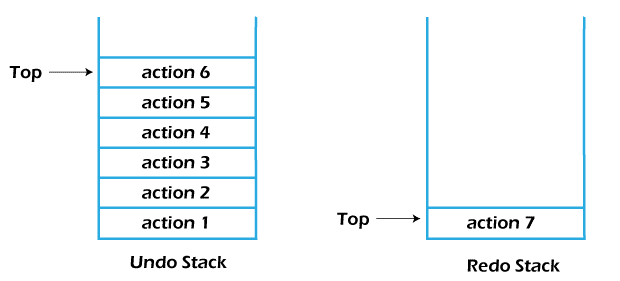
The top two actions are popped from the Redo stack and pushed into the Undo stack in order.

The states of the Undo and Redo stacks after performing some actions:

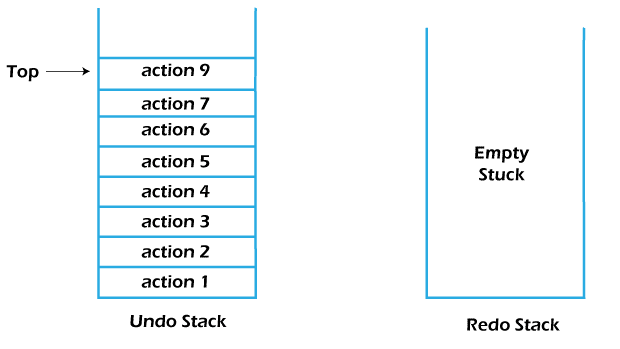
New actions are pushed into the Undo stack in order.

Remark - When we start performing actions after performing some undo operations, we can no longer perform the redo operations because the redo stack will get automatically empty, which is also shown in the above figure.

7. Forward and Backward Operations in Browser – The forward and backward operation is implemented using two separate stacks called Forward and Backward Stacks.

Backward Operation – The backward operation is used to revisit the previously visited site.

Forward Operation – The forward operation is used to revisit the latest back-warded site.

When we visit sites or pages, the addresses are stored in the backward stack.

When we perform backward operations, the top address of the Backward Stack is popped and pushed into the Forward Stack.

When we perform forward operations, the top address of the Forward Stack is popped and pushed into the Backward Stacks. The push and pop operations are performed on the Forward and Backward Stacks in the same manner for each forward and backward operation.

The states of the forward and backward stacks after visiting some sites and without performing any forward and backward operations are shown in the figure below:

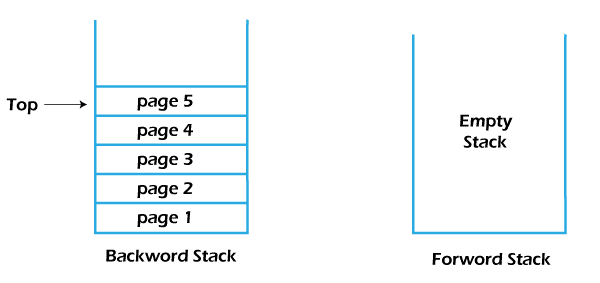
The states of the stacks after performing two backward operations:

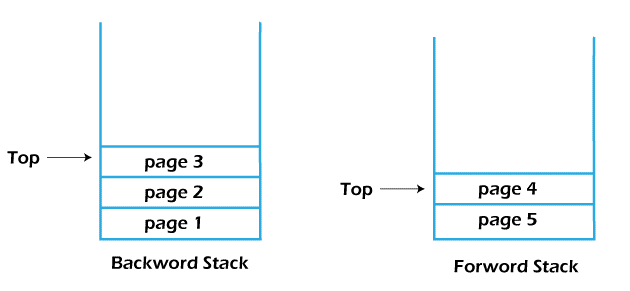
The top addresses of the backward stack are popped and pushed into the forward stack in order.

The states of the stacks after performing one forward operation:

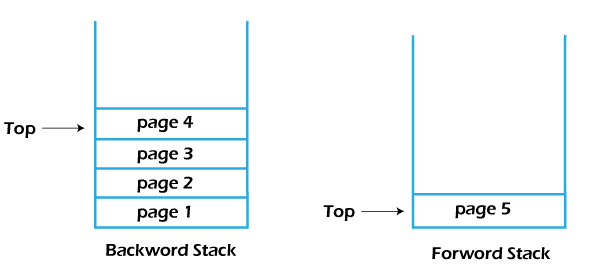
The top address of the forward stack is popped and pushed into the backward stack, also shown in the figure.

The states of the stacks after visiting new sites (or pages):

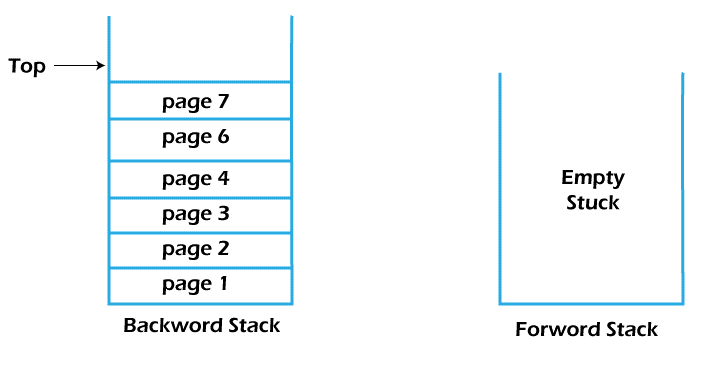
The new addresses are pushed into the backward stack, the forward stack becomes empty, and we can no longer visit the pages whose addresses vanished from the forward stack.