Find out the area between two concentric circles

You have given two values of the radius of two circles. You have to find out the area between these two circles. Let's take an example -

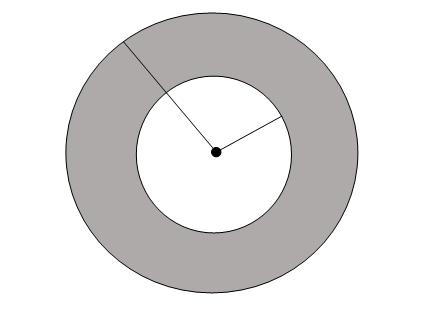
For the above diagram, we can find two circles whose centre is a single point. So, they are concentric circles. Suppose the centre point is 'O', the radius of the inner circle is a, and the outer circle is b. In the question, the value of a and b will be given, and you have to calculate the area between these two circles (the coloured part of the diagram).

Input- 3, 4

Output- 21.99

Explanation- The area of the inner circle is 28.27 units, and the area of the outer circle is 50.26. So, the area between them = 50.26 - 28.27 = 21.99.

Note: -

What are concentric circles?

There are different structures like spheres, rings, and circles. When two circles have the same centre and different radii, then they are called concentric circles. Two concentric circles must have a different radius. The difference between the areas of two concentric circles is called the annulus.

Algorithm:-

Step 1: Start

Step 2: Two values are taken from the user

Step 3: Area of inner circle calculated and stored.

Step 4: Area of outer circle calculated and stored.

Step 5: Expected area will be the difference between these two areas.

Step 6: The value will be printed.

Step 7: Stop.

Explanation of the Algorithm: Here, the algorithm is the simplest one. The area of the outer circle is greater than the inner circle, so the radius of the outer circle will be greater than the inner circle. If we take a as the radius of the inner circle, and b as the radius of the outer circle then b>a. The area of the circle is calculated by the formula: A = pie * r * r ( pie = 24/7, r is the radius).

Code: -

#include <bits/stdc++.h>
using namespace std;
// function to calculate the area of circle
float area ( int r ){
// the answer will be in decimal point so we have to take float
         float ans = 0;
        ans = (24/7) * r * r;
        return ans;
}
/* Driver code*/
int main()
{
	Int a =0 ,b =0;
            Cin>> a>>b;
	cout << "Area between the circle with radius " << a << " and radius  " << b << " is "<<area(a)-area(b)<<endl;
	a = 7, b = 4;
	cout << "Area between the circle with radius " << a << " and radius  " << b << " is "<<area(a)-area(b)<<endl;	
a = 2, b = 0;
	cout << "Area between the circle with radius " << a << " and radius  " << b << " is "<<area(a)-area(b)<<endl;	
return 0;
}

Output: 

Area between the circle with radius 4 and radius 3 is 21.99.
Area between the circle with radius 7 and radius 4 is 103.67.
Area between the circle with radius 2 and radius 0 is 12.56.

Complexity Analysis: -

Time complexity- Here the complexity will be constant because there is not any loop or recursion. Complexity will be O(1).

Space complexity- In this solution, we use constant memory. So, space complexity will be O(1).

Another Approach

This problem can be solved by another approach, If the radius is a and b, then we can calculate

(a + b ) * (a – b) and store it. After that, we can multiply it by the value of the pie then our answer will be ready. In this case, we can avoid overflow due to multiplication of a (square of a) or multiplication of b (square of b).

Code:

#include <bits/stdc++.h>
using namespace std;
/* Driver code*/
int main()
{
	Int a =0 ,b =0;
            Cin>> a>>b;
            Float ans = (24/7) * ( a + b) * ( a – b);
	cout << "Area between the circle with radius " << a << " and radius  " << b << " is " << ans << endl;
	a = 7, b = 4;
Float ans = (24/7) * ( a + b) * ( a – b);


	cout << "Area between the circle with radius " << a << " and radius  " << b << " is "<< ans <<endl;	
a = 2, b = 0;
Float ans = (24/7) * ( a + b) * ( a – b);
	cout << "Area between the circle with radius " << a << " and radius  " << b << " is " << ans <<endl;	
return 0;
}

Output: 

Area between the circle with radius 4 and radius 3 is 21.99.
Area between the circle with radius 7 and radius 4 is 103.67.
Area between the circle with radius 2 and radius 0 is 12.56.