What Is Graph Data Structure

A graph is generally a set of vertices and edges or border that is mainly used to join these vertices. A graph is basically pictured as a cyclic tree in which we can easily support the vertices or the nodes rather than supporting the parent child table. A graph can be easily defined as a collection of an ordered set that can be represented as G(V, E) where V(G) portrays the set of vertices and on the other hand E(G) represents the set of  edges. They are particularly used to join the vertices. The graph data structure can be further divided into two categories that are:-

• Directed graph data structure
• Undirected graph data structure

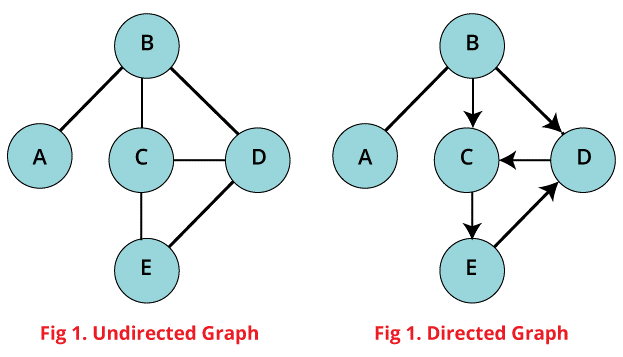
I. Directed graph data structure

A graph in particular can either be directed or un-directed. Directed graph data structure contains a sequential pairs of vertices

II. Undirected graph data structure

An undirected graph can be described as the one, in which the set of vertices are in random pairs. In this, the edges are not connected with any of the directions.

There is wide range of components present in graph data structure, which we are going to discuss in this section of the article.

1. PATH

It can be described as a pattern of nodes or vertices that is followed to reach terminal V from the initial node.

2. CLOSED PATH

A specific path is called as a closed path when the initial node and the terminal node collide implying that they are the same.

3. SIMPLE PATH

If all the nodes or vertices of the graph are well-defined such that V₀=V_N, then these type of path is called as the simple path.

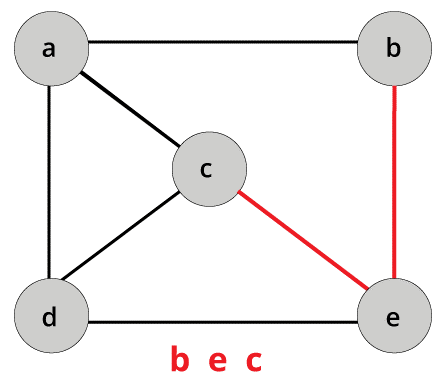
4. CYCLE

It can be defined as a specific path in which the vertices or the nodes of the graph is not repeated except the first and the last nodes or vertices.

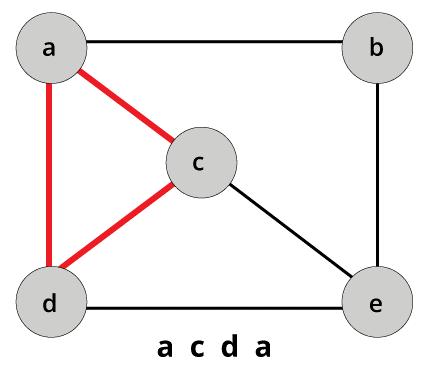
5. CONNECTED GRAPH

It is a kind of graph in which there is some sort of path present between every two vertices or nodes. There doesn’t exist any kind of remote vertices.

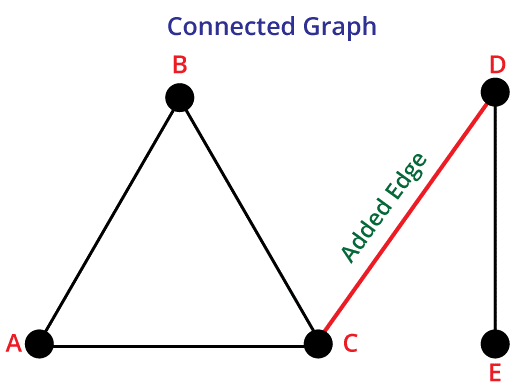
6. WEIGHTED GRAPH

In this, each edge is associated with some sort of data such as length or the weight. Generally, the weight of an edge can be represented as w(e) and it must be a positive value that particularly points to the negotiation of the edge.

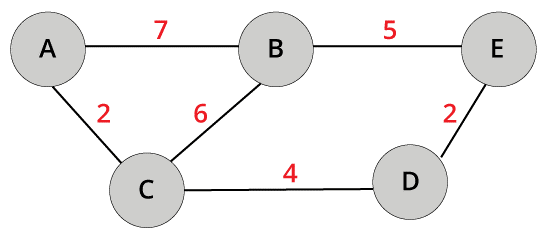
7. DIGRAPH

It is a directed graph in which each and every edge of the graph is instructed with a specific direction and the negotiation can be done only in a particular direction.

8. LOOP

An edge which contains similar end points is called a loop.

9. ADJACENT NODES

When two given nodes such as p and q are interconnected through same edge e, then these nodes p and q are known as the neighbours or adjacent nodes.

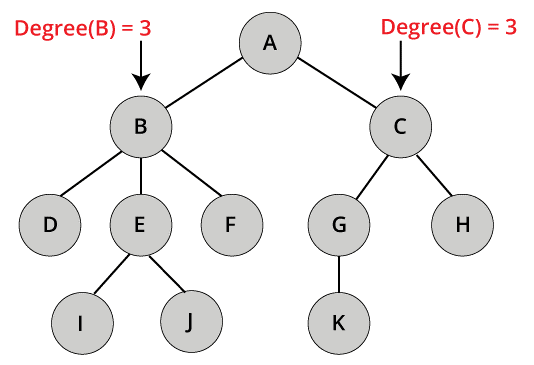
10. DEGREE OF THE NODE

A degree of the node can be described as the total number of edges that are correlated with that specific node. A node which has 0 degree is called as an isolated node.

The graph data structure is generally acquired in computation to manage and resolve several other computation programming issues. They are practically used for resolving real-world problems where the problem-generating era is with the networks, such as telephone networks, LinkedIn, Facebook and several others. Practically, in the field of computation and technology, graphs are being used for their easy implementation of the directed or undirected graph notions from the theory that we have previously studied in mathematics. It is generally made of countless and potential order of vertices along with unordered pairs for an undirected graph. These specific pairs are recognized as the edges, links or lines in a directed graph but sometimes they are also referred as arrows or arcs. Based on whether they are denoted by integer indices or references, they can be categorized as internal or external graph elements.

TYPES OF GRAPH IN DATA STRUCTURE

Based on the position and structure of the nodes and vertices, there are different types of graph present in the data structure. In this specific section of the article, we are going to explain the various types of graphs present in data structure:-

• Null graph

The graph with the order zero is commonly known as the null graph. The phrase ‘null’ signifies the set of edges which is empty. It implies that a null graph doesn’t contain any edges and it only contains isolated vertices in the graph.

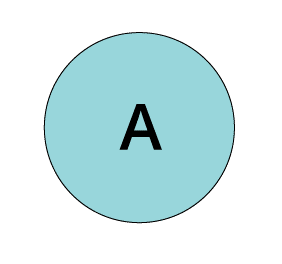
• Trivial graph

A graph is known as a trivial graph if and only if there is a single vertex present in it. Generally, it is made up of minimal number of vertices. It is made up of only a single vertex.

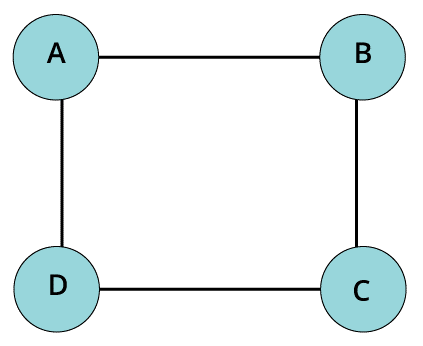
• Directed graph

When each edge present between the node and vertex has a designated or pre-defined direction, then it is called as the directed graph. Directed graph is also popularly known as digraph. The term directed basically means that every edge contains a defined direction implying it is already specified that from which node, it is starting and from which node it is ending.

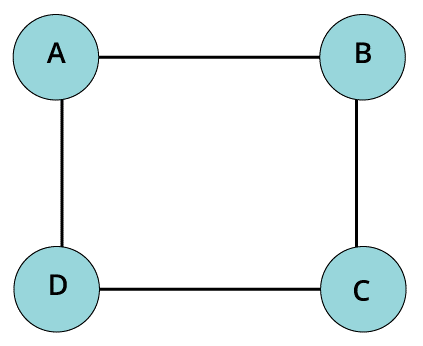
• Non-directed graph

When each edge present between the node and vertex doesn’t have a designated or pre-defined direction, then it is called as the non-directed graph. The term directed basically means that the direction of each edge cannot be determined. They don’t have a specific direction.

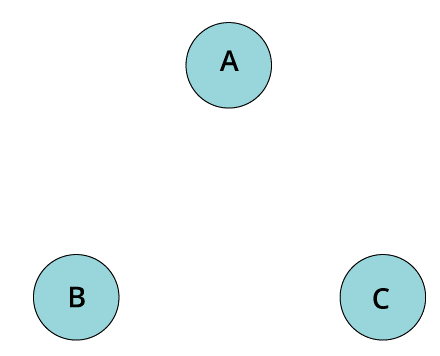
• Disconnected graph

A graph is generally termed as disconnected graph when the path between any pair of vertices is missing. More particularly, it means that we take up any given vertices and move from that particular vertex to other vertices in the graph, and then there will not exist any given path to move to that particular vertex.

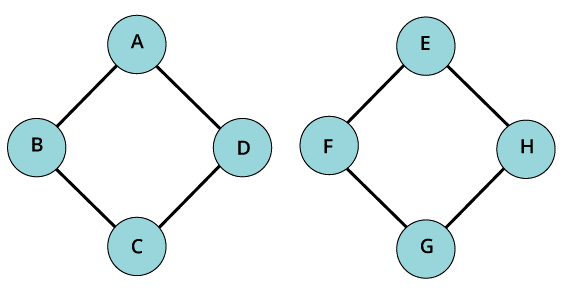
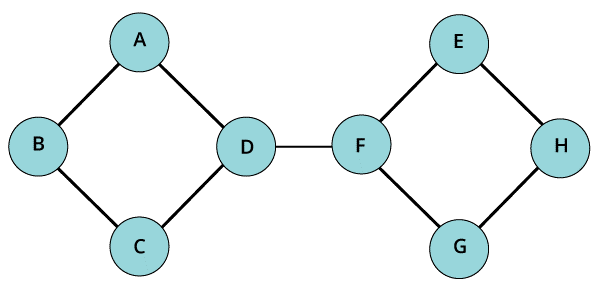
• Connected graph

When we call a particular graph as a connected graph, it signifies that there is slightly a single path in process between every duo of vertices. It implies that if we move from a particular vertex then we will be able to move from that particular vertex to other vertices as well.

• Regular graph

When we call a graph, a regular graph it simply means that all the vertices of that particular graph has the same degree. If all the nodes consists the value for the degree, then it is called as regular graph. Suppose, if a vertices have the degree ‘q’, then it will be termed as a “q-degree graph”.

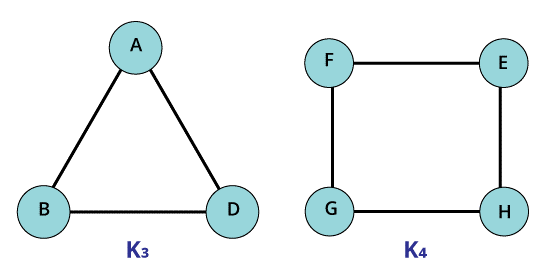
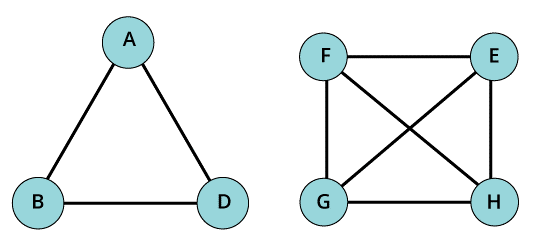
• Complete graph

A graph is termed as a complete graph, if and only if there must be an edge present between every pair of vertices. We can also say that all the vertices are correlated to the remaining vertices of the graph.

• Cycle graph

If a graph has many vertices and it is greater than three and the edges joins together in such a way that it forms a cycle, and then the graph is termed as a cycle graph. In this, the degree of the vertices is 2.

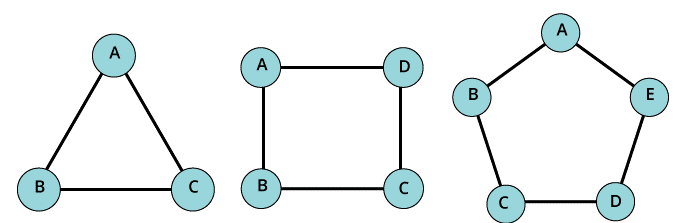
• Cyclic graph

In order to call a graph cyclic, it should have at least one cycle present in the graph. If the graph contains at least one cycle in it, then they are termed as cyclic graph.

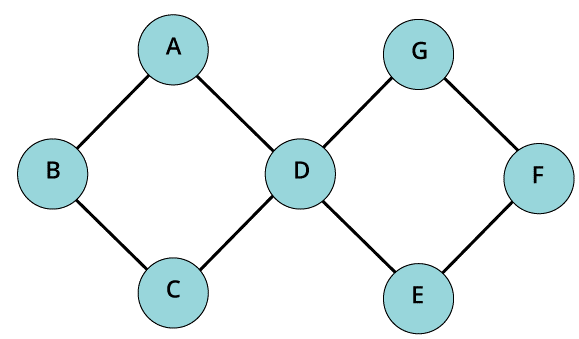
• Acyclic graph

A graph is termed as an acyclic graph if there doesn’t exist even a single cycle in the graph. Basically, it is the complete opposite of the cyclic graph.

• Finite graph

When the total number of edges and the total number of vertices present in the graph is countable, then the graph is known as the finite graph.

• Infinite graph

If the total number of edges and the total number of vertices present in a graph is unbounded or limitless, then it is called as the infinite graph.

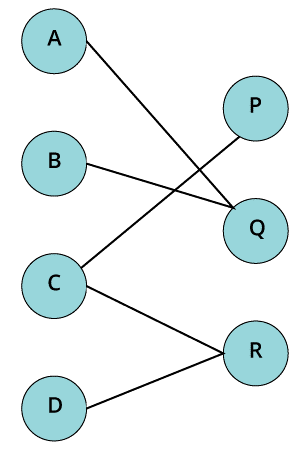
• Bipartite graph

A graph is termed as bipartite when it follows the basic conditions stated below:-

• All the vertices are distinguished in two sets of vertices that is X and Y.
• All the vertices present in the set X will only be joined to the vertices present in the set Y. It implies that it should not be connected to the same sets of edges.
• Both the sets that is X and Y should be different from one another which means they cannot contain same vertices in them.

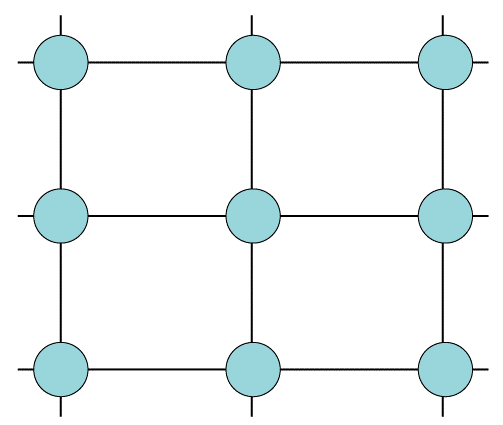
• Planar graph

A planar graph is a graph in which the graph can be drawn in a single horizontal surface with two edges, in which the two edges are crossing each other.

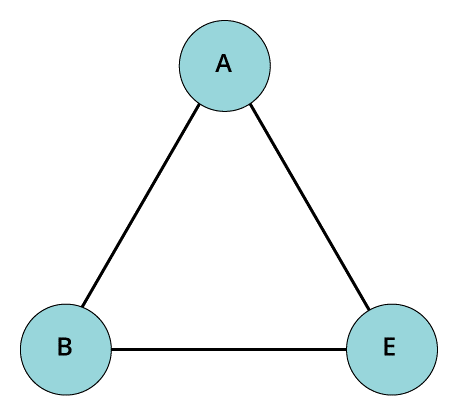
• Simple graph

When we call a graph simple, it implies that the graph doesn’t contain any kind of self-loops or parallel edges in it.

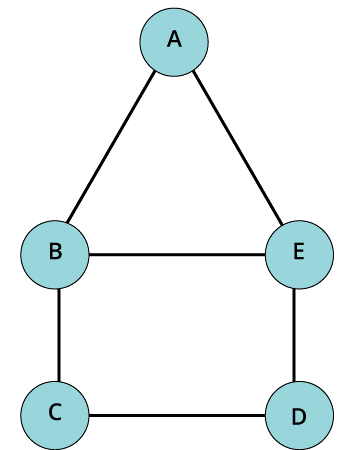
• Multi graph

A graph is termed as multi graph, when it doesn’t contain any kind of self-loops but it does contain parallel edges in them. If there exist more than one edge in between two given vertices, then that pair is called as the parallel edges.

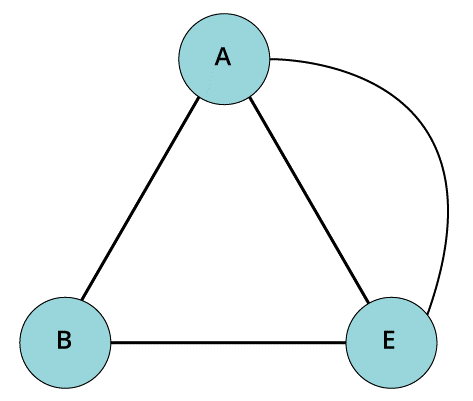
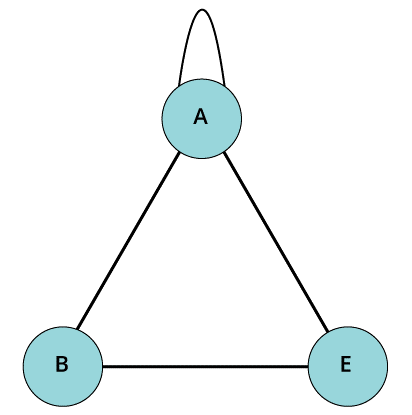
• Pseudo graph

If a graph contains no parallel edges but it does consist of self-loops, then it is termed as pseudo graph. Self-loop is nothing but an edge in the graph that begins from one of the graph’s vertices and if the also ends at the very same vertex.

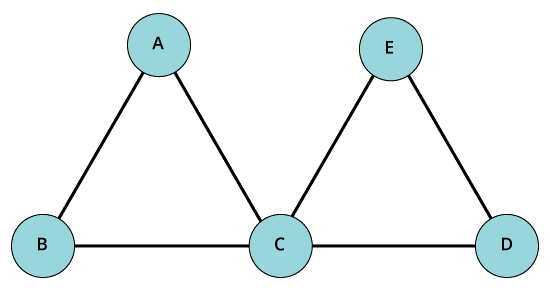
• Euler graph

When all the vertices present in a graph consists of an even degree, and then the graph is generally termed as Euler graph. The degree of vertex is usually the number of edges present in a specific vertex. For a graph to be termed as Euler it is necessary that all the edges should be of even number.

• Hamiltonian graph

There is a closed polygon in which the graph visits every individual vertex at least once without again visiting the edges. This kind of graph is called a Hamiltonian graph and the walk is called the Hamiltonian path. The Hamiltonian circuit is also sometimes referred as Hamiltonian Cycle.