Red-black Tree in Data Structures?
A type of binary tree which is known as the Red-Black tree, is a specialized and unique tree. What is the urgency or, to be more precise, the necessity of the same? Well, in this article, we are going to discuss that in detail.
So, the main aim of this type of tree is that we get more depth about the binary search tree as it is a part of it and exhibits its most likely nature and properties. In a typical binary search tree, it is believed that the nodes which are present on the left side should certainly be less in value as compared to the nodes present on the root or initial side.
The same goes for the right side as well, implying that the value of nodes present on the right side should be more than the initial or root values. Every single node that is a part or present on the tree is designated with a special color to make sure that at any given point, the tree is practical and sensible while carrying out any given operations, such as deletion, insertion, and several others.
Cases
In this section of the article, let’s look at the different scenarios of the red-black tree.
Case 1:
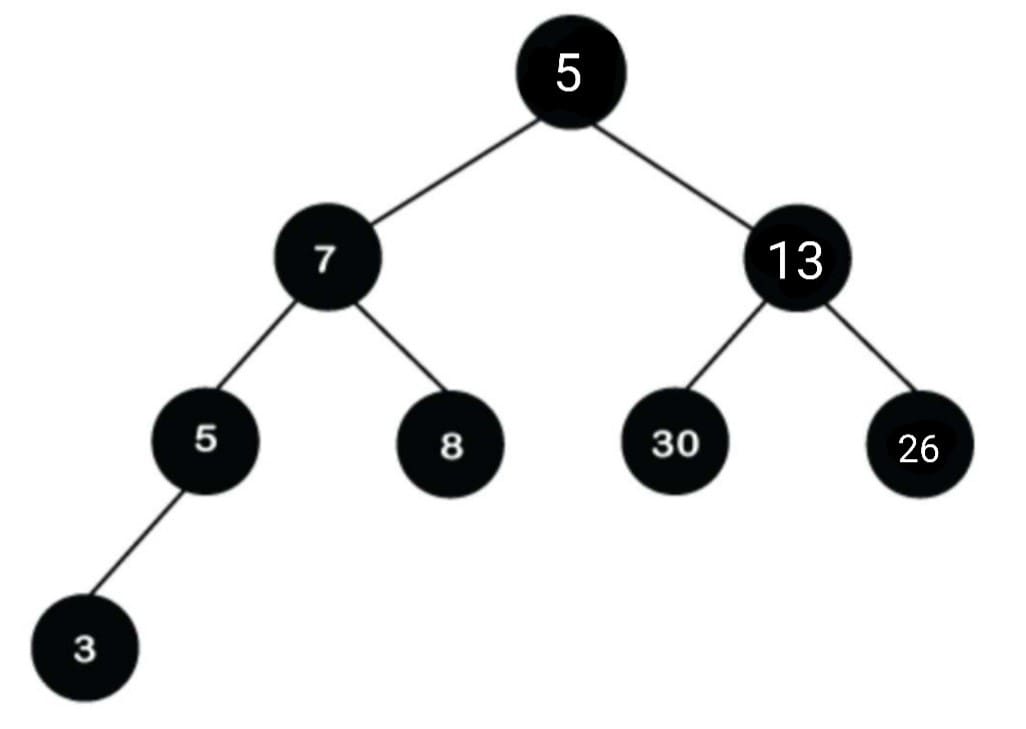
Let us assume that in the provided image above is a red-black tree, and in that, we have to find and explore a number, say 86. To do that, we have to first compare and verify the given number with the root or initial node. Now, from the given picture, we know that 86 is greater than the root node, which is 5, and so in that case, the searching will be initiated on the right subtree. Now, again 86 will be compared with 13. Here, we know that 86 is pretty much greater than 13, so we again shift to the right side.
As we move, we reach the leaf node, which is 26, and 26 is not equal to 86. Hence, it will display that the given element or number is not present in the designated tree. From this, we understood that after each operation, the search and exploration are further differentiated into half.
Case 2:
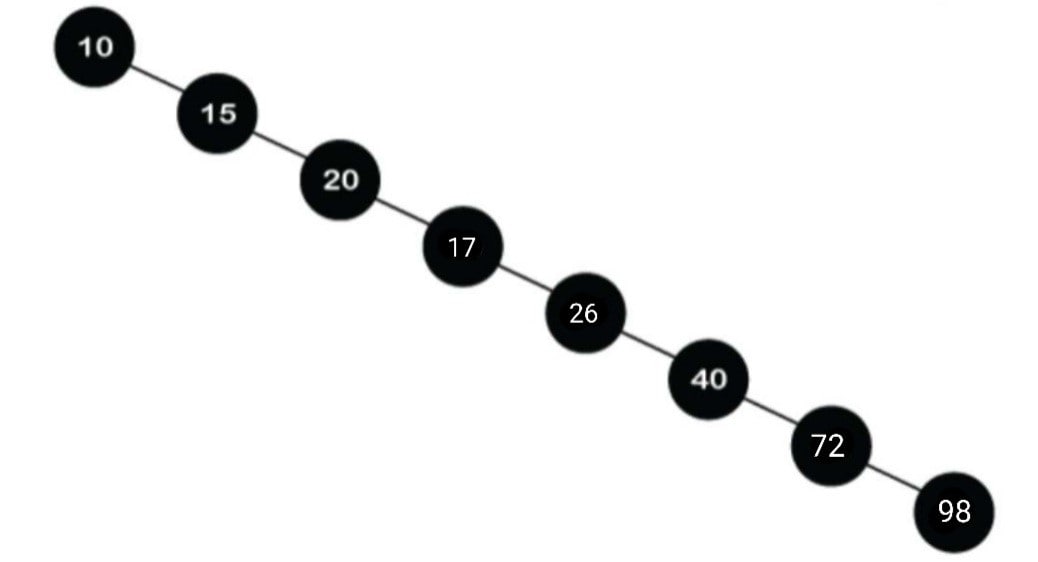
As we move on and discuss one more case for a better understanding of the algorithm, consider the image given below.
We have a binary search tree that is rightly skewed in nature. Now again, if in this tree we are given to find the number 86, then in this type of tree, we will compare the allotted number with every single value present on the tree above until and unless we find out the search element or in another case, we reach the leaf node. In the given binary search tree, the first one is in a systematic order, whereas if we look at the second one, we will find that the second one is in unsystematic order. From the above picture, we cease to believe that when we have two binary search trees which are balanced, they take quite less time to execute operations and produce results rather than an unsystematic one.
That is why we require the Red-black tree, and there is a need for them in the binary search trees as the red-black tree is self-organized and well-balanced. Do we know that the AVL tree is also height-balanced? Then why do we need the red-black tree? That is because the AVL tree needs a massive amount of rotations when it comes to large values and key functions. On the other hand, the red-black tree has the perfect characteristic where it takes a maximum of 2 rotations to organize a given tree.
The main part is that the AVL tree is strictly organized, whereas the red-black tree is partially organized, which means that we can mold the red-black tree according to our needs and requirements. Insertion and many other operations are also quite quickly performed if you compare them with the AVL tree. Another important fact that why it is called the red-black tree is because, in this type of tree, the nodes are either red or black.
Interesting facts
- Every single red-black tree turns out to be a unique case of the binary search tree.
- All the leaves that are present in the tree turn out to be black.
- The term black depth generally stands out for the number of black nodes from a specific node to the root node, which means the total number of black predecessors.
- The height of re – black tree is often calculated if it has n number of nodes, then h < = 2 log2 (n + 1).
- The height of the red-black tree, which is called the black tree, is generally calculated as the total number of black nodes on a specific route from the very initial, which is the root node to the leaf node, so the height of a red-black tree > = h/2.
Black height of the red-black tree
Black height is known as the number of black nodes present on a route from the very beginning, which is the root node to the very end, which is the leaf node. Nodes that are at the bottom, called the leaf nodes, are usually counted as the black ones. From looking at the characteristics of the red-black tree, we concluded that the height of a red-black tree could be written as h/2.
Can we call every single AVL tree a red-black tree?
The answer to this question is yes because every AVL tree can turn into a red-black tree as we can transform and color each node with either of the colors, which is red or black, but not every AVL tree can be a red-black one as they are very strictly coordinated and balanced. We all know that the red-black tree is not well-balanced.
Algorithm
searchElement (tree, value)
if tree - > info = value OR tree = NULL
return tree
else
if value < info
return searchElement ( tree - > left, value )
else
return searchElement ( tree - > right, value )
[ End of it ]
ENDComplexity
In this section of the article, we are going to discuss the complexity of the Red-Black tree in the best, worst and average cases. We will also encounter the space complexity of the same in this section.
Case
Time
Best case
O(log n)
Average case
O(log n)
Worst case
O(log n)
1. BEST CASE
In the best-case scenario, there is absolutely no rotation to insert some element, so only recoloring of the nodes takes place, so the best-case complexity of the Red-Black tree turns out to be O(log n).
2. AVERAGE CASE
The average case usually occurs when we have to take out the mean of all the possible scenarios, which is the sum of all the case / total number of cases. For this, the time turns out to be too long, so the time complexity, in this case, turns out to be O(log n).
3. WORST CASE
The worst case usually occurs when we know that the red-black tree acquires at least two numbers of rotations for insertion to take place. So, in the worst case, there will be at least two rotations for insertion to take place, and the worst-case complexity turns out to be O(log n).
Space Complexity
Space complexity is nothing but the whole amount of memory or space that a particular algorithm or program takes at the time of the execution of that program. The space complexity of the Red-Black tree is said to be O(n).
Implementation
/ *
We will create a class, and the name for the same will be a red-black tree.
*/
class Node_RB_Tree
{
// every element on the tree comprises of 4 elements each.
// Among everyone else the two members are for RB Tree named left and right node.
Node_RB_Tree_lft_node_addr, rt_node_addr;
Int node_info;
//the color of the xyz node is initialized with this: -
int colour_of_node;
/* Constructor is now being created */
public node_RB_Tree(int thenode_info)
{
this ( thenode_info, null, null );
}
/* Constructor for the node red black tree class */
Public node_RB_Tree( int thenode_info, node_RB_Tree lft, node_RB_Tree rt)
{
Left_node_addr = It;
Right_node_addr = rt;
Node_data = thenode_info;
Color_of_the_node = 1;
}
}
// A class will be built in which all the objs created will be of the red-black tree, and it will be named as RB_Tree
class RB_tree
{
private node_RB_Tree curr_node;
private node_RB_Tree parent_node;
private node_RB_Tree grand_node;
private node_RB_Tree great_node;
private node_RB_Tree header_node;
private node_RB_Tree node_null;
Static
{
node_null = new node_RB_Tree(0);
node_null.left_node_addr = node_null;
node_null.right_node_addr = node_null;
}
// We will now use the color coding method
/ * black – 1 red – 0 / *
static final int BLACK = 1;
static final int RED = 0;
// now we will create the constructor of the RB_Tree class
Public RB_Tree(int negInf)
{
header_node = new node_RB_Tree (negInf);
header_ node_null.lft_node_addr = node_null;
header_node_null.rt_node_addr = node_null;
}
public boolean isEmpty ( )
{
return header_node.rt_node_addr = = node_null;
}
// we have to make the tree empty that too logically.
public void makeEmpty ( )
{
header_ node.rt_node_addr = = node_null;
}
public void insert (int obj)
{
curr_node = parent_node = grand_node = header_node;
node_null.node_info = obj;
while (curr_node.node_info ! = obj)
{
great_node = grand_node;
grand_node = parent_node;
parent_node = curr_node;
curr_node = obj < curr_node.node_data ? curr_node.lft_node_addr : curr_node.
// we have to check whether there are two children present or not.
If ( curr_node.lft_node_addr.color_of_node = = RED & & curr_node.rt_node_addr.colhandleReorient ( obj );
}
if (curr_node ! = node_null )
return;
curr_node = new node_RB_Tree (obj, node_null, node_null);
// we will now attach this to the parent node.
If (obj < parent_node.node_info)
Parent_node.lft_node_addr = curr_node;
Else
Parent_node.rt_node_addr = curr_node;
handleReorient ( obj );
}
Private void handleReorient ( int obj )
{
Curr_node.color_of_node = RED;
Curr_node.lft_node_addr.color_of_node = BLACK;
Curr_node.rt_node_addr.color_of_node = BLACK;
If ( parent_node.colr_of_node = = RED)
{
Grand_node.colr_of_node = RED;
If( obj < grand_node.node_data ! = obj < parent_node.node_data)
parent_node = rotate ( obj, grand_node );
curr_node = rotate ( obj, great_node );
curr_node.colr_of_node = BLACK;
}
header_node.rt_node_addr.colr_of_node = BLACK;
}
private node_RB_Tree rotate ( int obj, node_RB_Tree parent_node)
{
If (obj < parent_node.node_info)
Return parent_node.lft_node_addr = obj < parent_node.left_node_addr.node_info ? rotate
Else
Return parent_node.rt_node_addr = obj < parent_node.right_node_addr.node_info ?
}
private node_RB_Tree rotatewithlft_node_addrChild( Node_RB_Tree k2)
{
Node_RB_Tree k1 = k2.lft_node_addr;
k2.lft_node_addr = k1.rt_node_addr;
k1.rt_node_addr = k2;
Return k1;
}
private node_RB_Tree rotatewithright_node_addrChild( node_RB_Tree k1)
{
node_RB_Tree k2 = k1.rt_node_addr;
k1.rt_node_addr = k2.lft_node_addr;
k2.lft_node_addr = k1;
return k2;
}
public int countNodes()
{
return countNodes(header_node.right_node_addr);
}
private int countNodes(node_RB_Tree r)
{
if (r == node_null)
return 0;
else
{
int l = 1;
l += countNodes(r.lft_node_addr);
l += countNodes(r.rt_node_addr);
return l;
}
}
public boolean search(int val)
{
return search(header_node.rt_node_addr, val);
}
private boolean search(Node_RB_Tree r, int val)
{
boolean found = false;
while ((r != node_null) && !found)
{
int rval = r.node_data;
if (val < rval)
r = r.lft_node_addr;
else if (val > rval)
r = r.rt_node_addr;
else
{
found = true;
break;
}
found = search(r, val);
}
return found;
}
public void inorder()
{
inorder(header_node.rt_node_addr);
}
private void inorder(node_RB_Tree r)
{
if (r != node_null)
{
inorder(r.lft_node_addr);
char c = 'B';
if (r.colr_of_node == 0)
c = 'R';
System.out.print(r.node_data +""+c+" ");
inorder(r.rt_node_addr);
}
}
public void preorder()
{
preorder(header_node.rt_node_addr);
}
private void preorder(node_RB_Tree r)
{
if (r != node_null)
{
char c = 'B';
if (r.colr_of_node == 0)
c = 'R';
System.out.print(r.node_data +""+c+" ");
preorder(r.lft_node_addr);
preorder(r.rt_node_addr);
}
}
public void postorder()
{
postorder(header_node.rt_node_addr);
}
private void postorder(node_RB_Tree r)
{
if (r != node_null)
{
postorder(r.lft_node_addr);
postorder(r.rt_node_addr);
char c = 'B';
if (r.colour_of_node == 0)
c = 'R';
System.out.print(r.node_info +""+c+" ");
}
}
}
class RB_Tree_Run
{
public static void main(String[] arg)
{
Scanner scannner_obj = new Scanner(System.in);
RB_Tree_obj = new Red_Black_Tree(Integer.MIN_VALUE);
System.out.println("Red Black Tree Test\n");
char ch;
do
{
System.out.println("\nThe options list for Red Black Tree::\n");
System.out.println("1. To add a new node in the Red-Black Tree");
System.out.println("2. To search the Red-Black Tree for a node");
System.out.println("3. To get node count of nodes in Red Black Tree");
System.out.println("4. To check if the RB_Treeis Empty or not?");
System.out.println("5. To Clear the Red_Black_Tree.");
int option_list_choice = scannner_obj.nextInt();
switch (option_list_choice)
{
case 1 :
System.out.println("Enter integer node_data to insert");
red_black_tree_obj.insert( scannner_obj.nextInt() );
break;
case 2 :
System.out.println("Enter integer node_data to search");
System.out.println("Search result : "+ red_black_tree_obj.search( scannner_obj.nextInt() ));
break;
case 3 :
System.out.println("Nodes = "+ red_black_tree_obj.countNodes());
break;
case 4 :
System.out.println("Empty status = "+ red_black_tree_obj.isEmpty());
break;
case 5 :
System.out.println("\nTree Cleared");
red_black_tree_obj.makeEmpty();
break;
default :
System.out.println("Wrong Entry \n ");
break;
}
System.out.print("\nRBT in Post-order: ");
red_black_tree_obj.postorder();
System.out.print("\nRBT in Pre-order: ");
red_black_tree_obj.preorder();
System.out.print("\nRBT in In-order: ");
red_black_tree_obj.inorder();
System.out.println("\nWanna proceed further(Type y or n)? \n");
ch = scannner_obj.next().charAt(0);
} while (ch == 'Y'|| ch == 'y');
}
}
Output: