Threaded Binary Trees

Recursion or the usage of an auxiliary stack can both be used for in-order binary tree traversal. The goal of threaded binary trees is to speed up in-order traversal without using a stack or recursion. Making all right child pointers that would typically lead to NULL point to the node's inorder successor allows you to thread a binary tree (if it exists).

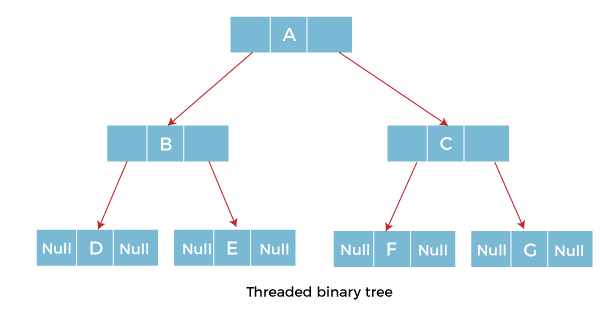
Threaded binary trees come in two different varieties.

1. Single-threaded: if successor exists.
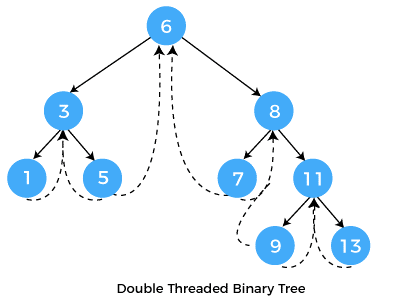
2. Double-threaded: When a process is double-threaded, its left and right NULL pointers are made to point, respectively, to its in-order predecessor and in-order successor. For postorder traversal and reverse inorder traversal, the predecessor threads are helpful.

The threads can also be used to access a node's ancestors quickly.

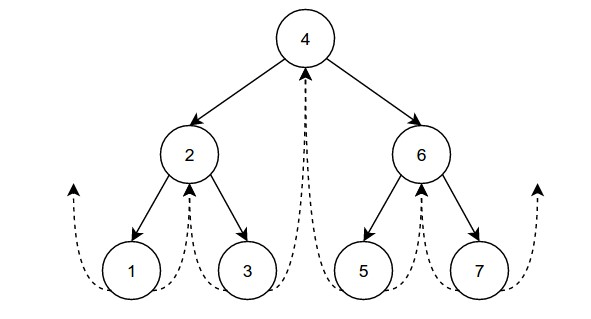
The single-threaded binary tree example is in the following diagram. The dotted lines depict threads.

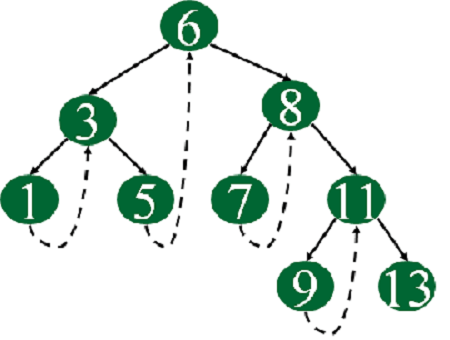
The boolean variable right thread is used to specify whether the right pointer points to the right child or the in-order successor since the right pointer serves two functions. We can add a left thread similarly for a binary tree with two threads.

Types of threaded binary trees.

The types of threaded Binary Trees are:

1. One-way Threaded Binary Tree.
2. Two-way Threaded Binary Tree.

One–way threaded binary Tree

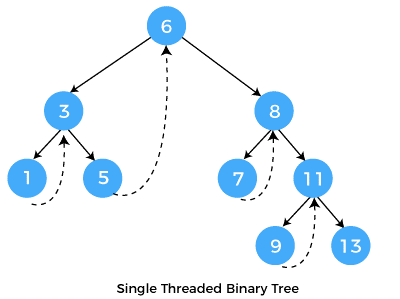
Right-threaded binary trees are these types of trees. A thread will point to the node's predecessor if it occurs in the left area of the node.

Additionally, a NULL value will be present for other nodes with values in the correct link field.

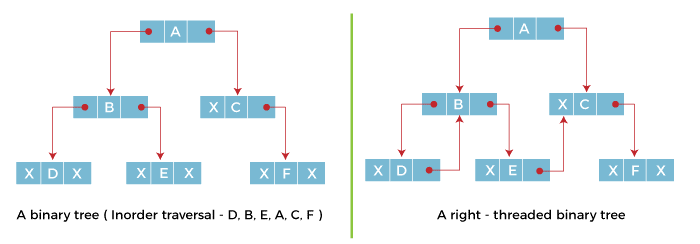
Two–way threaded binary tree

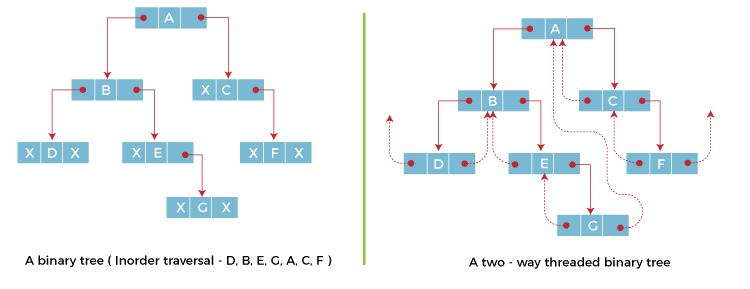
A, C, F, D, B, E, and G are the results of this binary Tree's inorder traversal, as seen in the above figure. Similarly, threads are used to replace node G's right and left linked fields such that the correct link field points to the node's inorder successor and the left link field point to the node's inorder predecessor. Other nodes with link fields with NULL values are similarly populated with threads.

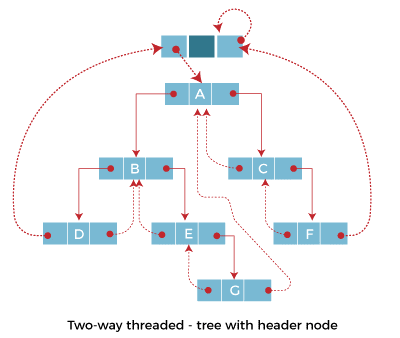
They lack an in-order predecessor and a successor, respectively, which explains this. Threads pointing in circles are a sign of this. Consequently, we keep a unique node known as the header node to preserve the uniformity of threads.

Operations in the threaded binary tree

A threaded binary tree can be used for three different types of operations:

1. Insert
2. Search
3. Delete

Let's take a closer look at each of these operations, where I'm utilizing a double-threaded binary tree:

Insertion in the threaded binary tree

1. The insert operation can add a new node to a threaded binary tree.

Case 1: In an empty threaded binary search tree, whenever a new node is added, its left and right pointers are set to null pointers. This process is the same for both binaries and threaded binary search trees.

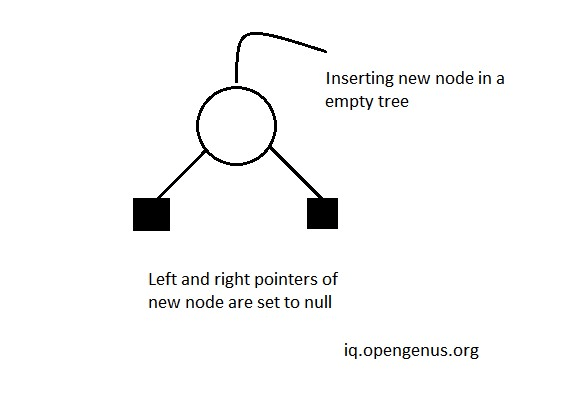
Case 2: When a new node is put into a binary search tree as a left child of an existing node, we conduct two operations on the parent node's struct and two operations on the child node's struct, for instance:

For the parent node, the right pointer now points to the newly added node, setting the parent's bool variable to true to indicate that a right child exists.

The complexity of time and space for insertion

O(logn) space complexity, O(log N) time complexity (1)

Search operation by a threaded binary tree

If search key < root, then.
   Go to the left thread.
else
   Go to the right thread.

We must repeat the process described above if we successfully find the required node.

It takes a while to look.

Time complexity gets an O (logn).

Deletion operation by a threaded binary tree

In the Threaded Binary Tree, delete

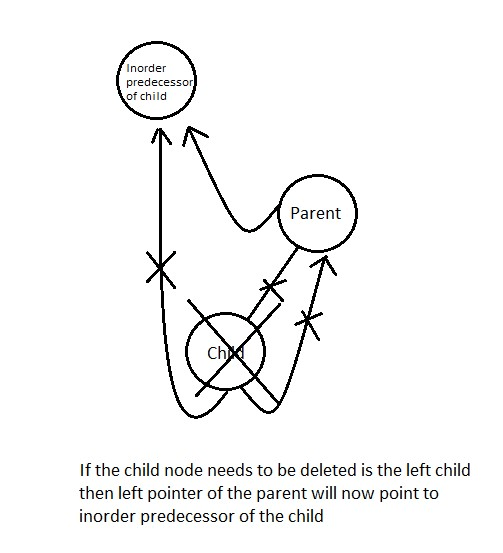
Case 1: In that case, the left thread of the parent node must be made to point to the left thread of the child after deletion, and the parent's leftThread must be set to false to indicate the parent is pointing to an out-of-order predecessor.

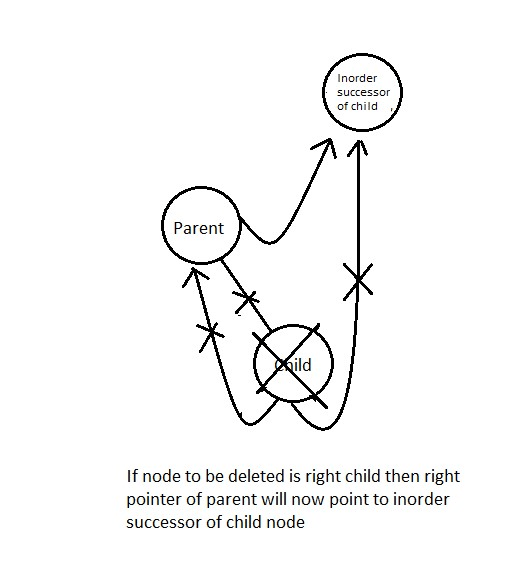
Similarly, if we delete the right child, the right thread is set to false, and the parent's right is made to point to the kid's right thread.

Advantages of threaded binary tree

1. This Tree's ability to traverse components linearly.
2. Because it uses linear traversal instead of stacks,
3. Allows for the automatic usage of the parent pointer when locating the parent node.
4. Nodes hold pointers to in-order predecessor and successor nodes, allowing for forward and backward traversal of nodes in an orderly way according to a threaded tree.