Stack Using Array
Stack – A Stack is a linear abstract data type used to store elements. It is also called last in first out or first in last out data structure because the newly added element is removed first from the stack and the element added first is removed in last.
The basic operations performed on the stack data structure are push and pop, where push operation is used to add elements at the top of the stack, and pop operation is used to remove the top element of the stack.
In array implementation of stack, the top pointer stores the index value of the latest element added to the stack, known as the top of the stack. It is also known as the static implementation of the stack because here we fix the size of the stack. During the run time it can never be increased.
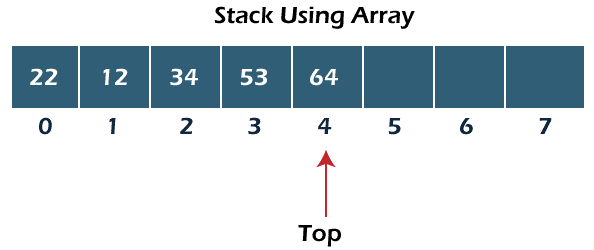
The value of the top pointer determines the condition of stack overflow and underflow. When the top pointer stores the maximum possible index value, we can clearly say that the stack is overflowing, and if it is negative, we can say that the stack is underflowing.
The C++ program to implement stack using array as the primitive data type is given below:
// Array implementation of stack in C++
#include <iostream>
using namespace std;
// Defining the stack of size 10
int stack[10];
int n = 10;
int top = -1;
// Push function to push element at the top of the element
void push(int value)
{
if (top == n - 1)
{
cout << "Stack overflow!" << endl;
}
else
{
top++;
stack[top] = value;
}
}
// Pop function to remove the top element from the stack
void pop()
{
if (top == -1)
{
cout << "Stack underflow!";
}
else
{
cout << "The popped element is " << stack[top] << endl;
top--;
}
}
// Function to search element in the stack
void search_in_stack(int value)
{
if (top == -1)
{
cout << "No element in stack" << endl;
}
for (int i = 0; i <= top; i++)
{
if (stack[i] == value)
{
cout << value << " is present in the stack!" << endl;
return;
}
}
cout << value << " is not present in the stack!" << endl;
}
// Function to display all the elements of the stack
void traverse()
{
if (top == -1)
{
cout << "No element in stack" << endl;
return;
}
cout << "Element of the stack are : ";
for (int i = 0; i <= top; i++)
{
cout << stack[i] << " ";
}
cout << endl;
}
// Driver function
int main()
{
cout << "Enter 1 to push element in the stack." << endl;
cout << "Enter 2 to pop element from the stack." << endl;
cout << "Enter 3 to search element in the stack." << endl;
cout << "Enter 4 to print all the element of the stack." << endl;
cout << "Enter 5 to exit from the program." << endl;
int choice, x;
do
{
cout << "Enter your choice : ";
cin >> choice;
switch (choice)
{
case 1:
cout << "Enter the value to push in the stack : ";
cin >> x;
push(x);
break;
case 2:
pop();
break;
case 3:
cout << "Enter the value to search in the stack : ";
cin >> x;
search_in_stack(x);
break;
case 4:
traverse();
break;
case 5:
cout << "Exited Successfully!";
break;
;
default:
cout << "Wrong choice!" << endl;
break;
}
} while (choice != 5);
return 0;
}
The sample output of the above program is given below:
Enter 1 to push anelement in the stack.
Enter 2 to pop an element from the stack.
Enter 3 to search an element in the stack.
Enter 4 to print all the elements of the stack.
Enter 5 to exit from the program.
Enter your choice : 1
Enter the value to push in the stack : 12
Enter your choice : 1
Enter the value to push in the stack : 34
Enter your choice : 1
Enter the value to push in the stack : 5
Enter your choice : 1
Enter the value to push in the stack : 67
Enter your choice : 1
Enter the value to push in the stack : 23
Enter your choice : 2
The popped element is 23
Enter your choice : 3
Enter the value to search in the stack : 45
45 is not present in the stack!
Enter your choice : 3
Enter the value to search in the stack : 23
23 is not present in the stack!
Enter your choice : 4
Element of the stack are : 12 34 5 67
Enter your choice : 5
Exited Successfully!
In the above program, the main function is programmed so that the program will be run according to the user’s choice. The stack operations or function calls will be done as per the user’s choice. Such types of programs are also known as menu-driven programs.
- POP operation – The POP operation is used to pop the top element of the stack, and the code of the same is explained below:
Here, we first check whether the stack is already empty or not, and the condition for the same is top = -1. If the stack is empty, we throw a warning that the stack is underflowing and no elements if present in the stack to pop. If the stack is not empty, we pop the top element by printing its value, and we decrement the value of the top pointer by 1, and the top pointer will store the index value of the very previous element. Here, we actually don’t delete the value from the stack or array, we forget the top element and make the very previous element as the top element of the stack.
void pop()
{
if (top == -1)
{
cout << "Stack underflow!";
}
else
{
cout << "The popped element is " << stack[top] << endl;
top--;
}
}
- PUSH Operation – The PUSH operation is used to add elements at the top of the stack, and the code of the push operation is explained below:
void push(int value)
{
if (top == n - 1)
{
cout << "Stack overflow!" << endl;
}
else
{
top++;
stack[top] = value;
}
}
To perform the push operation on a stack, we first check whether the stack is already full or not, and the condition for the same is top = n-1, where n is the size of the array. If the stack is already full, we can’t add an element to it, and we throw a warning of ‘stack overflow’. If the stack is not full, we first increment the value of the top pointer by 1 and add the new element at the top index. The newly added element becomes the new top element of the stack.
- Searching is stack – One cannot easily search for an element in a stack. As the basic operations performed on a stack are push and pop. The code for the search element in a stack is explained below:
void search_in_stack(int value)
{
if (top == -1)
{
cout << "No element in stack" << endl;
}
for (int i = 0; i <= top; i++)
{
if (stack[i] == value)
{
cout << value << " is present in the stack!" << endl;
return;
}
}
cout << value << " is not present in the stack!" << endl;
}
We are using the linear search here, as we have implemented our stack using an array. We are traversing the stack from the 0th index to the top index. We match the input value one by one, and if we find the element, we give the output as “the element is present in the stack”. If not, we give the output as “the element is not present”. Before searching for the element, we first check the stack underflow condition.
- Stack Traversal – There are two methods to traverse a stack. In the first method, we pop all the stack elements. In the second method, we traverse the stack internally depending on which primitive data structure is used to implement that stack without popping any element from it. The code of stack traversal is explained below:
void traverse()
{
if (top == -1)
{
cout << "No element in stack" << endl;
return;
}
cout << "Element of the stack are : ";
for (int i = 0; i <= top; i++)
{
cout << stack[i] << " ";
}
cout << endl;
}
Here, we are internally traversing all the elements starting from the 0th index to the top index and printing all the values as the program’s output without removing any element from the stack. Before traversing the stack, we have checked the condition of stack underflow.