Bubble Sort vs Selection Sort

In this article, we will discuss the basic differences between these two sorting algorithms. Let us have a quick overview of what these sorting algorithms are? And what are the ideas behind them?

What is Bubble Sort? and discuss the idea using an example.

Bubble Sort – The idea behind the bubble sort is to compare two adjacent elements of an array and swap them if the predecessor is greater than the successor. On each iteration, it maintains the order between two adjacent elements means a smaller value should come before a larger value. The pseudo-code of the bubble sort is given below:

Bubble_Sort (int a[], int n)
{
	for i =1 to n-1
	{
		for j = 0 to n - i – 1
		{
			If a[j] > a[j + 1]
				swap (a[j], a[j + 1])
		}
	}
} // Where n is the size of the array

The first for-loop starts from 1 and ends at n -1, and the second for-loop starts from 0 and ends at n - i – 1. After each complete iteration of the external for loop, the size of the sorted array is increased by one, and the size of the unsorted array is decreased by 1.

Now let us see how it works through an example.

Consider an unsorted array of 6 elements, let’s say a[] = {24, 12, 3, 6, 11, 9}. Now, we will sort the above array using the Bubble Sort.

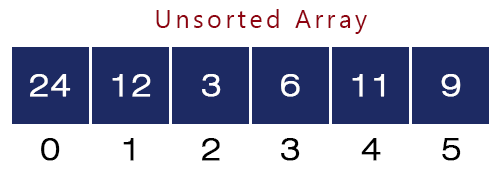
• First Iteration – i = 1 j = 0 to 6 - 1 – 1 = 4
  • j = 0. Here, a[0] = 24 and a[1] = 12 and 24 > 12, we swap these two values and the array be will like as shown in the figure below:

• j = 1. Here, a[1] = 24 and a[2] = 3 and 24 > 3, we swap these two values, and the array be will like as shown in the figure below:

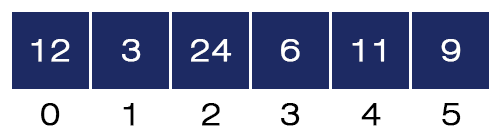
• j = 2. Here, a[2] = 24 and a[3] = 6 and 24 > 6, we swap these two values, and the array will be like as shown in the figure below:

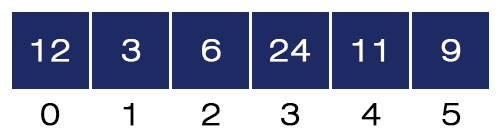
• j = 3. Here, a[3] = 24 and a[4] = 11 and 24 > 11, we swap these two values, and the array will be like as shown in the figure below:

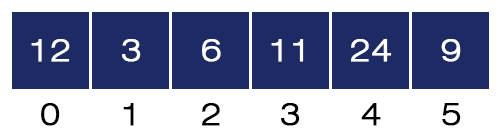
• j = 4. Here, a[4] = 24 and a[5] = 9 and 24 > 9, we swap these two values, and the array will be like as shown in the figure below:

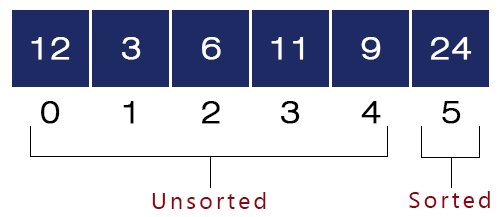
• Second Iteration – i = 2, j = 0 to 6 – 2 – 1 = 3
  • j = 0. Here, a[0] = 12 and a[1] = 3 and 12 > 3, we swap these two values and the array will be like as shown in the figure below:

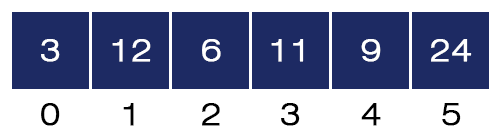
• j = 1. Here, a[1] = 12 and a[2] = 6 and 12 > 6, we swap these two values, and the array will be like as shown in the figure below:

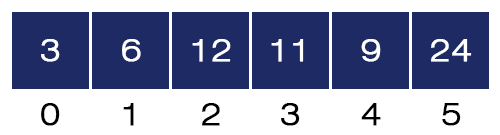
• j = 2. Here, a[2] = 12 and a[3] = 11 and 12 > 11, we swap these two values, and the array will be like as shown in the figure below:

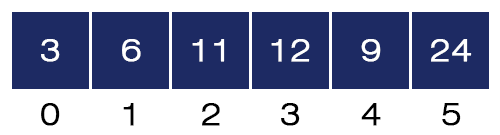
• j = 3. Here, a[3] = 12 and a[4] = 9 and 12 > 9, we swap these two values and the array will be like as shown in the figure below:

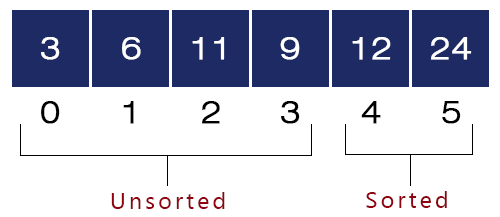
• Third Iteration – i = 3, j = 0 to 2
  • j = 0. Here, a[0] = 3 and a[1] = 3 and 3 < 6, we won’t swap them and the array will be like as shown in the figure:

• j = 1. Here, a[1] = 6 and a[2] = 11 and 6 < 11, we won’t swap them and the array will be like as shown in the figure:

• j = 2. Here, a[2] = 11 and a[3] = 9 and 11 > 9, we swap these two values, and the array will be like as shown in the figure below:

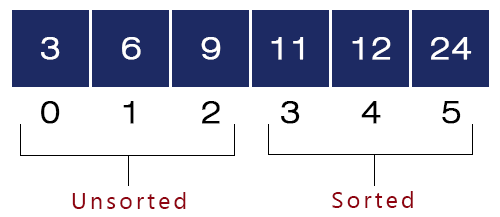
• Fourth Iteration – i = 4, j = 0 to 1
  • j = 0. a[0] = 3 and a[1] = 6 and 3 < 6, we won’t swap them and the array will be like as shown in the figure:

• j = 1. a[1] = 6 and a[2] = 9 and 6 < 9, we won’t swap them and the array will be like as shown in the figure:

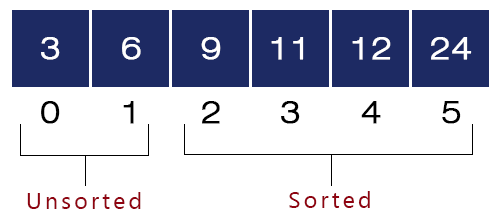
• Fifth Iteration – i = 5, j = 0 to 0
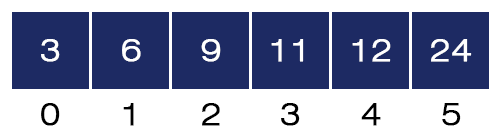
  • j = 1. a[0] = 3 and a[1] = 6 and 3 < 6, we won’t swap them and the array will be like as shown in the figure:

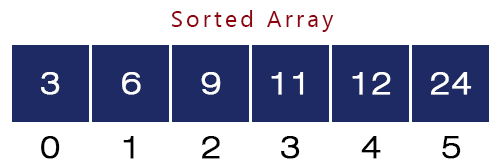
After completing the 5^th iteration, we get our sorted array.

What is Selection Sort?

Selection sort – The idea is to find the array’s minimum element and place it at its correct position. In this sorting technique, we divide the given array into two sorted and unsorted subarrays. Initially, we assume the size of the sorted array is zero, and the size of the unsorted array is the size of the array itself. On each iteration, we find the unsorted array’s minimum element, swap it with its first element, and increase the size of the sorted array by one.

The pseudo-code of the Selection sort function is given below:

Selection Sort (int a[], int n) 
{
    For i = 0 to n - 2 
    {
        Min_index = i; 
        For j = i+1 to n - 1 
        {
            If (a[j] < a[Min_index]) 
                Min_index = j;
        }
        If i != min_index
       	      swap(a[i], a[Min_index]); 
    }
} // Where Min_index is the index of the minimum element and n is the size of the array.

The first for loop starts from 0 and ends at n – 2, and the second for loop starts from i + 1 and ends at n – 1. After each complete execution of the internal for loop, the unsorted array’s minimum element is placed at its correct position in the sorted array.

Let us understand this through an example. We take an unsorted array a[] = {24, 12, 3, 6, 11, 9} of size = 6.

• First iteration – i = 0, j = 1 to 6 – 1 = 5, min_index = i = 0
  • J = 1, a [j = 1] = 12 and a[min_index = 0] = 24 and 12 < 24. If condition is satisfied, we update the min_index = j = 1.
    
  • J = 2, a[ j = 2] = 3 and a[min_index = 1] = 3 and 3 < 12. If condition is satisfied, we update the min_index = j = 2.
  • J = 3, a[ j = 3] = 6 and a[min_index = 2] = 3 and 6 > 3. If condition is not statisfied.
  • J = 4, a[ j = 4] = 11 and a[min_index = 2] = 3 and 11 > 3. If condition is not statisfied.
    
  • J = 5, a[ j = 5] = 9 and a[min_index = 2] = 3 and 9 > 3. If condition is not statisfied.

We swap a[i = 0] = 24 and a[min_index = 2] = 3. Now, the array will look like as shown in the figure.

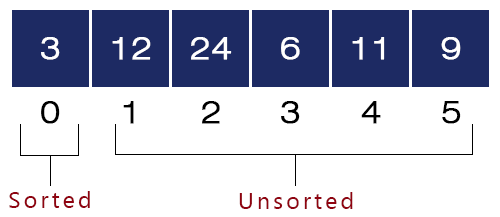
• Second Iteration – i = 1, j = 2 to 5, min_index = i = 1
  • J = 2, a[ j = 2] = 24 and a[min_index = 1] = 12 and 12 < 24. If condition is not statisfied.
    
  • J = 3, a[ j = 3] = 6 and a[min_index = 1] = 12 and 6 < 12. If condition is satisfied, we update the min_index = j = 3.
    
  • J = 4, a[ j = 4] = 11 and a[min_index = 3] = 6 and 11 > 6. If condition is not statisfied.
    
  • J = 5, a[ j = 5] = 9 and a[min_index = 3] = 6 and 9 > 6. If condition is not statisfied.

We swap a[i = 1] = 12 and a[min_index = 3] = 6. Now, the array will look like as shown in the figure.

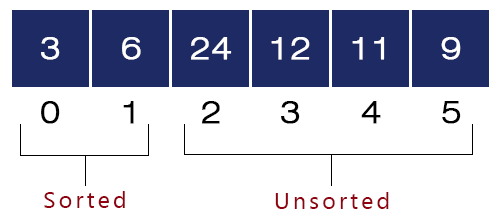
• Third Iteation – i  = 2, j = 3 to 5, min_index = i = 2
  • J = 3, a[ j = 3] = 12 and a[min_index = 2] = 24 and 12 < 24. If condition is satisfied, we update the min_index = j = 3.
    
  • J = 4, a[j = 4] = 11 and a[min_index = 3] = 12 and 11 < 12. If condition is satisfied, we update the min_index = j = 4.
    
  • J = 5, a[j = 5] = 9 and a[min_index = 4] = 11 and 9 < 11. If condition is satisfied, we update the min_index = j = 5.

We swap a[i = 2] = 24 and a[min_index = 5] = 9. Now, the array will look like as shown in the figure.

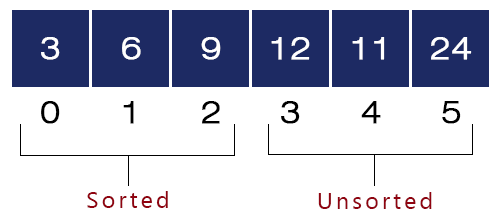
• Fourth Iteration – i = 3, j = 4 to 5, min_index = i = 3
  • J = 4, a[j = 4] = 11 and a[min_index = 3] = 12 and 11 < 12. If condition is satisfied, we update the min_index = j = 4.
    
  • J = 5, a[ j = 5] = 24 and a[min_index = 4] = 11 and 24 > 11. If condition is not statisfied.

We swap a[i = 3] = 12 and a[min_index = 4] = 11. Now, the array will look like as shown in the figure.

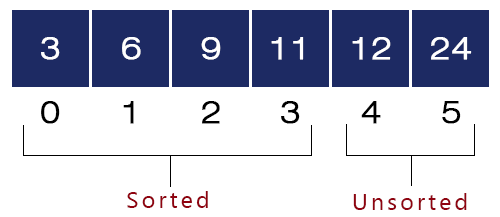
• Fifth Iteration – i = 4, j = 5 to 5, min_index = i = 4
  • J = 5, a[ j = 5] = 24 and a[min_index = 4] = 12 and 24 > 12. If condition is not satisfied.

Here, i is equal to min_index, no swapping occurs, and after completing the fifth iteration, we get our sorted array.

Differences between Bubble Sort and Selection Sort:

The main differences between these two sorting techniques are listed below in the table:

	Bubble Sort	Selection Sort
Idea or Approach	The idea is to compare two adjacent elements in the unsorted array and place them in increasing or decreasing order.	The idea is to find the smallest element in the unsorted array and place it in its correct position.
Time Complexity	Best case: T(n) = O(n) Average case: T(n) = O(n^2) Worst case: T(n) = O(n^2)	Best case: T(n) = O(n^2) Average case: T(n) = O(n^2) Worst case: T(n) = O(n^2)
Space Complexity	Worst case: T(n) = O(1)	Worst case: T(n) = O(1)
Efficiency	Less efficient compared to Selection Sort	More efficient compared to Bubble Sort
Speed	Slower than selection sort as many comparisons and swapping are required.	Much faster than the bubble sort, a smaller number of comparisons and swapping are required.
Stability	Stable – The order of the elements remains preserved.	Unstable – The order of the elements doesn’t remain preserved.
Method	The comparison method is used to sort an array.	The selection method is used to sort an array.