Data Structures Tutorial

Data Structures Tutorial Asymptotic Notation Structure and Union Array Data Structure Linked list Data Structure Type of Linked list Advantages and Disadvantages of linked list Queue Data Structure Implementation of Queue Stack Data Structure Implementation of Stack Sorting Insertion sort Quick sort Selection sort Heap sort Merge sort Bucket sort Count sort Radix sort Shell sort Tree Traversal of the binary tree Binary search tree Graph Spanning tree Linear Search Binary Search Hashing Collision Resolution Techniques

Misc Topic:

Priority Queue in Data Structure Deque in Data Structure Difference Between Linear And Non Linear Data Structures Queue Operations In Data Structure About Data Structures Data Structures Algorithms Types of Data Structures Big O Notations Introduction to Arrays Introduction to 1D-Arrays Operations on 1D-Arrays Introduction to 2D-Arrays Operations on 2D-Arrays Strings in Data Structures String Operations Application of 2D array Bubble Sort Insertion Sort Sorting Algorithms What is DFS Algorithm What Is Graph Data Structure What is the difference between Tree and Graph What is the difference between DFS and BFS Bucket Sort Dijkstra’s vs Bellman-Ford Algorithm Linear Queue Data Structure in C Stack Using Array Stack Using Linked List Recursion in Fibonacci Stack vs Array What is Skewed Binary Tree Primitive Data Structure in C Dynamic memory allocation of structure in C Application of Stack in Data Structures Binary Tree in Data Structures Heap Data Structure Recursion - Factorial and Fibonacci What is B tree what is B+ tree Huffman tree in Data Structures Insertion Sort vs Bubble Sort Adding one to the number represented an array of digits Bitwise Operators and their Important Tricks Blowfish algorithm Bubble Sort vs Selection Sort Hashing and its Applications Heap Sort vs Merge Sort Insertion Sort vs Selection Sort Merge Conflicts and ways to handle them Difference between Stack and Queue AVL tree in data structure c++ Bubble sort algorithm using Javascript Buffer overflow attack with examples Find out the area between two concentric circles Lowest common ancestor in a binary search tree Number of visible boxes putting one inside another Program to calculate the area of the circumcircle of an equilateral triangle Red-black Tree in Data Structures Strictly binary tree in Data Structures 2-3 Trees and Basic Operations on them Asynchronous advantage actor-critic (A3C) Algorithm Bubble Sort vs Heap Sort Digital Search Tree in Data Structures Minimum Spanning Tree Permutation Sort or Bogo Sort Quick Sort vs Merge Sort Boruvkas algorithm Bubble Sort vs Quick Sort Common Operations on various Data Structures Detect and Remove Loop in a Linked List How to Start Learning DSA Print kth least significant bit number Why is Binary Heap Preferred over BST for Priority Queue Bin Packing Problem Binary Tree Inorder Traversal Burning binary tree Equal Sum What is a Threaded Binary Tree? What is a full Binary Tree? Bubble Sort vs Merge Sort B+ Tree Program in Q language Deletion Operation from A B Tree Deletion Operation of the binary search tree in C++ language Does Overloading Work with Inheritance Balanced Binary Tree Binary tree deletion Binary tree insertion Cocktail Sort Comb Sort FIFO approach Operations of B Tree in C++ Language Recaman’s Sequence Tim Sort Understanding Data Processing Applications of trees in data structures Binary Tree Implementation Using Arrays Convert a Binary Tree into a Binary Search Tree Create a binary search tree Horizontal and Vertical Scaling Invert binary tree LCA of binary tree Linked List Representation of Binary Tree Optimal binary search tree in DSA Serialize and Deserialize a Binary Tree Tree terminology in Data structures Vertical Order Traversal of Binary Tree What is a Height-Balanced Tree in Data Structure Convert binary tree to a doubly linked list Fundamental of Algorithms Introduction and Implementation of Bloom Filter Optimal binary search tree using dynamic programming Right side view of binary tree Symmetric binary tree Trim a binary search tree What is a Sparse Matrix in Data Structure What is a Tree in Terms of a Graph What is the Use of Segment Trees in Data Structure What Should We Learn First Trees or Graphs in Data Structures All About Minimum Cost Spanning Trees in Data Structure Convert Binary Tree into a Threaded Binary Tree Difference between Structured and Object-Oriented Analysis FLEX (Fast Lexical Analyzer Generator) Object-Oriented Analysis and Design Sum of Nodes in a Binary Tree What are the types of Trees in Data Structure What is a 2-3 Tree in Data Structure What is a Spanning Tree in Data Structure What is an AVL Tree in Data Structure Given a Binary Tree, Check if it's balanced B Tree in Data Structure Convert Sorted List to Binary Search Tree Flattening a Linked List Given a Perfect Binary Tree, Reverse Alternate Levels Left View of Binary Tree What are Forest Trees in Data Structure Compare Balanced Binary Tree and Complete Binary Tree Diameter of a Binary Tree Given a Binary Tree Check the Zig Zag Traversal Given a Binary Tree Print the Shortest Path Given a Binary Tree Return All Root To Leaf Paths Given a Binary Tree Swap Nodes at K Height Given a Binary Tree Find Its Minimum Depth Given a Binary Tree Print the Pre Order Traversal in Recursive Given a Generate all Structurally Unique Binary Search Trees Perfect Binary Tree Threaded Binary Trees Function to Create a Copy of Binary Search Tree Function to Delete a Leaf Node from a Binary Tree Function to Insert a Node in a Binary Search Tree Given Two Binary Trees, Check if it is Symmetric A Full Binary Tree with n Nodes Applications of Different Linked Lists in Data Structure B+ Tree in Data Structure Construction of B tree in Data Structure Difference between B-tree and Binary Tree Finding Rank in a Binary Search Tree Finding the Maximum Element in a Binary Tree Finding the Minimum and Maximum Value of a Binary Tree Finding the Sum of All Paths in a Binary Tree Time Complexity of Selection Sort in Data Structure How to get Better in Data Structures and Algorithms Binary Tree Leaf Nodes Classification of Data Structure Difference between Static and Dynamic Data Structure Find the Union and Intersection of the Binary Search Tree Find the Vertical Next in a Binary Tree Finding a Deadlock in a Binary Search Tree Finding all Node of k Distance in a Binary Tree Finding Diagonal Sum in a Binary Tree Finding Diagonal Traversal of The Binary Tree Finding In-Order Successor Binary Tree Finding the gcd of Each Sibling of the Binary Tree Greedy Algorithm in Data Structure How to Calculate Space Complexity in Data Structure How to find missing numbers in an Array Kth Ancestor Node of Binary Tree Minimum Depth Binary Tree Mirror Binary Tree in Data Structure Red-Black Tree Insertion Binary Tree to Mirror Image in Data Structure Calculating the Height of a Binary Search Tree in Data Structure Characteristics of Binary Tree in Data Structure Create a Complete Binary Tree from its Linked List Field in Tree Data Structure Find a Specified Element in a binary Search Tree Find Descendant in Tree Data Structure Find Siblings in a Binary Tree Given as an Array Find the Height of a Node in a Binary Tree Find the Second-Largest Element in a Binary Tree Find the Successor Predecessor of a Binary Search Tree Forest of a Tree in Data Structure In Order Traversal of Threaded Binary Tree Introduction to Huffman Coding Limitations of a Binary Search Tree Link State Routing Algorithm in Data Structure Map Reduce Algorithm for Binary Search Tree in Data Structure Non-Binary Tree in Data Structure Quadratic Probing Example in Hashing Scope and Lifetime of Variables in Data Structure Separate Chaining in Data Structure What is Dynamic Data Structure Separate Chaining vs Open Addressing Time and Space Complexity of Linear Data Structures Abstract Data Types in Data Structures Binary Tree to Single Linked List Count the Number of Nodes in the Binary Tree Count Total No. of Ancestors in a Binary Search Tree Elements of Dynamic Programming in Data Structures Find cost of tree with prims algorithm in data structures Find Preorder Successor in a Threaded Binary Tree Find Prime Nodes Sum Count in Non-Binary Tree Find the Right Sibling of a Binary Tree with Parent Pointers Find the Width of the Binary Search Tree Forest trees in Data Structures Free Tree in Data Structures Frequently asked questions in Tree Data Structures Infix, Postfix and Prefix Conversion Time Complexity of Fibonacci Series What is Weighted Graph in Data Structure What is the Advantage of Linear Search?

Applications of trees in data structures
2022-10-23 03:33:00

Applications of trees in data structures

Data structures

Storage used to organize and store data is known as the data structure. It is a method of managing computerized data to translate or retrieve it more efficiently. A data structure is a database used to store and manage data and optimize and manage computing resources.

Data structures are not just for storing data. It is also used for processing, storage, and preservation. Almost every program or application contains basic and advanced data structures. We have many simple and advanced data structures, and finding a program in a programming language that does not have a data structure is complicated.

A data structure is a form used intelligently and quickly, storing, processing, organizing, and storing data in a machine or computer format. Data structures help represent data for ease of use and manipulation. Every basic program, software, or application consists of two components: data and algorithm - data communication and algorithmic rules and regulations.

We can depict all the above in the following two simple equations:

Operations that are permissible on the data + Related data = Data Structure

Algorithms + Data structures = Programs

There are two types of data structures

  • Linear Data structures
  • Non-linear data structures

Linear Data structures

In linear data structures, each element is related and followed by a component. So you can delete the instance. There are four types of this data structure. They are:

  • Linked lists
  • Queue
  • Array
  • Stack

Non-linear Data structures

In Non-linear data structures, content is not a series of information presented at different levels. There are several ways to pass from one element to another indirectly. Unauthorized data points are shared at least once. There are two types of this non-linear data structure. They are:

  • Tree data structure
  • Graph data structure

Tree Data structure

A tree is a hierarchical, non-linear file with nodes. Each tree section contains a table of values and store names that refer to other units ("Children"). This document editor is a great way to organize your content and quickly transfer it to your computer. A tree data structure consists of child, structure, and root nodes associated with fields, and this data also contains leaves, branches, and related roots.

The data in the Tree is non-linear. But it is organized differently, more precisely, hierarchically. Trees are considered non-linear because they are hierarchical. Tree data is organized into columns, groups, arrays, and linked lists. A tree is a hierarchical structure; A data model consists of nodes representing and supporting processes. Asynchronous data stores store different data types in a tree-like data structure called a root. All kinds of data are stored in a central location. Each line contains a message. The branches at the bottom of the Tree are called data models.

A type of binary Tree. This is for security purposes only and is a private message. Since this data structure is a separate tree, it can have at most two children. A binary tree can always have 0, 1, or 2 children. This allows a binary tree to provide the benefits of a linked list and an array, making it easier to find hidden objects (since they are mutable data structures). A binary search tree can traverse a nested list and match its speed.

The Tree data structures have different parts. They are:

  1. Degree of the node
  2. Height of the tree
  3. Internal nodes
  4. Leaf nodes
  5. Root node
  6. Edge
  7. Child node
  8. Siblings

Basic terminology used in the Tree Data structures:

Before understanding any concept, we must be familiar with the language usually used in the topic. Hence, below are the basic terminology traditionally used in the tree data structure concept.

  • Node – The entities in a tree data structure are called nodes, and a node is a place where we store our data or information.
  • Edge - An edge is a connection between any two nodes in a tree data structure, and the nodes and edges together make a tree data structure.
  • Root node – The root node only has child nodes, and it does not have any parent nodes. We can also say that the node that does not have a parent node in a tree data structure is the root node.
  • Parent node – The node that is a predecessor of a particular node is treated as its parent node. Any node in a tree data structure can have only one parent node.
  • Child node – The node that is a successor of a particular node is treated as its child node. (In a binary tree, each node can only have a maximum of 2 child nodes).
  • External node or Leaf node – The nodes that do not precede any other node (have no child nodes) are called external nodes or leaf nodes. (Dead end of any branch in the tree data structure is called an external node or leaf node in layman's terms).
  • Ancestor of a node – Let us consider a particular node as 'n' from a tree data structure. Any node that comes in the path while traversing from the root node to 'n' is the ancestor of the node 'n', including the root node.
  • Descendant - Let us consider a particular node as 'n' from a tree data structure. Any node that comes in the path while traversing from 'n' to any leaf node is the descendant of the node 'n', including the leaf nodes.
  • Sibling – Child nodes of a particular node are known as siblings.
  • Neighbour of a node – Both parents and children of a particular node are treated as the neighbours of that node.
  • Internal node – All the nodes except the root node and leaf nodes are treated as internal nodes.
  • Subtree – Any node under the root node, along with its chosen descendants, is known as a subtree.

For example,

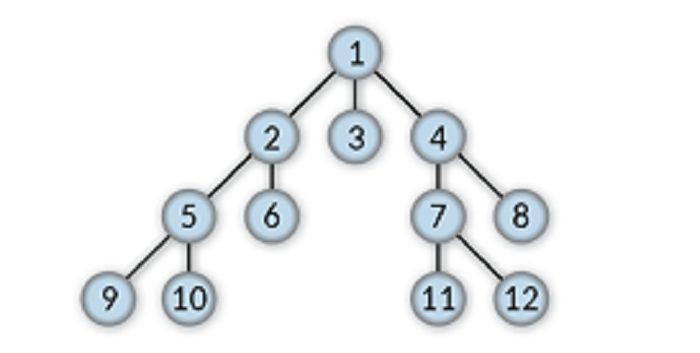
Applications of trees in data structures

The image mentioned above represents a tree data structure.

  • 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, and 12 are the Tree nodes.
  • The lines connecting each node represent edges.
  • '1' is the root node in this example.
  • '1' is also the parent node for 2, 3, and 4.
  • '2' is the parent node for 5 and 6
  • 7 and 8 are the child nodes of 4.
  • 9, 10, 6, 3, 11, 12, and 8 are called external nodes or root nodes.
  • 5, 2, and 1 are the ancestor nodes of 9.
  • 7, 8, 11, and 12 are the descendants of 4.
  • 2, 3, and 4 are the sibling nodes as they all have a common parent node (1).
  • 6, 1, and 5 are the neighbour nodes of 2.
  • The level of node 7 is equal to two (2).
  • 2, 4, 5, and 7 are the internal nodes.

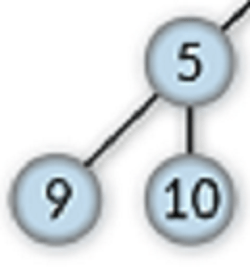
An example of a sub-tree derived from the above Tree is

Applications of trees in data structures

Properties of a tree

  • The number of edges – The connection between two nodes in a tree data structure is known as an edge. If the total number of nodes in a tree data structure is equal to 'n', then the number of advantages in that data structure is equivalent to 'n-1'. There can be only a single path between any two nodes in a tree data structure.
  • Degree of a node – The count of a total number of subtrees that can be extracted from a chosen node of a tree data structure is known as the degree of that node. The degree of any leaf node in a tree data structure must be zero (0). The degree of the root node (also called the degree of the Tree) must have the maximum degree compared to any other nodes in the tree data structure.
  • Degree of the Tree – The degree of the root node is treated as the degree of the Tree.

 Applications of trees

There are many applications of trees in data structures, and some are listed below:

  • Keys can be organized as a tree (like in a BST (Binary search tree)). This helps search any given tree easier and quicker than Linked Lists. However, it is slower compared to arrays. Red-black trees and AVL (Adelson, Velskii & Landis Tree) are self-balancing search trees that guarantee an upper bound of O(log N) for search.
  • Keys can be deleted or inserted in a reasonable time, which means we can delete or insert any given tree more easily and quickly than on Linked Lists. However, it is slower compared to arrays. Red-black trees and AVL (Adelson, Velskii & Landis Tree) are self-balancing search trees that guarantee an upper bound of O(log N) for deletion or insertion.
  • The implementation of pointers in the tree data structure is similar to linked lists but differs from arrays. This means that the nodes are linked using pointers and do not have an upper limit.
  • The tree data structure stores data in an organization structure, like folder structure (HTML, XML, etc.). This data structure stores hierarchical data.
  • A binary Search Tree (BST) is a particular type of tree data structure. It is helpful in quick insertion, deletion, and searching for sorted data. You can also find the closest item in the Binary search tree (BST).
  • Heap is another type of Tree, and they are used for priority queue implementations and array implementations.
  • B+ Tree and B Tree are used for implementing the indexing in databases.
  • The Syntax tree is used for parsing, scanning code generation, and evaluating an arithmetic expression in Compiler design.
  • K-D tree is another type of tree data structure, and it is used as a space partitioning tree. This tree data structure organizes points in K-dimensional space.
  • A tree is an example of the tree data structure that implements dictionaries with prefix lookup.
  • A quick pattern search can be done in a fixed text by a Suffix tree.
  • The bridges and routers used in computer networks take the help of the shortest path tree and spanning Tree to perform.
  • The tree data structures are used as workflows and composite virtual images for visual effects.
  • The tree data structure is used as a Decision tree.
  • Tree data structures are used as organization charts for large companies.
  • They are used in parsing XML files.
  • Tree data structures are used in writing algorithms for machine learning models.
  • They are used in many servers - for example, Domain Name Server (DNS), etc.
  • Tree data structures are used in building computer graphics.
  • They are used in the evaluation of expressions.
  • The tree data structure stores the defense moves of a player in virtual board games.
  • They are used in Java virtual machines (JVM).