All About Minimum Cost Spanning Trees in Data Structure

Data management is called database management. This allows the computer to sort or organize the data for efficient retrieval. A data model is a system that stores, manages, and optimizes computer resources. Data processing is not just about data storage. Almost every app or program has notices and updates about its version. Data structures are so simple and complex that it is difficult to program with a programming language that does not have data structures.

Data processing is the process of using intelligence and software to manage, organize, store and store information on a computer device or system. Data models provide visualization for easy data organization and management. Any basic process, program, or program has two parts: data and algorithms - the rules and regulations of data exchange and algorithms.

There are two types of data structures:

1. Linear Data structures
2. Non-linear data structures

Linear Data structures

This data type adds data to the data type. It's all about the process. You can then delete the duplicate. There are four types of linear data, they are:

1. Queue
2. Stack
3. Linked lists
4. Array

Non-linear Data structures

Data formats can be created in a variety of ways. There are two types of interpersonal communication:

1. Tree data structure
2. Graph data structure

Tree Data structure

The information about the tree is self-explanatory. Trees are ordered and, therefore, not linear. But they are designed differently.

Tree A node-based data model that represents and supports the structure as a structure. In an asynchronous database, data is stored in a tree data structure called a database. All data types are stored in a central location. Each line of text is called the lower branch of the data type tree.

Two types of plants. This is limited to confidential information. Because this data processing is an individual process, there can be more than two children. This means that a binary plant can produce 0, 1, or 2 seeds at any time. Binary search trees can quickly parse nested and linked expressions. This allows binary trees to provide values ??from list and associate arrays. This makes it easier to find hidden items. (Because it is a powerful data structure)

Graph data structure

In a simple sentence, we can say that graph- is a set of vertices (V) and edges (E) which is denoted as G (V, E). The graph has two sets, considered V and E. These vertices are also called nodes, and edges are referred to as arcs connecting any two nodes in a graph. These are usually accustomed to solving several real-time problems efficiently. These represent networks like a city's telephones, circuitry, and paths. These are also used on many social platforms like Facebook, LinkedIn, etc. Let us consider an example of each user or person on Facebook as a vertex (or node) in the graph. Each vertex has information about the user, like name, gender, etc., and the connection between each node or vertex is considered an edge or arc.

These are also used in the operating system as resource location graphs. These are also used in Google maps to find the shortest distance between two places, these are also used in airlines to know the best effective route, used in transportation, in circuits it is used to represent the nodes or circuitry points, these are used to solve challenging puzzles like mazes, these are also used in computer networking, there are many advantages of using graphs like it is straightforward to work with the algorithms like DFS and BFS, it has many practical applications, because of its nature(non-linear data structure) it is used in solving many complex problems, it helps in understanding and visualizing complex issues.

Spanning tree

The subsets of graphs where all the vertices of the graphs are covered with a minimum number of possible edges are called spanning trees. Therefore, we can conclude that a spanning tree can have no cycles nor can be disconnected between any two vertices of the graph (It must be a connected graph)

Based on the definition of a spanning tree, we can observe that all the uni-directed and connected graphs have at least one spanning tree. A disconnected graph has no spanning tree, as a path cannot be formed between the two disconnected vertices.

Therefore, it can be concluded that a single connected graph can possess more than one spanning tree; spanning trees are subsets of the original graph, and disconnected graphs can never possess a spanning tree.

Properties of spanning trees

1. A single connected graph can possess more than one spanning tree.
2. The number of edges of all the spanning trees formed from a single graph G is equal.
3. Spanning trees are acyclic, i.e., they do not contain any loops.
4. We depict a spanning tree as minimally connected, i.e., if an edge is removed between any two vertices of a spanning tree, it becomes disconnected.
5. If a spanning tree has N number of vertices, then its number of edges is given by (n – 1)
6. A spanning tree can be constructed by removing a maximum number of e – n + 1 edges from a given graph G.
7. A maximum of n^{n – 2} number of spanning trees can be formed for a given complete graph.

Cost of a spanning tree

In a weighted tree, the sum of the weights of its edges is known as the cost of the spanning tree.

Note

Weighted tree

The trees whose edges are allotted by weights are known as weighted trees.

Minimum cost spanning tree

As any tree can have many numbers of spanning trees, the spanning tree whose cost is the least compared to all the other spanning trees of a given tree is treated as a minimum-cost spanning tree. We can also have more than one minimum cost spanning tree for a given tree (but the cost of all these minimum costs spanning trees (of a single tree) must be the same). The minimum cost spanning tree of a given tree can be drawn with the help of two popular algorithms. The algorithms are named: Kruskal's algorithm and Prim's algorithm.

Application of minimum cost spanning trees

The applications of the minimum cost spanning trees can be found in the design of networks. For example, the minimum cost spanning trees algorithm can be applied to solve the problems like,

1. minimum cost weight perfect matching
2. multi-terminal minimum cut problem
3. approximating the traveling salesman problem
4. image segmentation
5. handwriting recognition
6. cluster analysis

Example:

Let us see the minimum cost spanning tree of the tree below:

An example of the minimum cost spanning tree is

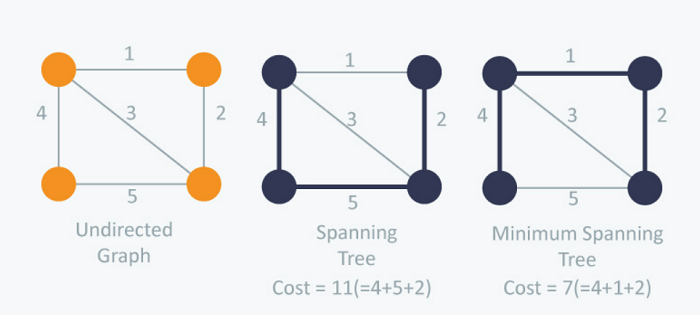
We can observe that the given tree has a minimum cost spanning tree of cost 7

Algorithms to determine the minimum cost spanning tree

The minimum cost spanning tree of a given tree can be drawn with the help of two popular algorithms. The algorithms are named:

1. Kruskal’s algorithm
2. Prim’s algorithm

Prim’s algorithm

Prim's algorithm is used to find out the minimum cost spanning tree from a given weighted graph. We undergo the following steps to calculate a minimum cost-spanning tree using prim's algorithm.

Step – 1: Select the edge with the minimum weight in the graph. Draw the edge and its two connecting vertices (let us call it G2).

Step – 2: Examine the other edges connected to the selected vertices in step – 1. Select the edge with the minimum weight among all the edges connected to the selected vertices.

Step – 3: Confirm whether the edge selected in step – 2 does not form a loop or circle when added to the graph drawn in step – 1.

Step – 4: If it forms a loop or circle, eliminate the edge and go for the next least weighted edge connected to the vertices of graph G2 and add it to graph G2.

Step – 5: Repeat Step – 2, Step – 3, and Step – 4 until all the vertices in the given graph are covered in the graph that we drew (G2).

Therefore, we have found the minimum spanning tree of the given weighted tree.

Example:

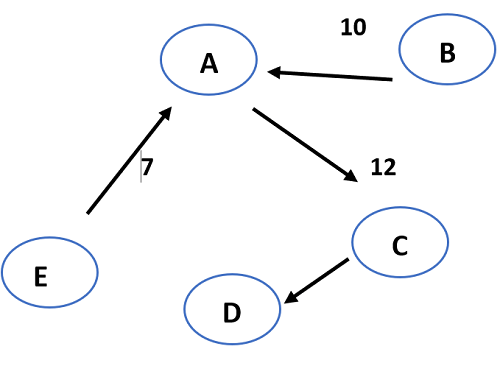
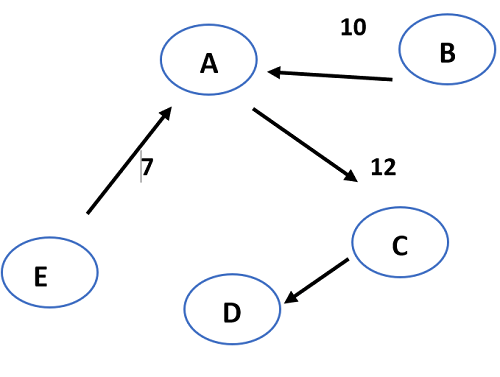
Let us find the minimum cost-spanning tree for the following using prim's algorithm:

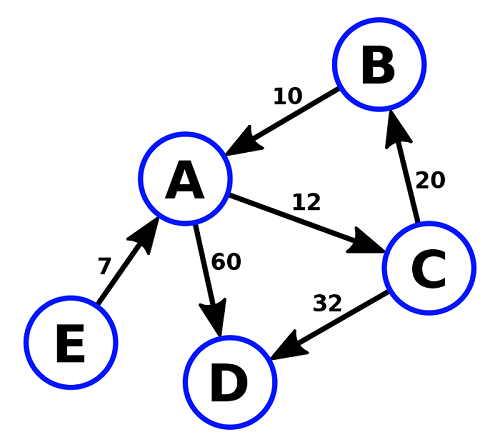
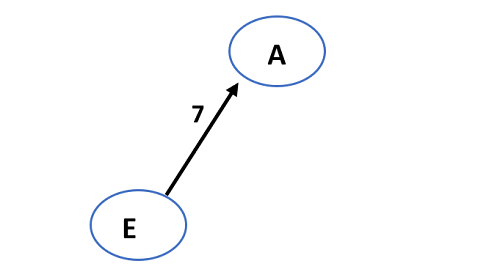
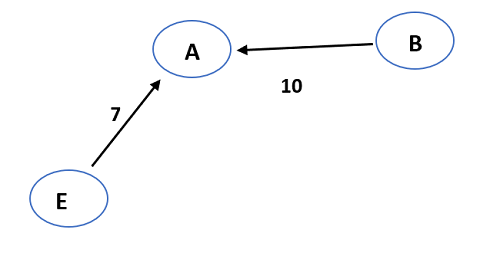
• The least weighted edge in the given graph is EA (7).

• The edge that has minimum weight compared to all the edges connected to vertices A and E is BA (10).

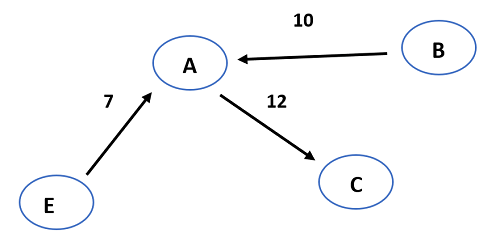
• The edge that has minimum weight compared to all the edges connected to vertices A, E, and B is AC (12).

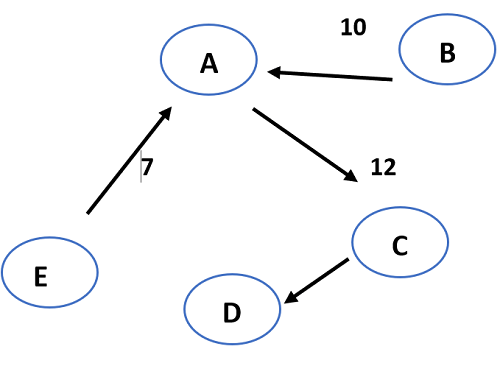
• The edge that has minimum weight compared to all the edges connected to vertices A, E, B, and C is CB (20). But BAC forms a loop.
• The next minimum weighted edge compared to all the edges connected to vertices A, E, B, and C is CD (32).

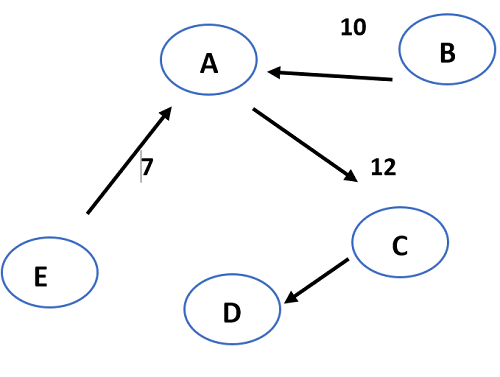
• As all the vertices of the given graph are covered, the minimum cost spanning tree of the graph is:

Kruskal’s algorithm

Kruskal's algorithm is used to find out the minimum cost-spanning tree from a given weighted graph. We undergo the following steps to calculate a minimum cost-spanning tree using prim's algorithm.

Step – 1: Select the edge with the minimum weight in the graph. Draw the edge and its two connecting vertices (let us call it G2).

Step – 2: Select the edge with the minimum weight in the given graph (Other than the one already selected). Draw the edge and its two connecting vertices (let us call it G2).

Step – 3: Confirm whether the edge selected in step – 2 does not form a loop or circle when added to the graph drawn in step – 1.

Step – 4: If it forms a loop or circle, eliminate the edge and go for the next least weighted edge with the minimum weight among the edges that are not selected.

Step – 5: Repeat Step – 2, Step – 3, and Step – 4 until all the vertices in the given graph are covered in the graph that we drew (G2).

Therefore, we have found the minimum spanning tree of the given weighted tree.

Example:

Let us find the minimum cost-spanning tree for the following using Kruskal's algorithm:

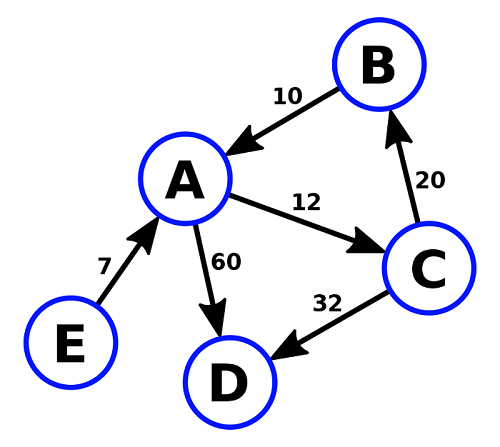
• The least weighted edge in the given graph is EA (7).

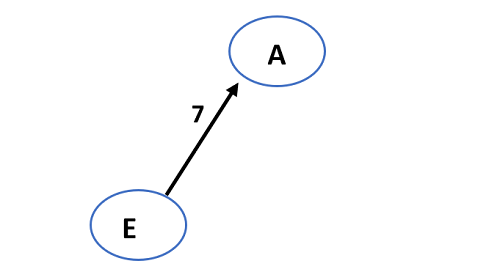
• The next edge that has minimum weight compared to all the remaining edges is BA (10).

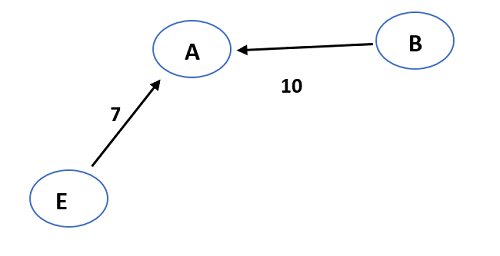
• The next edge that has minimum weight compared to all the remaining edges is AC (12).

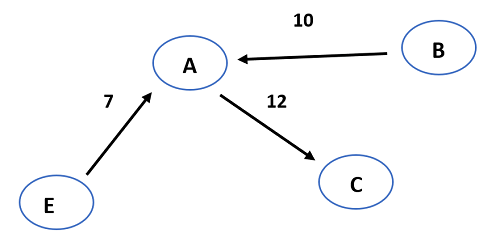
• The next edge that has minimum weight compared to all the remaining edges is CB (20). But BAC forms a loop.
• The next edge that has minimum weight compared to all the remaining edges is CD (32).

• As all the vertices of the given graph are covered, the minimum cost spanning tree of the graph is: