Red-Black Tree Insertion

A red-black tree, a type of self-balanced binary search tree, has one extra bit at each node that is typically read as a color (red or black). During insertions and deletions, the tree is balanced using these colors. Although not perfectly balanced, the tree is sufficient to shorten search times and keep the value close to O (log n), where n represents the total number of tree members.

Red Black tree was invented by Rudolf Bayer in 1972.

Note: These types of trees have the same memory footprint as traditional (uncolored) binary search trees; since each node requires only 1 bit of space to store color information.

The tree is balanced by the usage of the colors red and black. No simple path from the root to the leaf can be more than twice as long as any other such path because of node color constraints. It preserves the ability of red-black trees to balance themselves.

• The base of a red-black tree must always be black;
• Each node of a red-black tree must be either red or black.
• No two neighboring red nodes exist (a red node cannot have a red parent node or a red child node). All paths from a node (including the root) to one of NULL nodes in its descendants have the same number of black nodes.
• There are just black leaf nodes.

Insertion in Red Black Tree

A new node is always added as a RED node when it is inserted. After adding a new node, if the tree still violates the red-black tree's attributes, take the following action:

• Recolor
• Rotate
• Rotation followed by recolor.

Recolor is a node color change. So, if it's red, change it to black and vice versa.

Note: The null nodes are always black in color. Also, always try to change the color first. If color change doesn't work, go for rotation.

The insertion operation in the Red Black tree is carried out as follows...

Step 1 - Determine whether the tree is empty.

Step 2: If the tree is empty, insert the new node as the Root node with the color Black and exit the operation.

Step 3 - If the tree is not empty, add the new node as a leaf node with the color Red.

Step 4 - The process is finished if the new node's parent is Black.

Step 5: Check the color of the new node's parent node's sibling if the new node's parent node is red.

Step 6: Rotate and recolor it as necessary if it is black or NULL.

Step 7: If it's red, change the color. Repeat until the tree becomes a Red Black Tree.

Algorithm for node insertion

The steps are as follows to add a new element to the red-black tree:

• Assume that x is the tree's root and that y represents a leaf (i.e., NIL).
• Verify that the tree is empty (that is; if x is NULL). If so, add a new node as the root node and make it black. Otherwise, repeat these steps until you reach a leaf (NIL).
•  Compare the new Key and root Key.
• Navigate to the appropriate subtree if a new Key is bigger than the root Key.
• If not, proceed via the left subtree.
• Assign the leaf's parent as the new node's parent. If the leaf Key is greater than the new Key, make the new node the right Child.
  Otherwise, create the new node as the left child.
• Assign NULL to the new node's left and right children.
• Give the new node the colour RED. Call the Insert fix algorithm to preserve    properties of the red-black tree on the violation.

Example: Insert the following series of numbers to create a red-black tree.
9, 19, 6, 16, 18

• STEP 1: Insert (9)
  The tree is empty. So, insert a new node as the black root node.

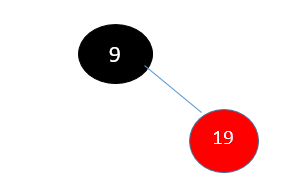
• STEP 2: Insert (19)
  The tree is not empty in step two; insert (19). So, add a new red-colored node.

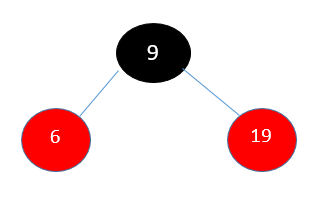
• STEP 3: Insert (6)
  In step three, put (6).

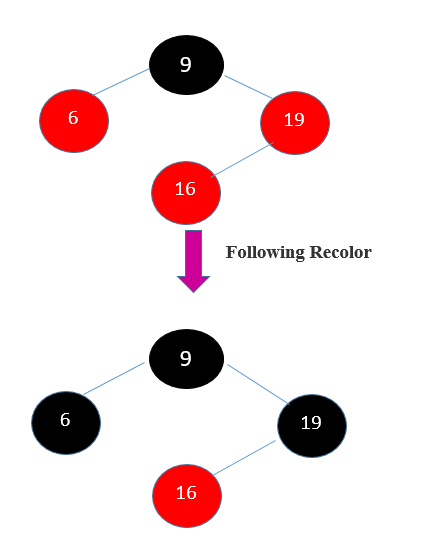
 STEP 4: Insert (16)
Insert (16) in Step 4, as the tree is not empty, Add a new node with the color red.

 STEP 5: Insert (18)
Insert (18) in Step 5. The tree is not empty.

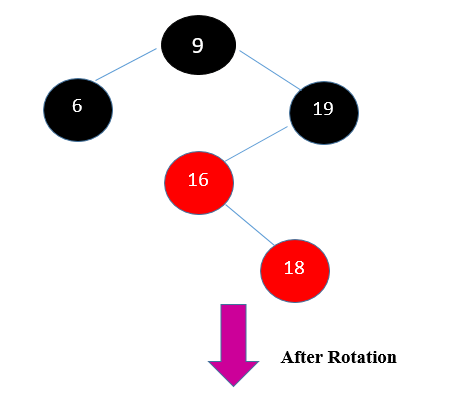
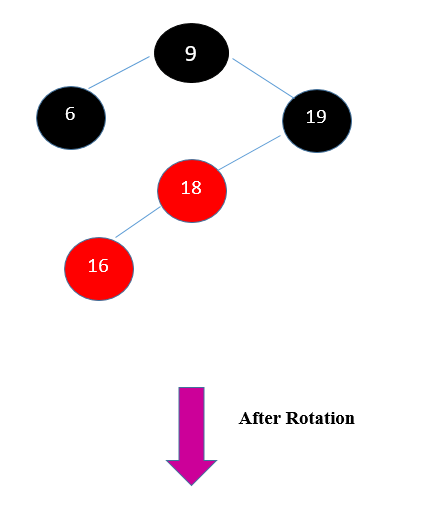
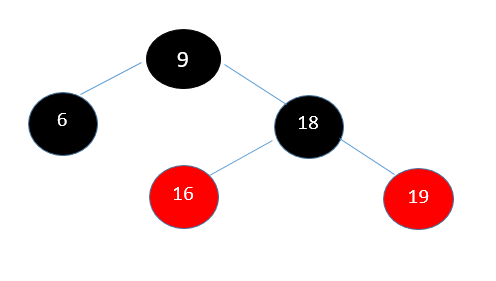
Hence Insertion is done in the red-black tree.