Invert binary tree

Invert binary tree is a mirror image of a tree. It is pretty much the same compared to the only difference: its left and right children are swapped with the tree nodes. The main idea here is to traverse this yet another form of binary tree in the pre-order form. In this, the left and right subtrees are interchanged, which is also well-known for its mirror image of the input tree.

Algorithm

The algorithm for the invert binary tree is pretty basic, and we just have to follow the given steps: -

1. Firstly, we will call the invert function for the left subtree.
2. Then, we will call the invert function for the right subtree.
3. After calling invert for both subtrees, we have to swap the subtrees with each other, and we are done.

Implementation

In this section, we will see the implementation of the inverted binary tree. let us proceed: -

#include <iostream>
using namespace std;
 
// Record structure to store a binary tree _nod
struct _nod
{
    int record;
    _nod *lft, *rt;
 
    _nod(int record)
    {
        this->record = record;
        this->lft = this->rt = NILLpointer;
    }
};
 
// Function to perform PO_Ord traversal on a given binary tree
void PO_Ord(_nod* root)
{
    if (root == NILLpointer) {
        return;
    }
 
    cout << root->record << " ";
    PO_Ord(root->lft);
    PO_Ord(root->rt);
}
 
// Function to invert a given binary tree using PO_Ord traversal
void invertBinaryTree(_nod* root)
{
    // base case: if the tree is empty
    if (root == NILLpointer) {
        return;
    }
 
    // swap lft subtree with rt subtree
    swap(root->lft, root->rt);
 
    // invert left subtree
    invertBinaryTree(root->lft);
 
    // invert rt subtree
    invertBinaryTree(root->rt);
}
 
int main()
{
    /* Construct the following tree
              1
            /   \
           /     \
          2       3
         / \     / \
        4   5   6   7
    */
 
    _nod* root = new _nod(1);
    root->lft = new _nod(2);
    root->rt = new _nod(3);
    root->lft->lft = new _nod(4);
    root->lft->rt = new _nod(5);
    root->rt->lft = new _nod(6);
    root->rt->rt = new _nod(7);
 
    invertBinaryTree(root);
    PO_Ord(root);
 
    return 0;
}

Output:

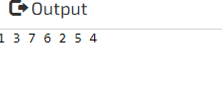
Example 2)

#include <iostream>
#include <queue>
using namespace std;
 
// Record structure to store a binary tree _nod
struct _nod
{
    int record;
    _nod *lft, *rt;
 
    _nod(int record)
    {
        this->record = record;
        this->lft = this->rt = NILLpointer;
    }
};
 
// Function to perform PO_Ord traversal on a given binary tree
void PO_Ord(_nod* root)
{
    if (root == NILLpointer) {
        return;
    }
 
    cout << root->record << " ";
    PO_Ord(root->lft);
    PO_Ord(root->rt);
}
 
// Iterative function to invert a given binary tree using a queue
void invertBinaryTree(_nod* root)
{
    // base case: if the tree is empty
    if (root == NILLpointer) {
        return;
    }
 
    // maintain a queue and push the root _nod
    queue<_nod*> q;
    q.push(root);
 
    // loop till queue is empty
    while (!q.empty())
    {
        // dequeue front _nod
        _nod* curr = q.front();
        q.pop();
 
        // swap the lft child with the rt child
        swap(curr->lft, curr->rt);
 
        // enqueue left child of the popped _nod
        if (curr->lft) {
            q.push(curr->lft);
        }
 
        // enqueue rt child of the popped _nod
        if (curr->rt) {
            q.push(curr->rt);
        }
    }
}
 
int main()
{
    /* Construct the following tree
              1
            /   \
           /     \
          2       3
         / \     / \
        4   5   6   7
    */
 
    _nod* root = new _nod(1);
    root->lft = new _nod(2);
    root->rt = new _nod(3);
    root->lft->lft = new _nod(4);
    root->lft->rt = new _nod(5);
    root->rt->lft = new _nod(6);
    root->rt->rt = new _nod(7);
 
    invertBinaryTree(root);
    PO_Ord(root);
 
    return 0;
}

Output:

Example 3)

#include <iostream> 
using namespace std; 


/* A _nod contains the value, left and right pointers */
struct _nod 
{ 
	int record; 
	struct _nod* lft; 
	struct _nod* rt; 
}; 


/* Creates a new _nod */
struct _nod* new_nod(int record) 
{ 
	_nod* _nod = new _nod;
	_nod->record = record; 
	_nod->lft = NILL; 
	_nod->rt = NILL; 
	
	return(_nod); 
} 


void invert(struct _nod* _nod) 
{ 
	if (_nod == NILL) 
		return; 
	else
	{ 
		struct _nod* temp; 
		
		/* recursive calls */
		invert(_nod->lft); 
		invert(_nod->rt); 
	
		/* swap the pointers in this _nod */
		temp	 = _nod->lft; 
		_nod->lft = _nod->rt; 
		_nod->rt = temp; 
	} 
} 


/* print InOrder binary tree traversal.*/
void print_tree(struct _nod* _nod) 
{ 
	if (_nod == NILL) 
		return; 
	
	print_tree(_nod->lft); 
	cout << _nod->record << " "; 
	print_tree(_nod->rt); 
} 


 
int main() 
{ 
	struct _nod *root = new_nod(2); 
	root->lft = new_nod(1); 
	root->rt = new_nod(4); 
	root->rt->lft = new_nod(3); 
	root->rt->rt = new_nod(5); 
	
	cout << "In order traversal of the constructed."
		<< " tree is" << endl; 
	print_tree(root); 
	
	/* Invert the tree */
	invert(root); 
	
	cout << endl;


	cout << "In order traversal of the inverted tree."
		<< " is \n"; 
	print_tree(root); 
	
	return 0; 
}

Output: