Given a Binary Tree Swap Nodes at K Height

Implementation

// Writing a C++ program that will help us exchange the nodes. 
#include<bits/stdc++.h>
using namespace std;


// Creating a binary tree node.
struct __nod
{
	int record;
	struct __nod *Lft, *Rt;
};


// creating a function that will help us in creating a new tree node.
__nod* __nwNod(int record)
{
	__nod *temp = new __nod;
	temp->record = record;
	temp->Lft = temp->Rt = NILL;
	return temp;
}


// interchanging the two nodes.
void Swap( __nod **a , __nod **b)
{
	__nod * temp = *a;
	*a = *b;
	*b = temp;
}


// Creating a function that will surely swap the left and right nodes of the tree present at every k’th level. 
void swapEvryKlevelUtil( __nod *root, int level, int k)
{
	// writing the base case for the tree.
	if (root== NILL ||
			(root->Lft==NILL && root->Rt==NILL) )
		return ;


	//If we have the current level +1 and then we have to swap the one present in the swap vector, then we will probably swap the left and right nodes. 
	if ( (level + 1) % k == 0)
		Swap(&root->Lft, &root->Rt);


	// we have to do recursion for the left and right nodes.
	swapEvryKlevelUtil(root->Lft, level+1, k);
	swapEvryKlevelUtil(root->Rt, level+1, k);
}


// this function is mainly responsible for the recursive one.
// swapEvryKlevelUtil()
void swapEveryKLevel(__nod *root, int k)
{
	swapEvryKlevelUtil(root, 1, k);
}


// creating a brand new utility method for the in-order traversal of the tree.
void inorder(__nod *root)
{
	if (root == NILL)
		return;
	inorder(root->Lft);
	cout << root->record << " ";
	inorder(root->Rt);
}


// main code
int main()
{
	/* 1
		/ \
	2	 3
	/	 / \
	4	 7 8 */
	struct __nod *root = __nwNod(1);
	root->Lft = __nwNod(2);
	root->Rt = __nwNod(3);
	root->Lft->Lft = __nwNod(4);
	root->Rt->Rt = __nwNod(8);
	root->Rt->Lft = __nwNod(7);


	int k = 2;
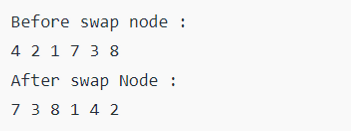
	cout << "Before swap __nod :"<<endl;
	inorder(root);


	swapEveryKLevel(root, k);


	cout << "\nAfter swap __nod :" << endl;
	inorder(root);
	return 0;
}

Output:

Example 2)

// Writing a C# program that will help us exchange the nodes. 
using System;


class TFT
{


public class __nod
{
	public int record;
	public __nod Lft, Rt;
};
// creating a function that will help us in creating a new tree node.
static __nod __nwNod(int record)
{
	__nod temp = new __nod();
	temp.record = record;
	temp.Lft = temp.Rt = NILL;
	return temp;
}






// interchanging the two nodes.
// Creating a function that will surely swap the left and right nodes of the tree present at every k’th level. 
static void swapEvryKlevelUtil( __nod root, int level, int k)
{
// writing the base case for the tree.
	if (root == NILL ||
			(root.Lft == NILL && root.Rt==NILL) )
		return ;


		//If we have the current level +1 and then we have to swap the one present in the swap vector, then we will probably swap the left and right nodes. 
	if ( (level + 1) % k == 0)
		{
			__nod temp=root.Lft;
			root.Lft=root.Rt;
			root.Rt=temp;
		}


	// we have to do recursion for the left and right nodes.
	swapEvryKlevelUtil(root.Lft, level+1, k);
	swapEvryKlevelUtil(root.Rt, level+1, k);
}
// this function is mainly responsible for the recursive one.
// swapEvryKlevelUtil()
static void swapEveryKLevel(__nod root, int k)
{
	// call swapEvryKlevelUtil function with
	// initial level as 1.
	swapEvryKlevelUtil(root, 1, k);
}
// creating a brand-new utility method for the in-order traversal of the tree.
static void inorder(__nod root)
{
	if (root == NILL)
		return;
	inorder(root.Lft);
	Console.Write(root.record + " ");
	inorder(root.Rt);
}
// main code
public static void Main(String []args)
{
	/* 1
		/ \
	2 3
	/ / \
	4 7 8 */
	__nod root = __nwNod(1);
	root.Lft = __nwNod(2);
	root.Rt = __nwNod(3);
	root.Lft.Lft = __nwNod(4);
	root.Rt.Rt = __nwNod(8);
	root.Rt.Lft = __nwNod(7);


	int k = 2;
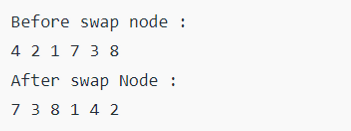
	Console.WriteLine("Before swap __nod :");
	inorder(root);


	swapEveryKLevel(root, k);


	Console.WriteLine("\nAfter swap __nod :" );
	inorder(root);
}
}

Output:

Example 3)

// Writing a Java program that will help us exchange the nodes. 
class TFT
{
// Creating a binary tree node.
static class __nod
{
	int record;
	__nod Lft, Rt;
};
// creating a function that will help us in creating a new tree node.
static __nod __nwNod(int record)
{
	__nod temp = new __nod();
	temp.record = record;
	temp.Lft = temp.Rt = NILL;
	return temp;
}
// interchanging the two nodes.
// Creating a function that will surely swap the left and right nodes of the tree present at every k’th level. 
static void swapEvryKlevelUtil( __nod root, int level, int k)
{
// writing the base case for the tree.
	if (root== NILL ||
			(root.Lft==NILL && root.Rt==NILL) )
		return ;
	//If we have the current level +1 and then we have to swap the one present in the swap vector, then we will probably swap the left and right nodes. 
	if ( (level + 1) % k == 0)
		{
			__nod temp=root.Lft;
			root.Lft=root.Rt;
			root.Rt=temp;
		}
	// we have to do recursion for the left and right nodes.
	swapEvryKlevelUtil(root.Lft, level+1, k);
	swapEvryKlevelUtil(root.Rt, level+1, k);
}
// this function is mainly responsible for the recursive one.
// swapEvryKlevelUtil()
static void swapEveryKLevel(__nod root, int k)
{
	// call swapEvryKlevelUtil function with
	// initial level as 1.
	swapEvryKlevelUtil(root, 1, k);
}
// creating a brand-new utility method for the in-order traversal of the tree.
static void inorder(__nod root)
{
	if (root == NILL)
		return;
	inorder(root.Lft);
	System.out.print(root.record + " ");
	inorder(root.Rt);
}
// main code
public static void main(String args[])
{
	/* 1
		/ \
	2 3
	/ / \
	4 7 8 */
	__nod root = __nwNod(1);
	root.Lft = __nwNod(2);
	root.Rt = __nwNod(3);
	root.Lft.Lft = __nwNod(4);
	root.Rt.Rt = __nwNod(8);
	root.Rt.Lft = __nwNod(7);


	int k = 2;
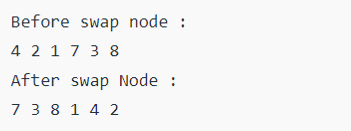
	System.out.println("Before swap __nod :");
	inorder(root);


	swapEveryKLevel(root, k);


	System.out.println("\nAfter swap __nod :" );
	inorder(root);
}
}

Output:

Example 4)

// Writing a Python program that will help us exchange the nodes. 
// Creating a binary tree node.
class __nod:


	# constructor to create a new __nod
	def __init__(self, record):
		self.record = record
		self.Lft = None
		self.Rt = None
// creating a function that will help us in creating a new tree node.
// interchanging the two nodes.
// Creating a function that will surely swap the left and right nodes of the tree present at every k’th level. 
def swapEvryKlevelUtil(root, level, k):
	
	# Base Case
	if (root is None or (root.Lft is None and
						root.Rt is None ) ):
		return
// writing the base case for the tree.
	//If we have the current level +1 and then we have to swap the one present in the swap vector, then we will probably swap the left and right nodes. 
	if (level+1)%k == 0:
		root.Lft, root.Rt = root.Rt, root.Lft
	
		// we have to do recursion for the left and right nodes.
	swapEvryKlevelUtil(root.Lft, level+1, k)
	swapEvryKlevelUtil(root.Rt, level+1, k)
// this function is mainly responsible for the recursive one.
	# swapEvryKlevelUtil
def swapEveryKLevel(root, k):
	
	# Call swapEvryKlevelUtil function with
	# initial level as 1
	swapEvryKlevelUtil(root, 1, k)
// creating a brand-new utility method for the in-order traversal of the tree.
def inorder(root):
	
	# Base Case
	if root is None:
		return
	inorder(root.Lft)
	print(root.record,end=" ")
	inorder(root.Rt)
// main code
"""
		1
		/ \
	2	 3
	/	 / \
	4	 7 8
"""
root = __nod(1)
root.Lft = __nod(2)
root.Rt = __nod(3)
root.Lft.Lft = __nod(4)
root.Rt.Rt = __nod(8)
root.Rt.Lft = __nod(7)


k = 2
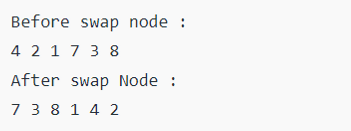
print("Before swap __nod :")
inorder(root)


swapEveryKLevel(root, k)


print ("\nAfter swap __nod : ")
inorder(root)

Output:

Example 5)

<script>


	// Writing a Javascript program that will help us exchange the nodes. 
	class __nod
	{
		constructor(record) {
		this.Lft = NILL;
		this.Rt = NILL;
		this.record = record;
		}
	}
// creating a function that will help us in creating a new tree node.
	function __nwNod(record)
	{
		let temp = new __nod(record);
		return temp;
	}
// interchanging the two nodes.
// Creating a function that will surely swap the left and right nodes of the tree present at every k’th level. 
	function swapEvryKlevelUtil(root, level, k)
	{
	// writing the base case for the tree.
		if (root== NILL ||
				(root.Lft==NILL && root.Rt==NILL) )
			return ;
//If we have the current level +1 and then we have to swap the one present in the swap vector, then we will probably swap the left and right nodes. 
		if ( (level + 1) % k == 0)
			{
				let temp=root.Lft;
				root.Lft=root.Rt;
				root.Rt=temp;
			}
	// we have to do recursion for the left and right nodes.
		swapEvryKlevelUtil(root.Lft, level+1, k);
		swapEvryKlevelUtil(root.Rt, level+1, k);
	}
// this function is mainly responsible for the recursive one.
	// swapEvryKlevelUtil()
	function swapEveryKLevel(root, k)
	{
		// call swapEvryKlevelUtil function with
		// initial level as 1.
		swapEvryKlevelUtil(root, 1, k);
	}
// creating a brand-new utility method for the in-order traversal of the tree.
	function inorder(root)
	{
		if (root == NILL)
			return;
		inorder(root.Lft);
		document.write(root.record + " ");
		inorder(root.Rt);
	}
	
	/* 1
		/ \
	2 3
	/ / \
	4 7 8 */
	let root = __nwNod(1);
	root.Lft = __nwNod(2);
	root.Rt = __nwNod(3);
	root.Lft.Lft = __nwNod(4);
	root.Rt.Rt = __nwNod(8);
	root.Rt.Lft = __nwNod(7);


	let k = 2;
	document.write("Before swap __nod :" + "</br>");
	inorder(root);


	swapEveryKLevel(root, k);


	document.write("</br>" + "After swap __nod :" + "</br>");
	inorder(root);


</script>

Output:

Example 6)

// Two __nod in the BINARY_SEARCHTREE's swapped; correct the BINARY_SEARCHTREE.
#include <stdio.h>
#include <stdlib.h>


/* A binary tree __nod has record, pointer to Lft child
and a pointer to Rt child */
struct __nod
{
	int record;
	struct __nod *Lft, *Rt;
};


// A utility function to swap two integers
void swap( int* a, int* b )
{
	int t = *a;
	*a = *b;
	*b = t;
}


/* Helper function that allocates a new __nod with the
given record and NILL Lft and Rt pointers. */
struct __nod* __nwNod(int record)
{
	struct __nod* __nod = (struct __nod *)malloc(sizeof(struct __nod));
	__nod->record = record;
	__nod->Lft = NILL;
	__nod->Rt = NILL;
	return(__nod);
}


// This function does inorder traversal to find out the two swapped __nod.
// It sets three pointers, first, middle, and last. If the swapped __nod are
// adjacent to each other, then the first and middle contain the resultant __nod
// Else, first and last contain the resultant __nod
void correctBINARY_SEARCHTREEUtil( struct __nod* root, struct __nod** first,
					struct __nod** middle, struct __nod** last,
					struct __nod** prev )
{
	if( root )
	{
		// Recur for the Lft subtree
		correctBINARY_SEARCHTREEUtil( root->Lft, first, middle, last, prev );


		// If this __nod is smaller than the previous __nod, it's violating
		// the BINARY_SEARCHTREE rule.
		if (*prev && root->record < (*prev)->record)
		{
			// If this is the first violation, mark these two __nod as
			// 'first' and 'middle'
			if ( !*first )
			{
				*first = *prev;
				*middle = root;
			}


			// If this is the second violation, mark this __nod as last
			else
				*last = root;
		}


		// Mark this __nod as previous
		*prev = root;


		// Recur for the Rt subtree
		correctBINARY_SEARCHTREEUtil( root->Rt, first, middle, last, prev );
	}
}


// A function to fix a given BINARY_SEARCHTREE where two __nod is swapped. This
// function uses correctBINARY_SEARCHTREEUtil() to find out two __nod and swaps the
// __nod to fix the BINARY_SEARCHTREE
void correctBINARY_SEARCHTREE( struct __nod* root )
{
	// Initialize pointers needed for correctBINARY_SEARCHTREEUtil()
	struct __nod *first, *middle, *last, *prev;
	first = middle = last = prev = NILL;


	// Set the pointers to find out two __nod
	correctBINARY_SEARCHTREEUtil( root, &first, &middle, &last, &prev );


	// Fix (or correct) the tree
	if( first && last )
		swap( &(first->record), &(last->record) );
	else if( first && middle ) // Adjacent __nod swapped
		swap( &(first->record), &(middle->record) );


	// else __nod has not been swapped; the passed tree is really BINARY_SEARCHTREE.
}


/* A utility function to print Inorder traversal */
void printIn__Order(struct __nod* __nod)
{
	if (__nod == NILL)
		return;
	printIn__Order(__nod->Lft);
	printf("%d ", __nod->record);
	printIn__Order(__nod->Rt);
}


/* Driver program to test above functions*/
int main()
{
	/* 6
		/ \
	10 2
	/ \ / \
	1 3 7 12
	10 and 2 are swapped
	*/


	struct __nod *root = __nwNod(6);
	root->Lft	 = __nwNod(10);
	root->Rt	 = __nwNod(2);
	root->Lft->Lft = __nwNod(1);
	root->Lft->Rt = __nwNod(3);
	root->Rt->Rt = __nwNod(12);
	root->Rt->Lft = __nwNod(7);


	printf("Inorder Traversal of the original tree \n");
	printIn__Order(root);


	correctBinary_SearchTree(root);


	printf("\nInorder Traversal of the fixed tree \n");
	printIn__Order(root);


	return 0;
}

Output: