Number of visible boxes putting one inside another

You have given one array, which consists of values which represent the sizes of different boxes. We can put one box inside another if the size of the outside box is two times or greater than inside box. You have to find out the number of boxes which are at last visible. Let’s take an example -

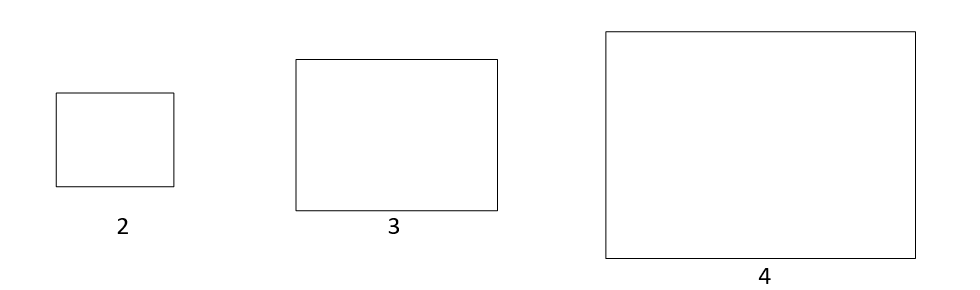
For the above diagram, we have three boxes, and their sizes are 2, 3, and 4.

Input-  

2, 3, 4

Output-

2

Explanation- We can put box 2 inside of 4 because its size is greater than 2. Now remaining boxes are 3 and 4. So, the number of boxes is 2.

Algorithm:-

Step 1: Start

Step 2: The value which represents the number of boxes is taken from the user.

Step 3: An array is created of size n. Then values of the array are taken from the user.

Step 4: A function is called to calculate the answer.

Step 5: In this function, we take the input value and the array.

Step 6: The answer is calculated.

Step 7: The value of the answer is returned.

Step 8: The returned value will be printed.

Step 9: Stop.

Explanation of Algorithm: - To solve this problem, we will sort the array. In the function, we create a queue to represent the element which will be visible at the end. We simply traverse the array, and if any element is found which is greater than the front element of the queue, then the front element will be deleted. After the ending of traversal, we get the elements which will be visible. The answer will be the size of the queue.

Code: -

// program in cpp to calculate the number of remaining boxes after putting one inside another.
#include <bits/stdc++.h>
using namespace std;
int fun (int array[], int n)
{
	queue<int> q;
	sort(array, array + n);
	q.push(array[0]);
	for (int i = 1; i < n; i++) {


		int now = q.front();
// deletion of front element of queue if the traversing element is double times or 
//greater than queue
		if (array[i] >= 2 * now)
			q.pop();
		q.push (array[i]);
	}


	return q.size();
}
int main()
{
	int arr[] = { 2, 3, 4};
	int n = sizeof(arr) / sizeof(arr[0]);
	cout << fun(arr, n) << endl;
	return 0;
}

Program in Java

// program in java to calculate the number of remaining boxes after putting one inside another.
import java.util.LinkedList;
import java.util.Queue;
import java.util.Arrays;
public class jtp {
	static int minimumBox(int []arr, int n)
	{		
		Queue<Integer> q = new LinkedList<>();	
		Arrays.sort(arr);	
		q.add(arr[0]);		
		for (int i = 1; i < n; i++)
		{
			int now = q.element();
	// deletion of front element of queue if the traversing element is double times or
 //greater than queue
			if (arr[i] >= 2 * now)
			q.remove();
			q.add(arr[i]);
		}
		return q.size();
	}
	
	// Driver code
	public static void main(String args[])
	{
		int [] arr = { 2, 3, 4};
		int n = arr.length;		
		System.out.println(minimumBox(arr, n));
	}
}

Program in Python

# program in python to calculate the number of remaining boxes after putting one inside another.

import collections
def fun (arr, n):
	q = collections.deque([])
	# sorting the array
	arr.sort()
	q.append(arr[0])
	# traversing the array
	for i in range(1, n):
		now = q[0]
		# deletion of front element of queue if the traversing element is double times or #greater than queue
		if(arr[i] >= 2 * now):
			q.popleft()
		# Pushing each element of array
		q.append(arr[i])
	return len(q)
if __name__=='__main__':
	arr = [2, 3, 4]
	n = len(arr)
	print(fun (arr, n))

Program in JavaScript

// program in JavaScript to calculate the number of remaining boxes after putting one inside another.

<script>
function minimumBox(arr, n)
{
	var q = [];
	arr.sort((a,b)=> a-b)
	q.push(arr[0]);
	// array traversal
	for (var i = 1; i < n; i++) {
		var now = q[0];
		// deletion of front element of queue if the traversing element is double times or //greater than queue
		if (arr[i] >= 2 * now)
			q.pop(0);
		q.push(arr[i]);
	}
	return q.length;
}
var arr = [2, 3, 4];
var n = arr.length;
document.write( minimumBox(arr, n));
</script>

Output:

2

Complexity Analysis: -

Time complexity- Here, we need looping and sorting. For sorting, logn time will be taken and for traversing n time is taken. So, we can find the solution within nlogn time. Time complexity will be O (nlogn).