Introduction to 2D-Arrays

Two Dimensional Array

Technical Definitions

An array of arrays is a common definition for a two-dimensional array. A matrix is another name for a two-dimensional array. A matrix looks like a table with rows and columns.

What is the syntax for declaring a two-dimensional array?

Defining a 2D array is fairly similar to declaring a 1D array in terms of syntax.

Syntax.

int arr[max_rows][max_columns];

As demonstrated below, it generates the following data structure:

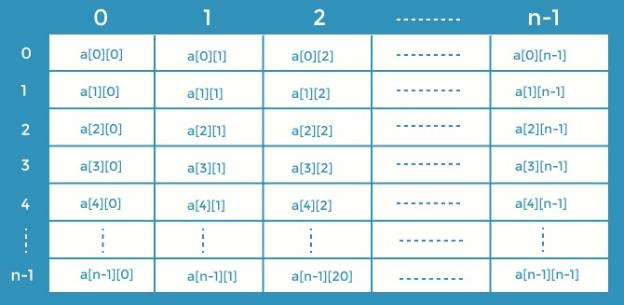
How do you get data from a 2D array?

In the same way that data may be accessed using simply an index in a one-dimensional array, the indices of the cells can be used to access the cells individually in a two-dimensional array. A single cell has two indices: one is its row number, and the other is its column number.

The value recorded in any cell of an array is stored using the following syntax —

int x = a[i][j];

The row and column indices are I and j, respectively.

Creating a 2D array —

When declaring a one-dimensional array, we don't need to mention its size, but this isn't the case with a two-dimensional array. We must define at least the row size, or the second dimension, for a 2D array.

2D array declaration syntax —

int arr[2][2] = {1,2,3,4}

In a 2D array, the number of items is always equal to (number of rows * number of columns).

Consider the following scenario:

#include<stdio.h>
void main()
{
    int array[4][4],i,j;
    for (i=0; i<4; i++)
    {
        for (j=0; j<4; j++)
        {
            printf(“Enter value for array[%d][%d]: “ i,j);
            scanf(“%d”,&array[i][j]);
        }
    }
}

One-Dimensional (1D) Array vs. Two-Dimensional (2D) Array

Concept.	One-Dimensional (1D) Array	Two-Dimensional (2D) Array
Meaning	A one-dimensional array stores a single list of related data components.	A list of lists or an array of arrays is kept in a two-dimensional array.
Size	Total Bytes = sizeof(datatype of array variable)* size of array is the size of a one-dimensional (1D) array.	Total Bytes= sizeof(datatype of array variable)* size of first index* size of second index is the size of a two-dimensional (2D) array.
Dimension	A one-dimensional array (sometimes known as a 1D array) has only one dimension.	The dimension of a two-dimensional (2D) array is two.
Row column matrix	In a one-dimensional (1D) array, there is no row column matrix.	In a two-dimensional (2D) array, there is a row and column matrix.

Addressing of 2-D Array

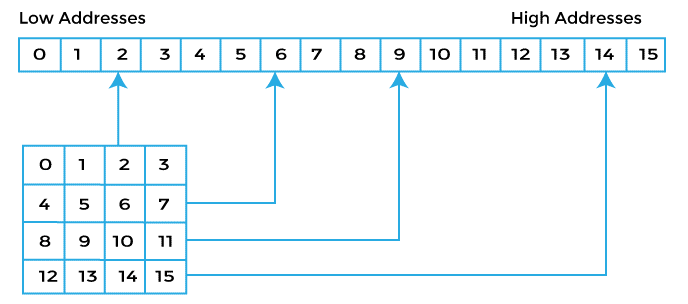
Row Major Order:

In an array, row major ordering is as follows:-

Row major ordering sends subsequent components to successive memory locations, travelling across the rows and then down the columns.

If the items of an array are stored in a Row-Wise form, in simple terms. The following diagram illustrates this mapping:

For a two-dimensional row-major ordered array, the formula to determine the Address (offset) is:

Address of A[I][J] = Base Address + W * ( C * I + j)

Where Base Address is the address of an array's first element.

• W stands for data type's weight (size).
• C stands for the total number of columns.
• I stands for the row number
• J stands for the column number of the element whose address has to be determined.

Column Major Ordering:

Column-major ordering in an array is when the elements of an array are stored in a Column Wise form. As you progressed through successive memory regions in row-major ordering, the rightmost index rose the fastest. The leftmost index advances the fastest in column-major ordering.

A column-major ordered array is seen in the diagram below.

Address of A[I][J] = Base Address + W * ( R * J + I)

Where Base Address is the address of an array's first element.

• W stands for data type's weight (size).
• R stands for the total number of rows.
• I stands for the row number
• J stands for the column number of the element whose address has to be determined.