B Tree in Data Structure

Data management is called database management. A data model is a system that stores, manages, and optimizes computer resources. Data processing is not just about data storage. Almost every app or program has notices and updates about its version. Data structures are so simple and complex that it is difficult to program with a programming language that does not have data structures.

Data processing is the process of using intelligence and software to manage, organize, store and store information on a computer device or system. Data models provide visualization for easy data organization and management. Any basic process, program, or program has two parts: data and algorithms - the rules and regulations of data exchange and algorithms.

There are two types of data structures:

1. Linear Data structures.
2. Non-linear data structures.

Linear Data structures

This data type adds data to the data type. It's all about the process. You can then delete the duplicate. There are four types of linear data, they are:

1. Queue
2. Stack
3. Linked lists
4. Array

Non-Linear Data structures

Data formats can be created in a variety of ways. There are two types of interpersonal communication:

1. Tree data structure
2. Graph data structure

Tree data structures

A non–linear data structure that is hierarchical is known as the tree data structure. A node of a tree can have any number of children. Numerous data structures are used in computer science to organize data into different formats. One of them that simulates a hierarchical tree structure and is extensively used is a tree. A tree typically consists of a root value and child nodes that branch out of its parent nodes to form subtrees. Non-linear data structures include trees.

There is no cap on how many child nodes a standard tree data structure can store. However, with a binary tree, this is not the case. The binary Tree and its various varieties are a particular tree data structure that will be covered in this article.

 A tree data structure is classified into six types:

1. Available trees.
2. Binary trees.
3. Binary search trees.
4. AVL tress (Adelson, Velsky and Em Landis tree).
5. Red – Black Tree.
6. N – ary Tree.

B tree

One of the primary benefits of adopting a B tree is its ability to hold many keys in a single node and tremendous fundamental values while maintaining a relatively small tree height.

Although each node must have m/2 nodes, they are not required to all have the same number of children.

Any B Tree property, such as the minimum number of children a node can have, may be violated while executing certain actions on the B Tree.

Operations performed in B tree

Searching

Similar to binary search trees, B trees also allow for searching. For instance, look in the following B Tree for the item:

1. Go to the sub-tree on its left because 49 78.
2. Travel via the right sub-tree of 40 because 404956. 3. 49>45, travel to the right. 48 through 49.
3. If a match is made, go back.

Inserting

At the level of the leaf node, insertions are made. Explore the B Tree to determine the proper leaf node where the node should be put.

1. After insertion in ascending order, if the leaf node does not contain m-1 keys, go to step 4.
   1. Add the new element to the elements' increasing order.
   2. Divide the node at the median into two nodes.
   3. Move the middle element to the top of its parent node.
   4. Split the parent node using the same procedures if it has m-1 keys.

Example:

The B Tree of order 5 in the accompanying graphic needs to add node eight.

Put 8 in since it will be placed to the right of 5.

The number of keys in the node has increased from (5 -1 = 4) keys to 5.

Deletion

The leaf nodes also engage in deletion. A leaf node or an internal node might be the node that has to be eliminated. Take the element from eight or the left sibling to finish the keys if the leaf node lacks m/2 keys.

1. Move the element between the left sibling's most significant element and its parent to the node where the key is erased if the left sibling includes more than m/2 items.
2. Join two leaf nodes and the parent node's intermediary element to form a new leaf node if none of the siblings contain more than m/2 elements.
3. Apply the technique mentioned above to the parent if there are less than m/2 nodes left.

Example 1

In the B Tree of order five illustrated in the accompanying image, remove node 53.

The right child of element 49 contains 53. Please remove it.

Since there is currently only one element left in node 57, and a B tree of order 5 requires a minimum of two elements, neither the left nor right subtrees contain enough elements to satisfy this requirement. As a result, merge the remaining element with the parent's left sibling and intervening element, 49.

Finished B tree.

Applications of B tree

Since accessing values in a vast database saved on a disc takes a long time, B trees index the data and allow quick access to the data stored on the discs.

In the worst scenario, it takes O(n) running time to search a database with n key values that are not sorted or indexed. The worst-case scenario for searching this database is O(log n) time if we use B Tree as the indexing method.

B+ Tree

A B Tree extension called B+ Tree enables effective search, insertion, and deletion operations.

Contrarily, records (data) can only be kept on leaf nodes in a B+ tree, while inside nodes can only hold key values.

To improve the effectiveness of search queries, the leaf nodes of a B+ tree are linked together as singly linked lists.

The enormous quantity of data that cannot be kept in the main memory is saved in B+ Trees.

The B+ Tree's interior nodes are frequently referred to as index nodes. The picture below depicts a B+ tree of rank 3.

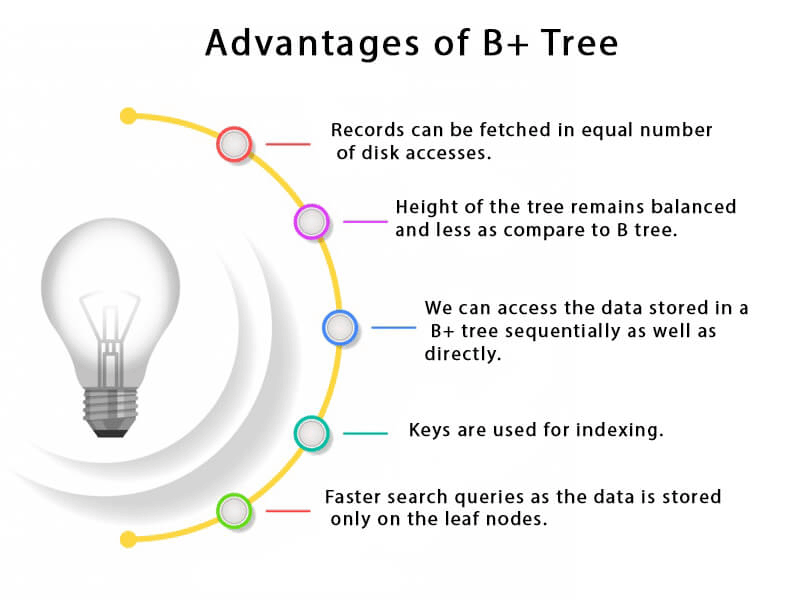
Advantages of B+ Tree

1. The number of disc accesses required to obtain a record must be equal.
2. The Tree's height is still balanced and lower than the B tree.
3. We have direct and sequential access to the data kept in a B+ tree.
4. Indexing is done using keys.
5. Quicker search results since data are only saved on leaf nodes.

B tree vs. B+ Tree

B tree	B+ Tree
1) Search keys cannot be saved more than once. 2) Both internal nodes and leaf nodes can be used to store data. 3) Since information may be located on internal and leaf nodes, searching for some data takes longer. 4) Leaf nodes can't be connected.	1) Multiple redundant search keys may exist. 2) Only the leaf nodes may hold data. 3) Since information can only be discovered on leaf nodes, searching is often faster. 4) Since elements are permanently eliminated from the leaf nodes, deletion will never be a complicated procedure. 5) To increase the effectiveness of the search operations, leaf nodes are connected.

Insertion in B+ Tree

1. Place the new node as a leaf node in the first step.
2. Step 2: Split the node and copy the center node to the following index node if the leaf does not have enough space.
3. Step 3: Split the index node if it is too tiny and copy the center element to the following index page.

Example

In the B+ Tree of order five depicted in the accompanying image, enter the number 195.

After 190, 195 will be added to the right subtree of 120. Please put it in the appropriate place.

The node has more elements than the maximum allowed, which is 4. Thus it is divided, and the median node is placed above the parent.

Since the index node now violates the B+ tree properties by having six children and five keys, we must separate it, as indicated in the following diagram.

Deletion in B+ Tree

1. First, remove the key and information from the leaves.
2. Step 2: Merge down the leaf node with its sibling and remove the key in between them if the leaf node has fewer elements than the required number.
3. Step 3: Merge the index node with its sibling and shift the key down if the index node has fewer items than the required number.

Example

From the B+ Tree in the accompanying diagram, remove the key 200.

195 follows 200 in the right subtree of 190; remove it.

Use the numbers 195, 190, 154, and 129 to merge the two nodes.

The only element in the node currently breaking the B+ Tree's rules is element 120. As a result, we must combine it using the numbers 60, 78, 108, and 120.

The height of the B+ Tree will now be lowered by 1.

B- Tree.

We must consider the vast quantity of data that will only fit in the main memory to comprehend the utilization of B-Trees. Data is read from the disc in blocks when the number of keys is high. Reducing the number of disc accesses is the central goal of employing B-Trees. Most tree operations, such as search, insert, delete, max, min, etc., call for O(h) disc accesses, where h is the tree height. A fat tree is the B-tree. By packing as many keys as you can into each B-Tree node, the height of B-Trees is maintained to a minimum. The B-low Tree's height results in a considerable reduction in the overall number of disc visits for the majority of operations.

Time complexity in B- trees

1. The time complexity for the search algorithm is O(log n).
2. The time complexity for the insert algorithm is O(log n).
3. The time complexity for the delete algorithm is O(log n).

The total number of elements in the B-tree is denoted by "n."

B-Tree properties include:

1. The level of every leaf is the same.
2. The word minimal degree 't' is used to define the B-Tree. The size of a disc block determines the value of "t."
3. Every node, excluding the root, must have t-1 keys or more.
4. A maximum of (2*t - 1) keys may be present in any node, including the root.
5. Unlike the Binary Search Tree, the B-Tree expands and contracts from the root.
6. The time complexity to search, insert, and remove is O, similar to other balanced Binary Search Trees (log n).
7. Only at Leaf Nodes does a Node in a B-Tree get inserted.

Here is an illustration of a minimum order B-Tree. 5

Be aware that the minimum order value in real-world B-trees is substantially higher than 5.

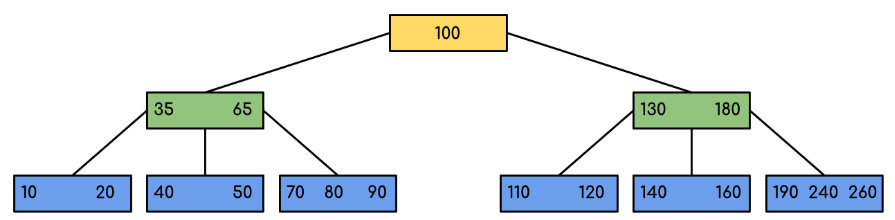
In the figure above, we can see that every leaf node is at the same level, and every non-leaf node has a key that is one less than the number of its children and no empty subtree.

Facts Worth Knowing About B-Trees

1. The B-minimum Tree's height, where n is the number of nodes, and m is the most number of offspring a node may have, is as follows:
2. The B-maximum Tree's height with n nodes and t, the smallest number of children a non-root node can have, is as follows: and

Traversal in B- Tree

Traversal is comparable to in-order binary tree traversal. Starting with the leftmost child, we recursively print that child before doing the same for the keys and remaining children.

Searching in the B-Tree.

1. Let k be the searchable key.
2. Recursively descend starting at the root.
   1. If not, the node's suitable child (the child that comes just before the first more significant key) is reached.
3. Return NULL if we reach a leaf node but can't locate k.

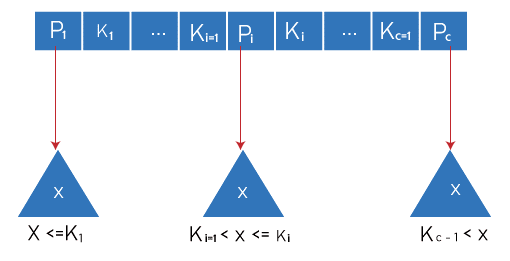
A binary tree search is comparable to a B-Tree search. The algorithm uses recursion and is identical. The search is optimized at each level so that if the key value is unavailable in the parent's range, it is in a different branch. These numbers are sometimes called limiting or separation values since they restrict the search. It will display NULL if we reach a leaf node and can't find the necessary key.

Examples

Input: In the given b- tree 120 is searched

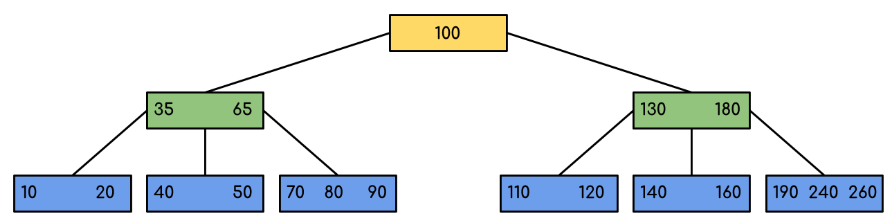
Solution:

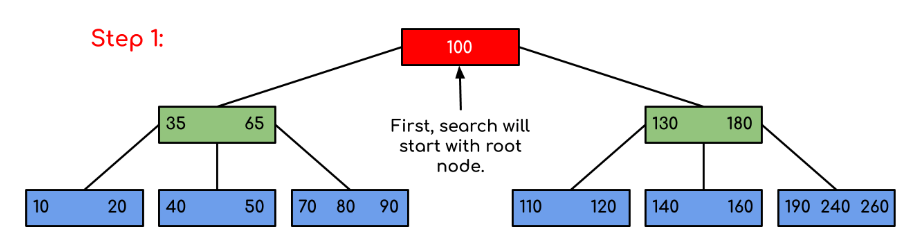
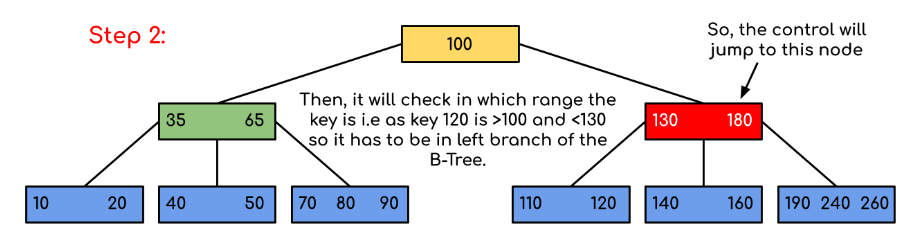
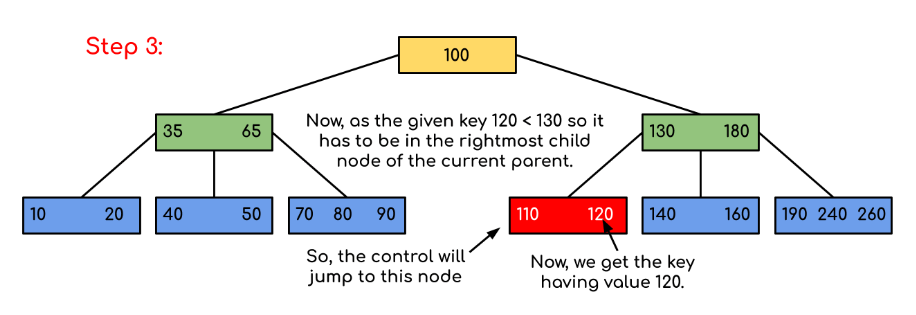
Here, our search was made more efficient by just reducing the likelihood that the key holding the value may be present. Similar to the previous example, if we had to search for 180, the control would have stopped at step 2 since the program would have discovered that the key 180 was already present in the current node. Additionally, if it needs to find 90, it will immediately move to the left subtree since 90 100, and the control flow will proceed as in the case before.

There are two conventions for defining a B-Tree: the minimum degree convention and the order convention. We have adhered to the minimal degree convention and will continue to do so in further B-Tree postings. Additionally, the program above uses the same variable names.

B-Tree applications:

1. It is employed in massive databases to access information stored on discs.
2. Using the B-Tree, searching for data in a data collection may be completed much more quickly.
3. Multilevel indexing is possible with the indexing capability, and most servers additionally employ the B-tree strategy.