Introduction to 1D-Arrays

One Dimensional Array

Technical Definitions

The simplest version of an Array is a One-Dimensional Array, in which the items are stored linearly and may be accessed individually by supplying the index value of each member in the array.

A One-Dimensional Array is a collection of objects of the same data type that are stored in a linear order under the same variable name.

One Dimensional Array in C: An Overview

In C, a one-dimensional array may be seen as a single row where the elements are stored. All of the components are stored in memory at the same time. Now we'll look at declaring, initialising, and accessing array elements:

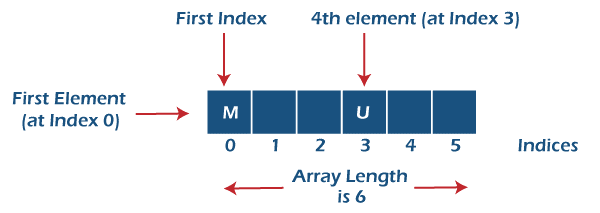
Declaration of an Array

The data type can be any type when declaring a one-dimensional array in C, and the array can be given any name, much like a random variable. Syntax:

int array[10]; //where array is the name of the integer type array, and 10 is the size of the array

Initialization of an array

All entries in static uninitialized arrays have garbage values at first, but we may explicitly initialise them at their declaration.

Syntax:

<data_type> <array_name> [array_size]={value1, value2, value3,…};

• An array's datatype is the type of its items.
• The variable name is array_name, which can be any valid identifier.
• size refers to the array's size.
• Initializers are constants like value1, value2, and so on. A comma(,) separates each value, followed by a semi-colon (;) after the closing curly brace ().
• A comma separates parameterized values from constant values.

If we explicitly initialise array items within the list at the time of declaration, we may avoid expressing the array size within square brackets. In that scenario, the size of the items list will be used as the array size.

Example:

int array[10]; //where array is the name of the integer type array, and 10 is the size of the array

If we wish to set the value of all integer array items to zero, we can simply write:

int <array name>[size] = {0};

Accessing an Array Element

Elements are accessible in one-dimensional arrays in C by supplying the array name and the index value within square brackets. The indexing of an array begins at 0 and ends at size-1. If we try to access array items outside of the range, the compiler will return a trash value rather than an error message.

Syntax:

<array_name>[index];

Example:

int numbers[5] = {0, 1, 2, 3, 4};
printf("%d", numbers[0]); //Array element at index 0 is printed
printf("%d", numbers[-1]); //Garbage value will be printed

In C, here's a programme that shows how to declare, initialise, and access elements in a one-dimensional array:

#include <stdio.h>
int main() {
int array[3] = {11, 23, 39}; //declaring and initializing one-dimensional array in C




// After declaration, we can also initialize array as:
// array[0] = 11; array[1] = 23; array[2] = 39;




for (int i = 0; i < 3; i++) {
// accessing elements of array
printf(" Value of array[%d]: %d\n", i, array[i]);
}
}

Output

Value of array[0]: 11
Value of array[1]: 23
Value of array[2]: 39

We initialised an array of size 3 and the name array in this C programming code at the time of declaration. We're trying to print the array values by accessing its elements at the conclusion of the function.

One-Dimensional Array Declarative Rules

In C, there are several rules for declaring a one-dimensional array.

• The array variable must be declared before it may be used or accessed.
• Indexing in an array begins at 0 and finishes at size-1. For example, if arr[10] has a size of 10, element indexing runs from 0 to 9.
• When declaring one-dimensional arrays in C, we must provide the data type and variable name.
• When the declaration provides array size within square brackets, we can explicitly initialise them.
• Each array element is stored in a contiguous memory area and is accessed using a unique index number.

C One-Dimensional Array Initialization

We can either initialise array items after declaration or do so directly at the time of declaration. In C, one-dimensional arrays are either populated at compile time or at run time.

Initialization at Compile Time

Static-initialization is another name for compile-time initialization. When we define the array implicitly, the array items are initialised.

Syntax:

<data_type> <array_name> [array_size] = { list of elements};

Example:

int age[5] = {27, 32, 16, 72, 4};

Compile-Time Initialization is demonstrated using a C programme:

#include <stdio.h>
int main(){
    int numbers[3]={10,9,8};
    printf(" Compile-Time Initialization Example:\n");
    printf(" %d ",numbers[0]);
    printf("%d ",numbers[1]);
    printf("%d ",numbers[2]);
}

Output

10 9 8

In this C programme code, we've created a three-dimensional array numbers with the entries 10, 9, and 8 in the list. This is compile-time initialization, and we've printed all of its values by accessing index-wise at the end.

Initialization at Runtime

Dynamic-initialization is another name for runtime initialization. After the programme has been properly compiled, the array entries are initialised during runtime.

Example:

scanf("%d", &numbers[0]); //initializing 0th index element at runtime dynamically

The following is a C programme that demonstrates Run-Time Initialization:

#include <stdio.h>




int main() {
int numbers[10];
printf("\n Example of Run-Time Initialization:\n");
printf("\n Enter the array elements: ");




for (int i = 0; i < 10; i++) {
scanf("%d", &numbers[i]);
}




printf(" Accessing array elements after dynamic Initialization: ");




for (int i = 0; i < 10; i++) {
printf("%d ", numbers[i]);
}
    
    return 0;
}

Input

Example of Run-Time Initialization:    




Enter the array elements: 100 90 80 70 60

Output

Accessing array elements after dynamic Initialization: 100 90 80 70 60

In this C programming code, we've just declared an array numbers of size 5 to show runtime initialization. Following that, we ask the user to enter the array values to initialise it when the code has been compiled. Finally, we printed the values by accessing them index-by-index.

In C, Copying One-Dimensional Arrays

If we have two arrays, first_array and second_array, one of which is initialised and the other of which is just defined, and we need to copy elements from first_array to second_array, we can't just write:

int first_array[5] = {5,4,3,2,1};
int second_array[5];
second_array = first_array; //This statement is wrong, it will produce an error

The main requirement for copying an array is that the copy array's size be smaller than the original array's.

In C, create a programme to demonstrate copying elements of a one-dimensional array.

#include <stdio.h>




int main() {
int first_array[5] = {60, 50, 40, 30, 20};
int second_array[5];
printf("Copying One-Dimensional Arrays in C:\n");
printf("First_array elements: ");




for (int i = 0; i < 5; i++) {
printf("%d ", first_array[i]);
second_array[i] = first_array[i]; // Copying first_array elements to second_array
}




printf("\nSecond_array elements after copying: ");




for (int i = 0; i < 5; i++) {
printf("%d ", second_array[i]);
}
}

Output

Copying One-Dimensional Arrays in C:
First_array elements: 10 20 30 40 50 
Second_array elements after copying: 10 20 30 40 50 

We've used two arrays in our C programming code: first_array and second_array. We are allocating first_array values to second_array within a loop to demonstrate the notion of copying array items. first_array has been initialised at the time of declaration. We've printed the values of both arrays at the end.

Points to Keep in Mind When Using an Array in C

• At C, an array is a group of comparable data-type items that are stored in the same memory region.
• All of the elements in a C array have the same data type and may be accessed using their unique index value.
• The indexing of an array begins at 0 and ends at size-1.
• In C, one-dimensional arrays can be populated statically (at build time) or dynamically (during runtime) (during runtime).
• When declaring one-dimensional arrays in C, we must specify the data type, array variable name, and array size in square brackets.

Conclusion

• In C, arrays are derived data types that contain components of the same data type.
• Indexing in one-dimensional arrays in C starts at 0 and stops at size-1, and attempting to retrieve an element outside of this range will result in a garbage value.
• When declaring one-dimensional arrays in C, we must add a data type, array variable name, and array size in square brackets.
• In C, one-dimensional arrays can be populated statically (at build time) or dynamically (during runtime) (during runtime).
• Because all of the items of an array are stored in contiguous memory regions, we may use their unique index number to retrieve them.