Queue operations in Data Structure
Queue - Queue is a linear data structure or first in first out data structure means the first element added in the queue will be removed first and the last element will be removed in last. Its behavior is defined by the values stored and operations performed on it.
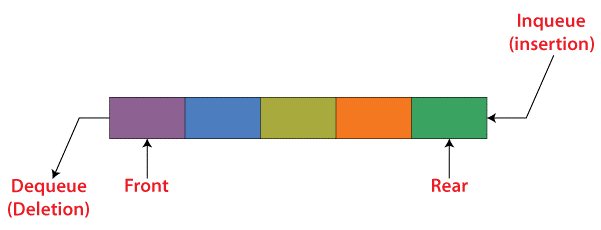
Applications of Queue Data Structure:
- Graph Traversal Algorithm (Breadth Frist Search),
- CPU Scheduling,
- Disk Scheduling, etc.
Let us see some primitive operations performed on it with examples:
- enqueue() – Enqueue method is used to insert element at end in a queue
- dequeue() – Dequeue method removes the first element of the queue
- isFull() – isFull method is used to check whether the queue is full or not
- isEmpty() – isEmpty method is used to check whether the queue is empty or not
- size() – Size method is used to find the number of elements present in the queue
- front() – Front method is used to find the first element present in the queue
C++ Code:
// C++ Program to perform operations on queue
#include <iostream>
using namespace std;
// Declaring all the operations performed on Queue
// Function of type integer will return an integer value and functions of types void will not return any value
void enqueue(int value);
void dequeue();
int isFull();
int isEmpty();
int front();
int size();
int myQueue[10]; // Creating a array of size 10 and will make it behave like queue
// n is the size of the queue and front_index and rear_index will point to front and rear element of the queue respectively
int front_index = -1, rear_index = -1, n = 10;
int main()
{
int x;
x = isEmpty(); // X will store the value returned by the isEmpty Function
// "Queue is Empty!" will be printed if x is equal to 1 or "Queue is not Empty!" will be printed if x is equal to 0
x ? cout << "Queue is Empty!" << endl : cout << "Queue is not Empty!";
// Inserting elements in the queue using the enqueue function
enqueue(30);
enqueue(44);
enqueue(90);
enqueue(53);
enqueue(12);
enqueue(99);
// Checking how many elements are there in the queue
x = size();
cout << "Number of elements in the queue is " << x << endl;
x = isFull();
// "Queue is Full!" will be printed if x is equal to 1 or "Queue is not Full!" will be printed if x is equal to 0
x ? cout << "Queue is Full!" << endl : cout << "Queue is not Full!" << endl;
x = isEmpty();
// "Queue is Empty!" will be printed if x is equal to 1 or "Queue is not Empty!" will be printed if x is equal to 0
x ? cout << "Queue is Empty!" << endl : cout << "Queue is not Empty!" << endl;
x = front();
// The first statement of the below ternary operator will be executed if the x is not equal to 0
x ? cout << "Front element of the queue = " << x << endl : cout << "No front element. The queue is empty!" << endl;
// Deleting and printing all the elements of the queue using the dequeue function
cout << "Elements of queue are: ";
do
{
dequeue();
} while (front_index != -1);
cout << endl;
// After deleting all the value from the queue, trying to print front element.
x = front();
x ? cout << "Front element of the queue = " << x << endl : cout << "No front element. The queue is empty!" << endl;
}
// Function to insert element in the queue
void enqueue(int value)
{
if (rear_index == n - 1) // Condition to check whether the queue is Full or not
{
cout << "Overflow!" << endl;
return;
}
if (front_index == -1)
{
front_index = 0;
rear_index = 0;
}
else
{
rear_index = rear_index + 1;
}
myQueue[rear_index] = value; // Adding the value after increasing the rear_index by 1
}
// Function to delete elements from the Queue. Actually, we not delete the elements but we just forget those elements
void dequeue()
{
int deleted_ele;
if (front_index == -1) // Condition to check whether the queue is empty or not
{
cout << "Underflow!";
return;
}
deleted_ele = myQueue[front_index]; // Storing the value of the front element of the queue
cout << deleted_ele << " ";
/*In the below statements we are increasing the front_index by 1 and if we are deleting the last element,
we are making rear_index and front_index equal to -1 */
if (front_index == rear_index)
{
front_index = -1;
rear_index = -1;
}
else
{
front_index++;
}
}
// Function to check whether the Queue if Full or not
int isFull()
{
// The function will return 1 if the queue is full otherwise it will return 0
if (front_index == 0 && rear_index == n - 1) // Condition of FULL queue
{
return 1;
}
return 0;
}
// function to check whether the queue is empty or not
int isEmpty()
{
// The function will return 1 if the queue is empty otherwise it will return 0
if (front_index == -1) // Condition of empty queue
{
return 1;
}
return 0;
}
// Function to find the number of elements in the queue
int size()
{
if (front_index == -1) // It will return zero if the queue is empty
{
return 0;
}
return rear_index - front_index + 1; // It will return the number of elements present in the list
}
// Function to print the front element
int front()
{
// It will return 0 when the queue is empty otherwise the front element
if (front_index == -1)
{
return 0;
}
return myQueue[front_index];
}
The output of the above Program:
Queue is Empty!
Number of elements in the queue is 6
Queue is not Full!
Queue is not Empty!
Front element of the queue = 30
Elements of queue are: 30 44 90 53 12 99
No front element. The queue is empty!
C Code:
// C program to implement the queue operations
#include <stdio.h>
/* Declaring the operations performed on the Queue. The functions of type int will return an integer value and functions of type
void will not return any value. */
void enqueue(int value);
void dequeue();
int isFull();
int isEmpty();
int front_ele();
int size();
int myQueue[10]; // Declaring the queue of size 10
// n is the size of the queue and front and rear will point to front and rear element of the queue respectively
int front = -1, rear = -1, n = 10;
int main()
{
int x;
x = isEmpty(); // X will store the value returned by the isEmpty Function
// "Queue is Empty!" will be printed if x is equal to 1 or "Queue is not Empty!" will be printed if x is equal to 0
x ? printf("Queue is Empty!\n") : printf("Queue is not Empty!\n");
// Inserting elements in the queue using the enqueue function
enqueue(13);
enqueue(22);
enqueue(99);
enqueue(35);
enqueue(124);
enqueue(11);
// Checking how many elements are there in the queue
x = size();
printf("The number of elements present in the queue = %d\n", x);
x = isFull();
// "Queue is Full!" will be printed if x is equal to 1 or "Queue is not Full!" will be printed if x is equal to 0
x ? printf("Queue is Full!\n") : printf("Queue is not Full!\n");
x = isEmpty();
// "Queue is Empty!" will be printed if x is equal to 1 or "Queue is not Empty!" will be printed if x is equal to 0
x ? printf("Queue is Empty!\n") : printf("Queue is not Empty!\n");
x = front_ele();
// The first statement of the below ternary operator will be executed if the x is not equal to 0
x ? printf("Front element of the queue = %d\n", x) : printf("No front element. The queue is empty!\n");
// Deleting and printing all the elements of the queue using the dequeue function
printf("Elements of queue are: ");
do
{
dequeue();
} while (front != -1);
printf("\n");
// After deleting all the value from the queue, trying to print front element.
x = front_ele();
x ? printf("Front element of the queue = %d\n", x) : printf("No front element. The queue is empty!\n");
}
// Function to insert element in the queue
void enqueue(int value)
{
if (rear == n - 1) // Condition to check whether the queue is Full or not
{
printf("Overflow!\n");
return;
}
if (front == -1)
{
front = 0;
rear = 0;
}
else
{
rear = rear + 1;
}
myQueue[rear] = value; // Adding the value after increasing the rear_index by 1
}
// Function to delete element from the queue
void dequeue()
{
int deleted_ele;
if (front == -1) // Condition to check whether the queue is empty or not
{
printf("Underflow\n");
return;
}
deleted_ele = myQueue[front]; // Storing the value of the front element of the queue
printf("%d ", deleted_ele);
/*In the below statements we are increasing the front_index by 1 and if we are deleting the last element,
we are making rear_index and front_index equal to -1 */
if (front == rear)
{
front = -1;
rear = -1;
}
else
{
front++;
}
}
// Function to check whether the Queue if Full or not
int isFull()
{
// The function will return 1 if the queue is full otherwise it will return 0
if (front == 0 && rear == n - 1) // Condition of FULL queue
{
return 1;
}
return 0;
}
// function to check whether the queue is empty or not
int isEmpty()
{
// The function will return 1 if the queue is empty otherwise it will return 0
if (front == -1) // Condition of empty queue
{
return 1;
}
return 0;
}
// Function to find the number of elements in the queue
int size()
{
if (front == -1) // It will return zero if the queue is empty
{
return 0;
}
return rear - front + 1; // It will return the number of elements present in the list
}
// Function to print the front element
int front_ele()
{
// It will return 0 when the queue is empty otherwise the front element
if (front == -1)
{
return 0;
}
return myQueue[front];
}
The output of the above program:
Queue is Empty!
The number of elements present in the queue = 6
Queue is not Full!
Queue is not Empty!
Front element of the queue = 13
Elements of queue are: 13 22 99 35 124 11
No front element. The queue is empty!