Tree terminology in Data structures
Data structures
The storage used to organize and store data is known as a data structure, and it is a method where data can be arranged on a computer to be updated or accessed proficiently. A data model is a database used to store and manage data and is a system for optimizing and managing computer resources. Data structures are not just for storing data. Almost every program or application has a basic and advanced data structure. We have many basic and advanced types of data structures, and it is hard to find a program without data structures in any programming language.
Data structures are forms used to store, process, organize and retrieve data proficiently and quickly in a specific format on a machine or computer. Data structures help render data for easy use and handling of information. Any program foundation, software, or application consists of two components: data and algorithms—the communication of information and the rules and regulations of the algorithm that turn information into action.
We can depict all the above in the following two simple equations:
Operations that are permissible on the data + Related data = Data Structure
Algorithms + Data structures = Programs
There are two types of data structures:
- Linear Data structures
- Non-linear data structures
Linear Data structures
This type of data structure adds information to the data model. Each element is related to the component before and after. So, you can remove the instance. There are four types of this data structure. They are:
- Queue
- Stack
- Linked lists
- Array
Non-linear Data structures
A data structure in which data elements are organized in different ways. Content is not a series of data presented at different levels. There are several ways to move directly from one element to another. Unauthorized data points are shared at least once. There are two types of this non-linear data structure. They are:
- Tree data structure
- Graph data structure
Tree Data structure
A tree is a hierarchical and non-linear data structure with nodes. Each node in the Tree contains a message value and stores the name passed to another ("child") node.
Organizing these files is a great way to collect your information and make it easy to reference on your computer. The tree data structure consists of sub-nodes, structural nodes, and a central node connected by the edges, and this data structure also has leaves, branches, and roots attached.
The data in the Tree is plotted so that it is not linear. But they are organized differently, or we can say hierarchically. The trees are considered non-linear as they are hierarchical.
Tree data structures differ from queues, stacks, arrays, and linked lists. A tree is a hierarchical structure; data structures have nodes representing and supporting the process. Asynchronous Data Warehouse Tree types collect different levels of information together in a data structure called a root node. All data types are stored in the root location. Each line has a message. We call the branches of the data structure at the bottom of the Tree.
There is a particular type of Tree called the Binary tree. It is used for the same data storage purposes and is a unique data structure. This data structure is a particular tree as it can have only a maximum number of two children, i.e., a binary tree can either have 0, 1, or 2 children at any stage. This allows the binary Tree to provide the benefits of an ordinary linked list and array, making searching an element stored easy (as they are sorted data structures). A binary search tree can perform the deletion and insertion of elements competing with the speed of linked lists.
Tree terminology in data structures
Before understanding any concept, we must be familiar with the language usually used in the topic. The tree concept of data structures uses pretty simple and straightforward terminology. Hence, below are the basic terminology traditionally used in the tree data structure concept.
- Node
- Root
- Edge
- Parent
- Child
- Siblings
- Neighbour node
- Leaf
- Internal nodes
- External nodes
- Ancestors
- Descendants
- Degree
- Level
- Height
- Depth
- Path
- Subtree
Node
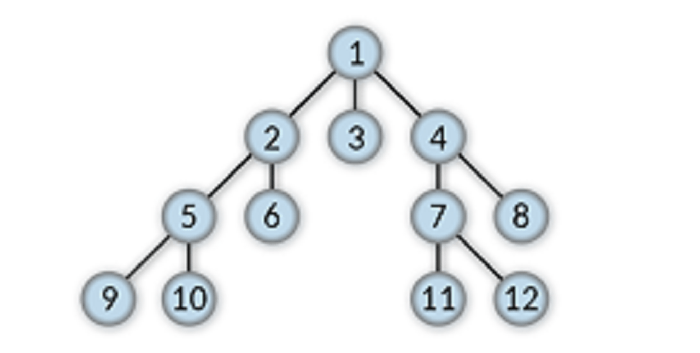
The entities, values, or keys stored in a tree data structure are known as Nodes. It is, in fact, the place where we place our information or data in a tree data structure.
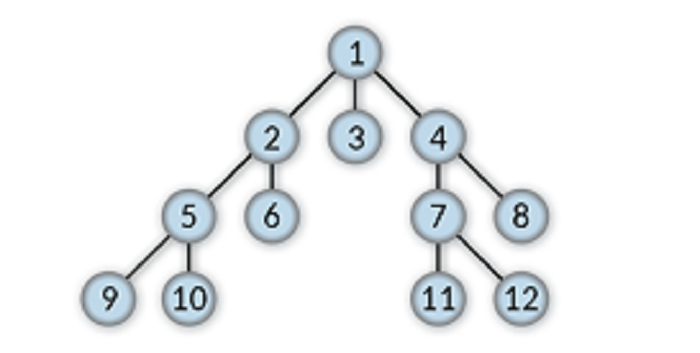
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, and 12 are the nodes in the above Tree.
Edge
An edge is a connection among given consecutive nodes in a tree data structure. The nodes and edges together make a tree data structure. Nodes and edges are the only two factors that can be found in any tree data structure. We can say that without these two, a data structure cannot be treated as a tree. Edges are represented by straight lines connecting two nodes.
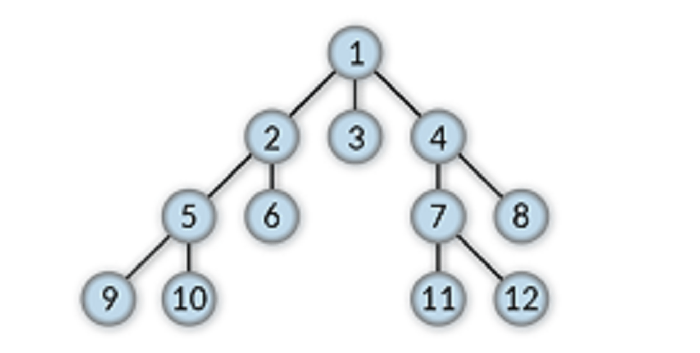
The black lines in the above Tree are its edges.
Root Node
The node that lies at the peak of the tree data structure is known as the root node. The root node only has child nodes, and it does not have any parent nodes. The formation of a tree data structure starts from the root node, and any tree data structure has only one root node. That data structure cannot be treated as a tree if there is more than one root node.
The root node in the above tree is 1.
Parent Node
The node above any node in a tree data structure is treated as its parent node. Any node in a tree data structure can have only one parent node.
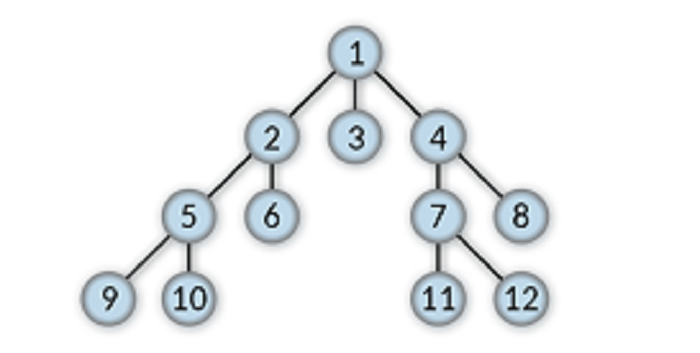
For example, 2 is the parent node of 5 and 6.
Child node
The node below any given node in a tree data structure is treated as its parent node. Any node in a tree data structure can have any number of child nodes, and leaf nodes do not have child nodes. A child node may or may not have further child nodes but must have a parent node. If any node in a tree data structure does not have a parent node, then it cannot be treated as a child node.
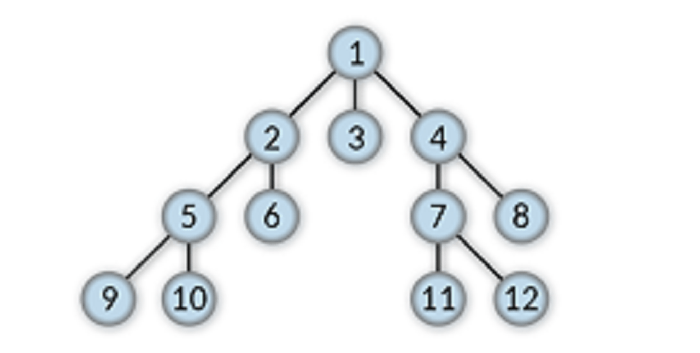
For example, 7 and 8 are the child nodes of 4.
Siblings
Child nodes of one parent node are called sibling nodes. As the name suggests, sibling nodes share a single parent.
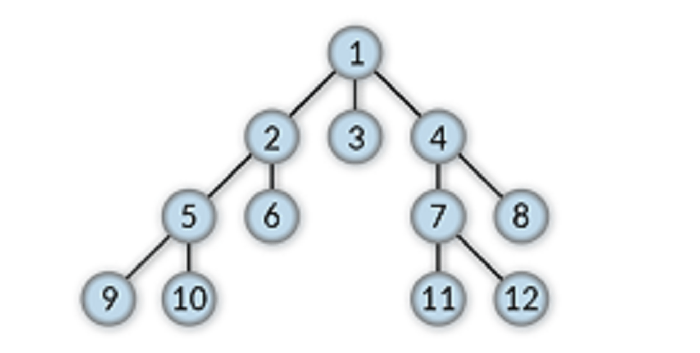
For example, 9 and 10 are sibling nodes.
Neighbour node
Any two nodes directly connected by a single edge are called neighbour nodes. For any given node in a tree data structure, its respective parent node and child nodes can be treated as neighbour nodes.
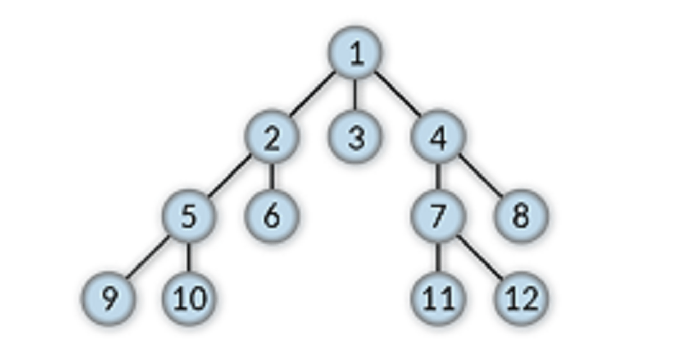
For example, 2, 9, and 10 are the neighbour nodes of 5.
Leaf node
The nodes that do not have child nodes are called leaf nodes or terminal nodes, and they put an end to their respective branch of the tree data structure.
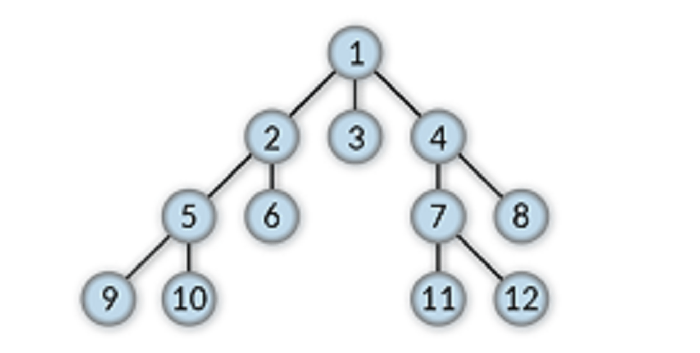
9, 10, 6, 3, 11, 12, and 8 are the leaf nodes.
Internal nodes
All the nodes in a tree data structure, excluding the root and leaf nodes, are treated as internal nodes.
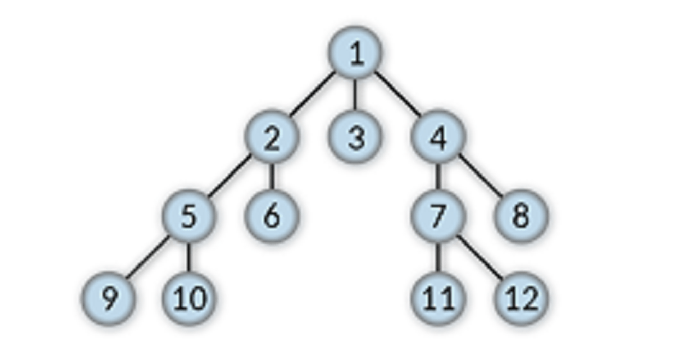
2, 4, 5, and 7 are the internal nodes.
External nodes
All the leaf nodes and root nodes in a given tree data structure are called external nodes.
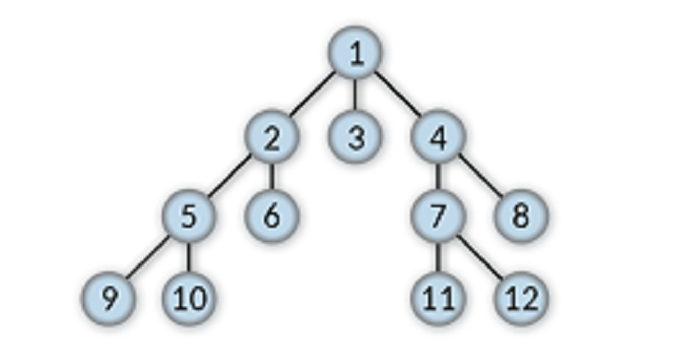
1, 9, 10, 6, 3, 11, 12, and 8 are the external nodes.
Ancestors
All the nodes that precede a given node in a tree data structure are treated as ancestor nodes to that node.
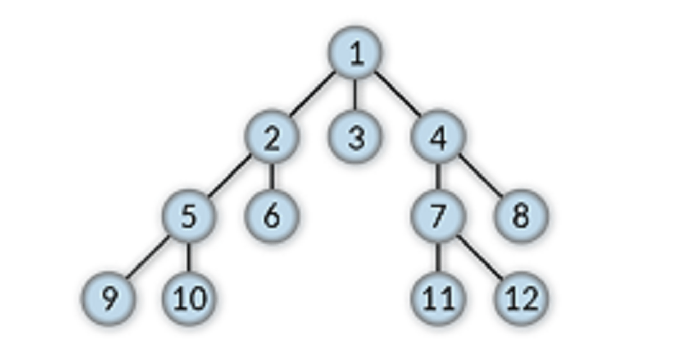
For example, 5, 2, and 1 are the ancestors of 10.
Descendants
All the nodes that lie below a given node in a tree data structure are treated as the descendant nodes of that node.
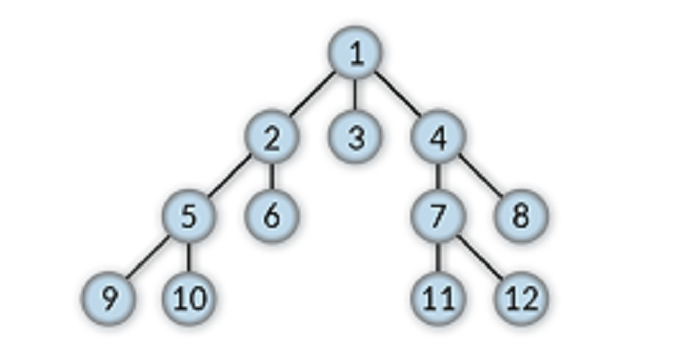
For example, 7, 8, 11, and 12 are the descendants of 4.
Degree
The number of child nodes of a given node in a tree data structure is called the Degree of that node. The Degree of the node with the highest Degree among all other degrees in a given tree data structure is treated as the Degree of the Tree.
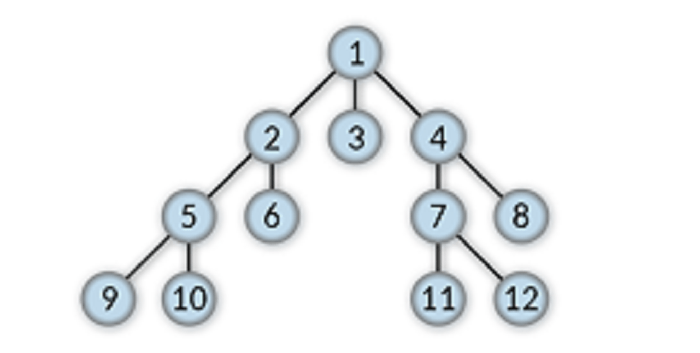
For example, a degree of 7 is 2.
Level
The level of a given node in a tree data structure is the number of edges that connect it to the root node. Root node's child nodes have a level equal to 1; their child nodes have a level equivalent to 2.
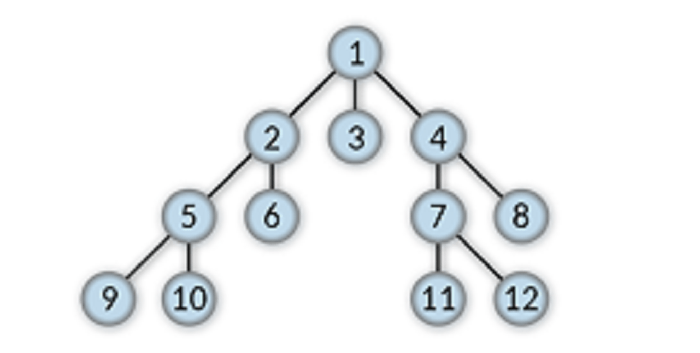
For example, a level of 6 is 2.
Height
In a tree data structure, the level of a node is calculated starting from the root node, while its height is calculated starting from leaf nodes. The height of any leaf node in a tree data structure is equal to zero.
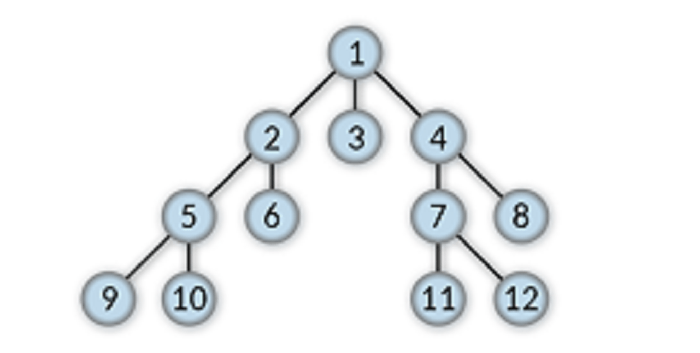
For example, the height of 4 is 2.
Depth
The depth of a given node in a tree data structure is the number of edges that connect it to the root node. The largest tree data structure's largest depth is treated as that Tree's depth. The largest depth is equal to the depth of the leaf node with the longest path from the root node.
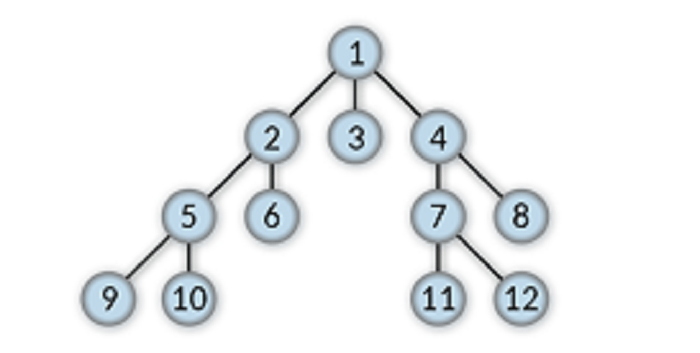
For example, a depth of 5 is 2.
Path
The sequence of edges and nodes between any two selected nodes in a tree data structure is called the path between the given nodes. We can only have a single path between two nodes in a tree data structure.
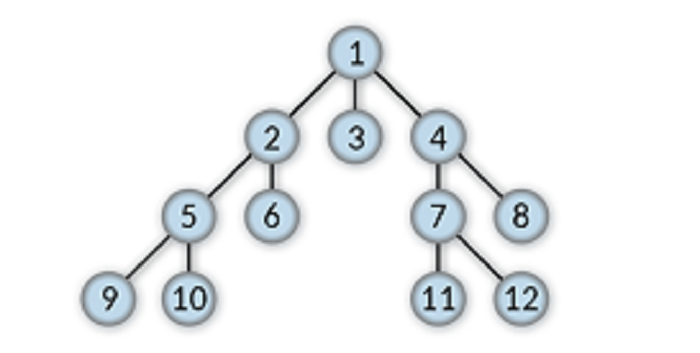
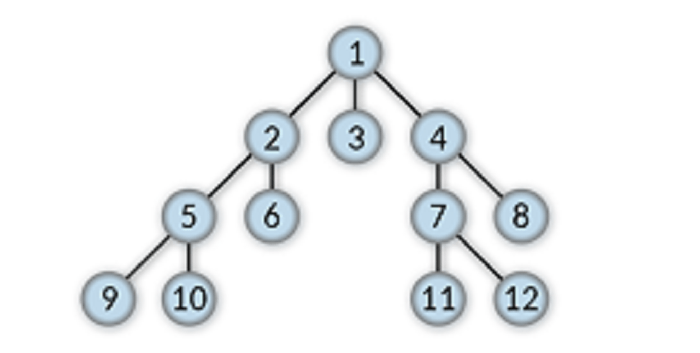
For example, the path between 6 and 7 is
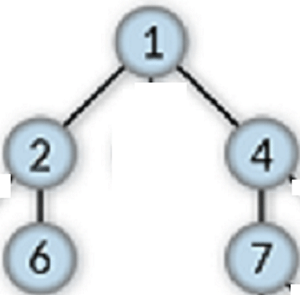
Subtree
Any node under the root node, along with its chosen descendants, is known as a subtree.
An example of a subtree for the above tree is