Binary Search Tree

Binary Search Tree: A binary search tree is a type of tree in which every node is organized in the sorted order. It is also called an ordered binary tree.

Properties of BST

1. The left sub-tree value is less than the root node.
2. Similarly, the right sub-tree value is higher than the root node.
3. This rule is reapplied to all left and right sub-trees of the root.

Operations of the BST

There are three types of operations in the BST.

1. Search operation
2. Insertion operation
3. Delete operation

Search operation:

The search operation is used to search a particular node in a BST. Whenever any node in BST is searched, that node is first compared with the root node. If the node is less than the root node, it is searched in the left subtree. If the node is greater than the root node, it is searched in the correct subtree.

Algorithm of the Search operation

struct node* search(int data)
{    
struct node *current = root;   
 printf("Visiting elements: ");                
while(current->data != data)
{           
 if(current != NULL) 
 { 
 printf("%d ",current->data);  
 }   
     //go to left tree                  
 if(current->data > data) 
          { 
             current = current->leftChild;
           } 
       //else go to right tree   
   Else  
  {      
  current = current->rightChild;   
 }          
 if(current == NULL){  
  return NULL;     
 }   
 }    
    }    
   return current;
 }

Insertion Operation

It is used to add a new node to a particular location in a specific situation. Whenever a new node is inserted in the BST, the location of that node is first searched. The new node is first compared with the root node. If the new node is less than the root node, search the null location in the left subtree and insert that node. If the node is greater than the root node, search the null location in the right subtree and insert that node.

Algorithm of the Insertion operation

TreeNode insert (int data, TreeNode T) 
{         
if T is NULL     
      {   
                T = (TreeNode *)malloc(sizeof (Struct TreeNode));         
          (Allocate Memory of new node and load the data into it)               
    T ? data = data;                   T ? left   = NULL;                   T ? right = NULL;           }                  
  else if T is less than T ? left     
      {              
    T ? left = insert(data, T ? left);    
               (Then node needs to be inserted in the left sub-tree. So, 
                  recursively traverse left sub-tree to find the place         
          where the new node needs to be inserted)     
      }           
     else if T is greater than T ? right    
       {                
    T ? right = insert(data, T ? right);     
               (Then node needs to be inserted in right sub-tree     
               So, recursively traverse right sub-tree to find the               
     place where the new node needs to be inserted.)    
      }    
      return T; 
}

Delete operation

This operation is used to delete a node in a specific situation. A node can be deleted from the following locations.

1. Leaf node
2. One child node
3. Two child nodes

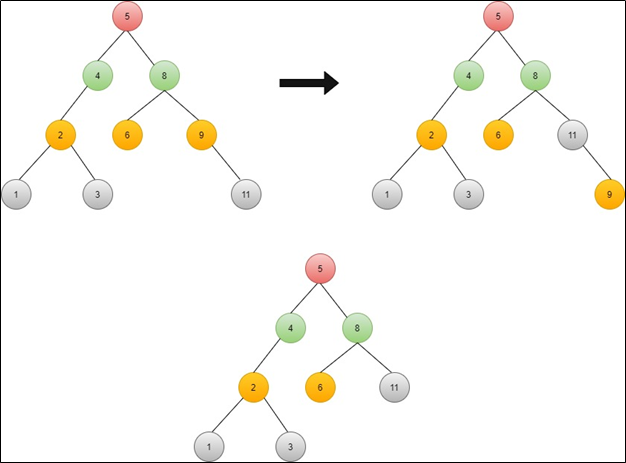
Leaf node: In this case, it simply removes the leaf node in the tree. This case is much simpler than other cases.

For example, remove the 6 in this BST.

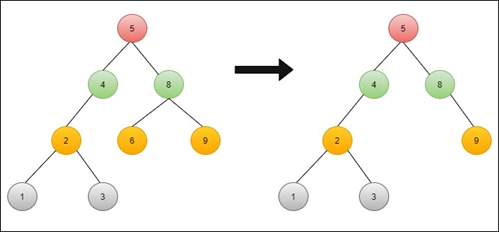
One child node: In this case, first, the original node is replaced with the child node, and then the node is removed. For example, remove the 9 in this BST.