B+ Tree in Data Structure

A B-Tree extension called B+ Tree, which enables effective search, insertion, and deletion operations.

Both Records and keys can be stored in internal and leaf nodes in a B tree. Contrarily, records (data) can only be kept on leaf nodes in a B+ tree, while inside nodes can only hold key values.

To improve the effectiveness of search queries, the leaf nodes of a B+ tree are linked together as singly linked lists.

The enormous amount of data that cannot be kept in the main memory is saved in B+ Trees. The internal nodes (keys to access records) of the B+ tree are saved in the main memory, while leaf nodes are kept in the secondary memory due to the constant size restriction of the main memory.

B-tree and B+ trees are typically used to achieve dynamic multilevel indexing. However, the disadvantage of the B-tree used for indexing is that it also keeps the data pointer (a pointer to the disc file block containing the key value), corresponding to a certain key value, in the B-tree node. This method significantly decreases the number of items that can fit inside a B-tree node, which leads to an increase in the B-level tree's structure and longer search times for records. By only storing data pointers at the tree's leaf nodes, the B+ tree gets rid of the aforementioned flaw. As a result, the interior nodes of the B tree and the leaf nodes of a B+ tree have very distinct structures. It should be emphasized that since data pointers are only present at leaf nodes, all key values and their accompanying data pointers to the disc file block must be stored by leaf nodes in order for them to be accessible. Additionally, the leaf nodes are connected to offer organized access to the records. Therefore, the leaf nodes constitute the index's first level, with the internal nodes being the other levels in a multilevel index. To only serve as a conduit for controlling the leaf nodes' key values, some of them also appear in the internal nodes.

It just acts as a medium to control the search for recordings. From the above discussion, unlike B-trees, B+-trees have two orderings, 'a' and 'b', one for internal nodes and one for external (leaf) nodes.

The structure of the internal nodes of a B+ tree of order 'a'

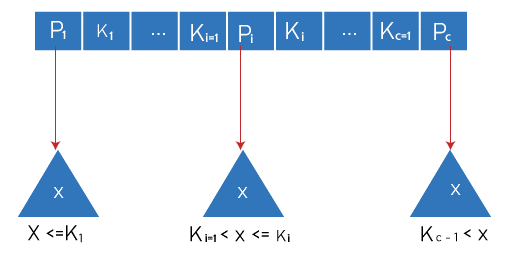
Each internal node has the format:

• where c <= a, each Pi is a tree pointer (i.e. points to another node in the tree) and each Ki is a key value.
• Each internal node has:
  K1< K2< …. < Kc-1
• For each search field value 'X' in the subtree pointed to or by Pi, the following conditions hold:
  if Ki-1 < X <= Ki, 1 < i < c and Ki-1 <; X, i = c
• Each interior node has at most "a" tree pointers.
• The root node has at least two tree pointers, and the other internal nodes each have at least \ceil(a/2) tree pointers.
• If an interior node has a 'c' pointer (c <= a), it has a 'c - 1' key value.

Advantages of B+ Trees

• Recordings can be recalled with the same number of disk accesses.
• The height of the tree remains balanced and is lower compared to the B tree.
• Data stored in a B+ tree can be accessed sequentially and directly.
• Keys are used for indexing.
• Searches are faster because data is stored only in leaf nodes.

Negative aspects of B+ Tree:

The difficulty of accessing the keys in a sequential manner is the main disadvantage of B-tree. Rapid sequential access is also possible while maintaining rapid random access in the B+ tree.

Application of a B+ tree:

• Indexing at multiple levels
• Faster tree operations (insert, delete, search)
• Database indexing

Insertion into the B+ Tree

Step 1:
Paste the new node as a leaf node

Step 2:
If the leaf does not have the required space, split the node and copy the intermediate node to the next index node.

Step 3:
If the index node does not have the required space, split the node and copy the intermediate elements to the next index page.

Deletion in B+ Tree

Step 1:
Clear keys and data from the sheet.

Step 2:
If the leaf node contains fewer than the minimum number of elements, merge the node with its siblings and remove the key between them.

Step 3:
If the index node contains fewer than the minimum number of elements, merge the node with its siblings and move the key down between them.