Lowest common ancestor in a binary search tree

Suppose you have given two values of nodes in a binary search tree. You have to find out the lowest common ancestor between the nodes.

Let’s take an example tree-

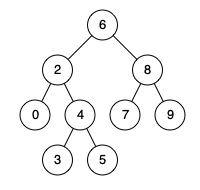
For the above binary search tree, if we take inputs 3 and 5, then the output will be 4. It is supposed that there will be a particular output for every input.

Input- 0, 4

Output- 2

Explanation- 0 and 4 both nodes are in the lower level of 2. 2 is the closest node of both nodes, so it is the lowest common ancestor.

Note: -

What is the lowest common ancestor in a binary search tree?

According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes m and n as the lowest node in T that has both m and n as descendants (where we allow a node to be a descendant of itself ).”

Algorithm:-

Step 1: Start

Step 2: Two values are taken from the user

Step 3: A tree is created

Step 4: A recursive function called. This function takes two input values and one tree node.

Step 5: If the values are less than the node value, the function is again called with the left node.

Step 6: If the values are greater than the node value, the function is called with the right node.

Step 7: If steps 5 and 6 are not satisfying, then the node value will be returned.

Step 8: The returned value will be printed.

Step 9: Stop.

Explanation of Algorithm: We take the above-given tree, and inputs are 0 and 5. If we call the recursive function with the root node and values, then the function is again called with the node's left node because 0 and 5 are both less than 6. After that, values are compared with node's value two, and here we get our answer because 0 is less than 2, but 5 is greater than 2. The function will return 2.

Code

#include <bits/stdc++.h>
using namespace std;
class node
{
	public:
	int value;
	node* left, *right;
};
/* Function to find LCA of m and n.
The function assumes that both
m and n are present in BST */
node *fun(node* root, int m, int n)
{
	if (root == NULL) 
                return NULL;
	// If both m and n are smaller
	// than root, then LCA lies in left
	if (root->value > m && root->value > n)
		return fun(root->left, m, n);
	// If both m and n are greater than
	// root, then LCA lies in right
	if (root->value < m && root->value < n)
		return fun(root->right, n1, n2);
	return root;
}
/* Helper function that allocates
a new node with the given data.*/
node* insert(int data)
{
	node* root = new node();
	root->value = data;
	root->left = root->right = NULL;
	return(root);
}
/* Driver code*/
int main()
{
	// Let us construct the BST
	// shown in the above figure
	node *root = insert(6);
	root->left = insert(2);
	root->right = insert(8);
	root->left->left = insert(0);
	root->left->right = insert(4);
            root->right->left = insert(7);
	root->right->right = insert(9);
	root->left->right->left = insert(3);
	root->left->right->right = insert(5);
	int m = 0, n = 4;
	node *t = fun(root, m, n);
	cout << "LCA of " << m << " and " << n << " is " << t->value<<endl;
	m = 4, n = 7;
	t = fun(root, n1, n2);
	cout<<"LCA of " << m << " and " << n << " is " << t->value << endl;
	m = 0, n = 2;
	t = fun(root, m, n);
	cout << "LCA of " << m << " and " << n << " is " << t->value << endl;
	return 0;
}

Output

LCA of 0 and 4 is 2
LCA of 4 and 7 is 6
LCA of 0 and 2 is 2

Complexity Analysis

Time complexity- Here, the recursion continues till we find the LCA. So, the complexity directly depends on the height of the tree. Complexity will be O(h).

Space complexity- In this recursive solution, we use constant memory. So, space complexity will be O(1).

Note- The above code and algorithm are based on a recursive approach. The main drawback of this solution is for recursion purposes, and we have to allocate the memory of the function stack. But if we use an iterative approach, then we can avoid this problem. In the iterative solution, we will use the loop in the main function. The loop will continue till we get the answer. The root is updated in every iteration by the left node or right node according to steps 5, 6, and 7 of the algorithm.