Data Structures Tutorial

Data Structures Tutorial Asymptotic Notation Structure and Union Array Data Structure Linked list Data Structure Type of Linked list Advantages and Disadvantages of linked list Queue Data Structure Implementation of Queue Stack Data Structure Implementation of Stack Sorting Insertion sort Quick sort Selection sort Heap sort Merge sort Bucket sort Count sort Radix sort Shell sort Tree Traversal of the binary tree Binary search tree Graph Spanning tree Linear Search Binary Search Hashing Collision Resolution Techniques

Misc Topic:

Priority Queue in Data Structure Deque in Data Structure Difference Between Linear And Non Linear Data Structures Queue Operations In Data Structure About Data Structures Data Structures Algorithms Types of Data Structures Big O Notations Introduction to Arrays Introduction to 1D-Arrays Operations on 1D-Arrays Introduction to 2D-Arrays Operations on 2D-Arrays Strings in Data Structures String Operations Application of 2D array Bubble Sort Insertion Sort Sorting Algorithms What is DFS Algorithm What Is Graph Data Structure What is the difference between Tree and Graph What is the difference between DFS and BFS Bucket Sort Dijkstra’s vs Bellman-Ford Algorithm Linear Queue Data Structure in C Stack Using Array Stack Using Linked List Recursion in Fibonacci Stack vs Array What is Skewed Binary Tree Primitive Data Structure in C Dynamic memory allocation of structure in C Application of Stack in Data Structures Binary Tree in Data Structures Heap Data Structure Recursion - Factorial and Fibonacci What is B tree what is B+ tree Huffman tree in Data Structures Insertion Sort vs Bubble Sort Adding one to the number represented an array of digits Bitwise Operators and their Important Tricks Blowfish algorithm Bubble Sort vs Selection Sort Hashing and its Applications Heap Sort vs Merge Sort Insertion Sort vs Selection Sort Merge Conflicts and ways to handle them Difference between Stack and Queue AVL tree in data structure c++ Bubble sort algorithm using Javascript Buffer overflow attack with examples Find out the area between two concentric circles Lowest common ancestor in a binary search tree Number of visible boxes putting one inside another Program to calculate the area of the circumcircle of an equilateral triangle Red-black Tree in Data Structures Strictly binary tree in Data Structures 2-3 Trees and Basic Operations on them Asynchronous advantage actor-critic (A3C) Algorithm Bubble Sort vs Heap Sort Digital Search Tree in Data Structures Minimum Spanning Tree Permutation Sort or Bogo Sort Quick Sort vs Merge Sort Boruvkas algorithm Bubble Sort vs Quick Sort Common Operations on various Data Structures Detect and Remove Loop in a Linked List How to Start Learning DSA Print kth least significant bit number Why is Binary Heap Preferred over BST for Priority Queue Bin Packing Problem Binary Tree Inorder Traversal Burning binary tree Equal Sum What is a Threaded Binary Tree? What is a full Binary Tree? Bubble Sort vs Merge Sort B+ Tree Program in Q language Deletion Operation from A B Tree Deletion Operation of the binary search tree in C++ language Does Overloading Work with Inheritance Balanced Binary Tree Binary tree deletion Binary tree insertion Cocktail Sort Comb Sort FIFO approach Operations of B Tree in C++ Language Recaman’s Sequence Tim Sort Understanding Data Processing Applications of trees in data structures Binary Tree Implementation Using Arrays Convert a Binary Tree into a Binary Search Tree Create a binary search tree Horizontal and Vertical Scaling Invert binary tree LCA of binary tree Linked List Representation of Binary Tree Optimal binary search tree in DSA Serialize and Deserialize a Binary Tree Tree terminology in Data structures Vertical Order Traversal of Binary Tree What is a Height-Balanced Tree in Data Structure Convert binary tree to a doubly linked list Fundamental of Algorithms Introduction and Implementation of Bloom Filter Optimal binary search tree using dynamic programming Right side view of binary tree Symmetric binary tree Trim a binary search tree What is a Sparse Matrix in Data Structure What is a Tree in Terms of a Graph What is the Use of Segment Trees in Data Structure What Should We Learn First Trees or Graphs in Data Structures All About Minimum Cost Spanning Trees in Data Structure Convert Binary Tree into a Threaded Binary Tree Difference between Structured and Object-Oriented Analysis FLEX (Fast Lexical Analyzer Generator) Object-Oriented Analysis and Design Sum of Nodes in a Binary Tree What are the types of Trees in Data Structure What is a 2-3 Tree in Data Structure What is a Spanning Tree in Data Structure What is an AVL Tree in Data Structure Given a Binary Tree, Check if it's balanced B Tree in Data Structure Convert Sorted List to Binary Search Tree Flattening a Linked List Given a Perfect Binary Tree, Reverse Alternate Levels Left View of Binary Tree What are Forest Trees in Data Structure Compare Balanced Binary Tree and Complete Binary Tree Diameter of a Binary Tree Given a Binary Tree Check the Zig Zag Traversal Given a Binary Tree Print the Shortest Path Given a Binary Tree Return All Root To Leaf Paths Given a Binary Tree Swap Nodes at K Height Given a Binary Tree Find Its Minimum Depth Given a Binary Tree Print the Pre Order Traversal in Recursive Given a Generate all Structurally Unique Binary Search Trees Perfect Binary Tree Threaded Binary Trees Function to Create a Copy of Binary Search Tree Function to Delete a Leaf Node from a Binary Tree Function to Insert a Node in a Binary Search Tree Given Two Binary Trees, Check if it is Symmetric A Full Binary Tree with n Nodes Applications of Different Linked Lists in Data Structure B+ Tree in Data Structure Construction of B tree in Data Structure Difference between B-tree and Binary Tree Finding Rank in a Binary Search Tree Finding the Maximum Element in a Binary Tree Finding the Minimum and Maximum Value of a Binary Tree Finding the Sum of All Paths in a Binary Tree Time Complexity of Selection Sort in Data Structure How to get Better in Data Structures and Algorithms Binary Tree Leaf Nodes Classification of Data Structure Difference between Static and Dynamic Data Structure Find the Union and Intersection of the Binary Search Tree Find the Vertical Next in a Binary Tree Finding a Deadlock in a Binary Search Tree Finding all Node of k Distance in a Binary Tree Finding Diagonal Sum in a Binary Tree Finding Diagonal Traversal of The Binary Tree Finding In-Order Successor Binary Tree Finding the gcd of Each Sibling of the Binary Tree Greedy Algorithm in Data Structure How to Calculate Space Complexity in Data Structure How to find missing numbers in an Array Kth Ancestor Node of Binary Tree Minimum Depth Binary Tree Mirror Binary Tree in Data Structure Red-Black Tree Insertion Binary Tree to Mirror Image in Data Structure Calculating the Height of a Binary Search Tree in Data Structure Characteristics of Binary Tree in Data Structure Create a Complete Binary Tree from its Linked List Field in Tree Data Structure Find a Specified Element in a binary Search Tree Find Descendant in Tree Data Structure Find Siblings in a Binary Tree Given as an Array Find the Height of a Node in a Binary Tree Find the Second-Largest Element in a Binary Tree Find the Successor Predecessor of a Binary Search Tree Forest of a Tree in Data Structure In Order Traversal of Threaded Binary Tree Introduction to Huffman Coding Limitations of a Binary Search Tree Link State Routing Algorithm in Data Structure Map Reduce Algorithm for Binary Search Tree in Data Structure Non-Binary Tree in Data Structure Quadratic Probing Example in Hashing Scope and Lifetime of Variables in Data Structure Separate Chaining in Data Structure What is Dynamic Data Structure Separate Chaining vs Open Addressing Time and Space Complexity of Linear Data Structures Abstract Data Types in Data Structures Binary Tree to Single Linked List Count the Number of Nodes in the Binary Tree Count Total No. of Ancestors in a Binary Search Tree Elements of Dynamic Programming in Data Structures Find cost of tree with prims algorithm in data structures Find Preorder Successor in a Threaded Binary Tree Find Prime Nodes Sum Count in Non-Binary Tree Find the Right Sibling of a Binary Tree with Parent Pointers Find the Width of the Binary Search Tree Forest trees in Data Structures Free Tree in Data Structures Frequently asked questions in Tree Data Structures Infix, Postfix and Prefix Conversion Time Complexity of Fibonacci Series What is Weighted Graph in Data Structure What is the Advantage of Linear Search?

Introduction to Huffman Coding
2023-04-05 01:16:14

Introduction to Huffman Coding

Huffman coding is a data compression technique that uses variable-length code to represent the characters in a file or data stream. The technique is named after its inventor, David A. Huffman, who published it in 1952. Huffman coding is a lossless compression technique, meaning no information is lost during the compression and decompression process. The main idea behind Huffman coding is to represent the characters that appear more frequently in the data with shorter codes while representing the characters that appear less frequently with longer codes.

Introduction to Huffman Coding

Benefits of Huffman Coding

  • One of the main benefits of Huffman coding is that it is a lossless compression technique. This means that the original data can be restored from the compressed data without any loss of information.
  • Another benefit of Huffman coding is that it is very efficient, especially for files or data streams containing many repetitive characters. The technique can also compress data in real time, making it an ideal solution for streaming video and audio.

How does Huffman Coding Work?

The basic idea behind Huffman coding is to represent the characters in a file or data stream with a variable-length code.

  • The first step in the process is to count the number of times each character appears in the data.
  • The next step is to create a binary tree where each leaf node represents a character, and the value of each node is the number of times that character appears in the data. The tree is constructed so that the character with the lowest frequency is placed at the bottom of the tree, and the characters with higher frequencies are placed higher in the tree.
  • Once the tree is constructed, assign a binary code to each character. The binary code is determined by starting at the tree's root and following the path to each character's leaf node.

The code for each character is the binary representation of the path from the root to that character's leaf node. The shorter the code for a character, the more frequently that character appears in the data.

Applications of Huffman Coding

Huffman coding is widely used in various applications, including data compression, image and video compression, audio compression, and lossless data transmission. The technique is also used in telecommunications and storing digital images and videos. Huffman coding is also used to implement certain algorithms, such as the JPEG image compression algorithm.

Advantages of Huffman Coding over Other Compression Techniques

One of the main advantages of Huffman coding over other compression techniques is its simplicity. Unlike other techniques, such as arithmetic or run-length encoding, Huffman coding can be implemented using only a few lines of code. This makes it an ideal solution for applications with limited computational resources, such as embedded systems or mobile devices.

One of the main advantages of Huffman coding over other compression techniques is its ability to provide a high compression ratio for data containing many repetitive characters. For example, text files that contain a large number of common words can be compressed to a very small size using Huffman coding.

Another advantage of Huffman coding is its ability to adapt to compressed data changes. If the frequency distribution of the characters in the data changes, the Huffman coding algorithm can easily adjust to reflect these changes without recompressing the entire data set. This makes Huffman coding an ideal solution for real-time data compression and transmission.

Efficiency and Space Complexity of Huffman Coding

Huffman coding is a very efficient compression technique.

The time complexity of the Huffman coding algorithm is O(n log n), where n is the number of characters in the data.

The space complexity of the algorithm is O(n), which requires only a moderate amount of memory to implement.

Implementation of Huffman Coding

Huffman coding can be implemented in various programming languages, including C, C++, Java, and Python. The basic steps involved in implementing Huffman coding are:

  • Count the frequency of each character in the data.
  • Create a binary tree where each leaf node represents a character, and the value of each node is the frequency of that character in the data.
  • Assign a binary code to each character based on the path from the tree's root to each character's leaf node.
  • Write the compressed data to a file or stream using the binary codes assigned to each character.

Practice Problems Based on Huffman Coding

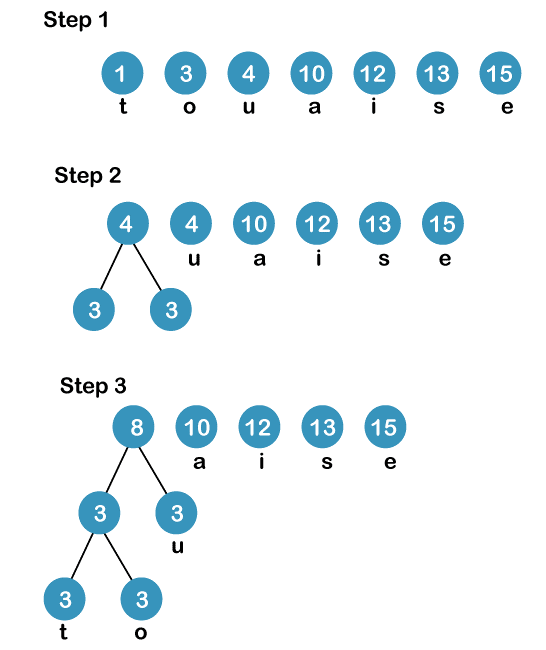
Suppose there is a file that includes different characteristics along with their corresponding frequencies. If we apply Huffman coding to compress the data in this file, what can be determined?

1.       Huffman code for each character

2.       Average code length

3.       Length of Huffman encoded message

   CHARACTERSFREQUENCIES
                E15
                I12
                03
                U4
                S13
                T                        1
A10

SOLUTION –

The process of constructing a Huffman Tree involves the following steps:-

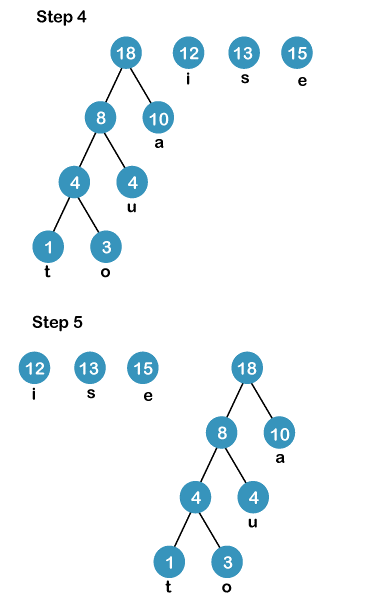
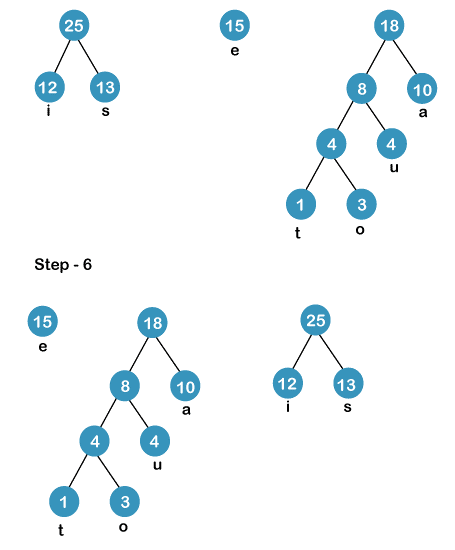
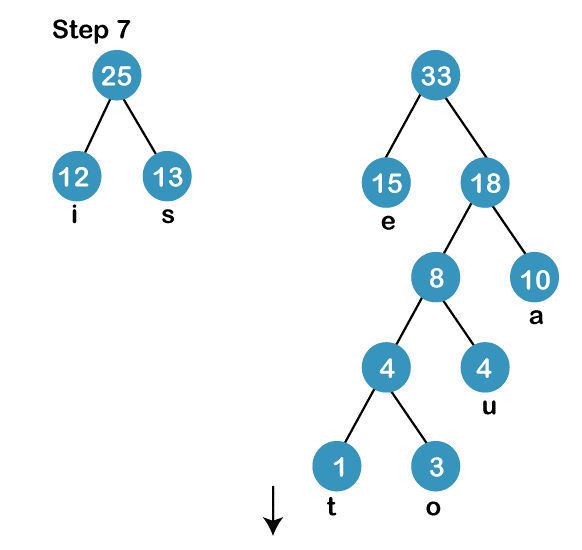
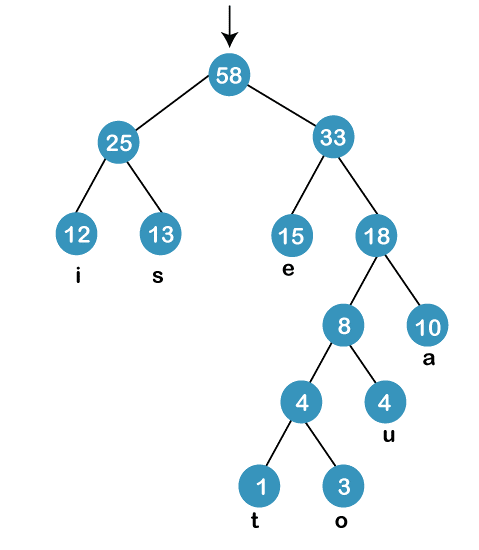
Introduction to Huffman Coding Introduction to Huffman Coding Introduction to Huffman Coding Introduction to Huffman Coding Introduction to Huffman Coding

Next,

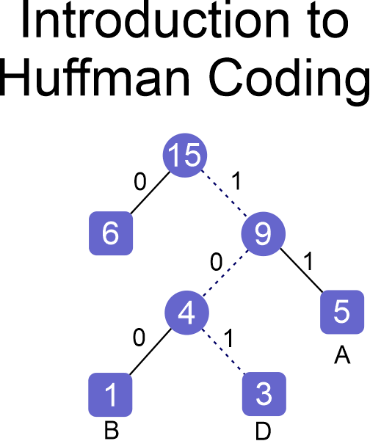
 we need to assign weights to the edges of the Huffman Tree that has been constructed. The convention is to assign the weight '0' to the edges on the left side of the tree and the weight '1' to the edges on the right side of the tree.

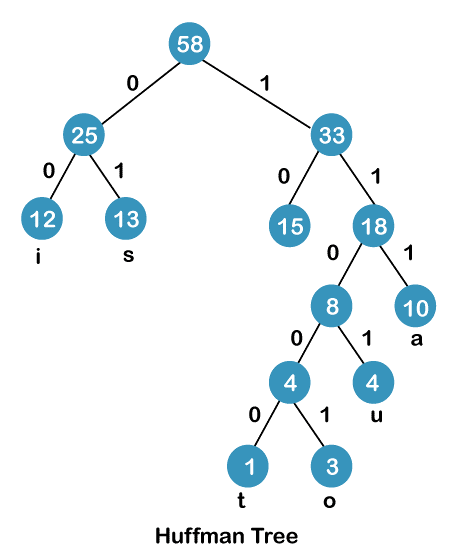
Introduction to Huffman Coding

The modified Huffman tree refers to the Huffman tree structure that has been updated with weight assignment on its edges.

Conclusion

Huffman coding is a powerful and efficient data compression technique widely used in various applications. The technique is based on representing the characters in a file or data stream with a variable-length code. The characters that appear more frequently are represented with shorter codes, and the characters that appear less frequently are represented with longer codes. Huffman coding is a lossless compression technique, meaning no information is lost during the compression and decompression process. The benefits of Huffman coding, combined with its efficiency and versatility, make it an ideal solution for a wide range of data compression and transmission applications.