Insertion Sort in Data Structures

Insertion Sort in C++

Insertion sort is a sorting algorithm that, in each iteration, installs an unsorted element in its proper position

Insertion sort operates in a similar way to how we sort cards in a card game.

We collect an unsorted card deck and we presume that the first card is already sorted that is, it is the smallest number of all. If the next card is larger than the one in hand, it goes behind; otherwise, it comes to the front. Similarly, other unordered cards are collected and Placed in the mannered way.

Insertion sort takes a similar strategy.

Algorithm

In order to sort an array of n elements in increasing order, use the following commands:

insertionSort(array)
  mark first element as sorted
  for each unsorted element X
    'extract' the element X
    for j <- lastSortedIndex down to 0
      if current element j > X
        move sorted element to the right by 1
    break loop and insert X here
end insertionSort

Insertion Sort's Operation

Consider using the array given below as an example for understanding how insertion sort works.

10

6

2

5

4

• The array's initial element is presumed to be sorted. Select the second value and place it in another key.
• Make a comparison between the first value and the key. In case the first value is bigger than key, the value is placed in front of key.

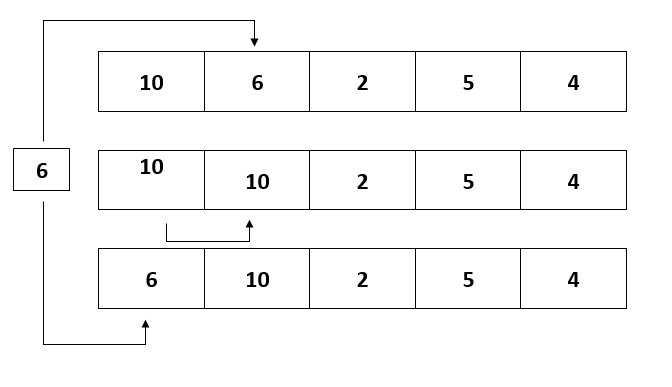
• The first two items have now been sorted.
• Now consider the third element in relation to the components on its left and place it just before the element that it is smaller than. So, placing it at the start of the array as there are no elements smaller as compared to key element.

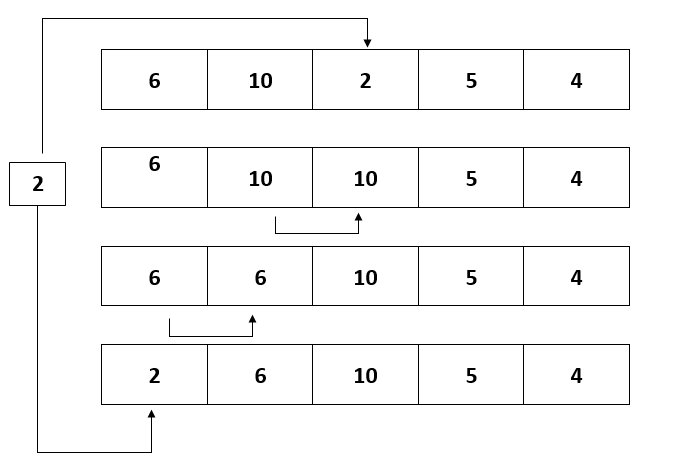
Similarly, put each unsorted element in its proper location.

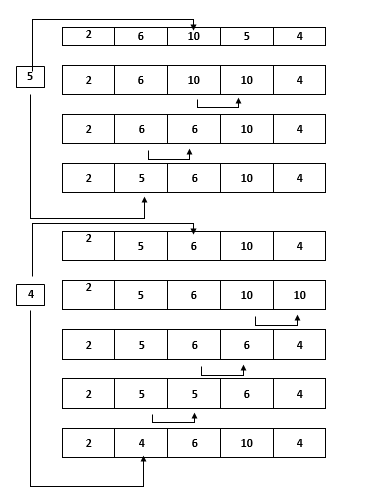
Code for Insertion Sort in c++

// Insertion sort in C++


#include <iostream>
using namespace std;


// Function for print an array
void printArray(int array[], int size) {
  for (int i = 0; i < size; i++) {
    cout << array[i] << " ";
  }
  cout << endl;
}


void insertionSort(int array[], int size) {
  for (int step = 1; step < size; step++) {
    int key = array[step];
    int j = step - 1;


    // Compare key with each element on the left of it until an element smaller than
    // it is found.
    // For descending order, change key<array[j] to key>array[j].
    while (key < array[j] && j >= 0) {
      array[j + 1] = array[j];
      --j;
    }
    array[j + 1] = key;
  }
}


// Main code
int main() {
  int data[] = {11, 9, 6, 41, 32};
  int size = sizeof(data) / sizeof(data[0]);
  insertionSort(data, size);
  cout << "Sorted array in ascending order:\n";
  printArray(data, size);
}

Output

Sorted array in ascending order:
6 9 11 32 41

Complexity for Insertion Sort

Time Complexity
Best Case	O(n)
Worst Case	O(n2)
Average	O(n2)
Space Complexity	O(1)
Stability	Yes

Complexities of Time

• Complexity in the worst-case scenario: O (n²)

Let's consider having an array that is sorted in ascending order and that is to be sorted in descending order. In this situation, worst case complexity happens.

Each and every element is to be compared to each of the other elements, resulting in a (n-1) number of comparisons for every nth element.

As a result, the total number of comparisons is equal to n*(n-1) n2.

• Complexity in the Best-Case Scenario: O (n)

When the array has already been sorted, the outer loop repeats n times, but the inner loop does not. As a result, there are only n possible comparisons. As a result, complexity follows a linear pattern.

• Case Complexity on the Average: O (n²)

When the items of an array are jumbled together, this happens (neither ascending nor descending).

Complexity of Space

Because an additional variable key is employed, the space complexity is O(1).

Applications for Insertion Sorting

The insertion sort is used in the following situations:

• When only a few elements in the array are to be sorted.
• When there are only a few components are left to sort.

What is Binary Insertion Sort, and how does it work?

In conventional insertion sort, we may employ binary search to minimize the number of comparisons. At each cycle, Binary Insertion Sort employs binary search to identify the right spot to insert the selected item. In the worst scenario, sorting in regular insertion takes O(n) (at n^th iteration). Binary search implementation, can decrease the complexity up to O(log n). Because of the multiple swapping that are necessary for each insertion, the method as a whole still has a worst-case time complexity as O(n²).