Spanning Tree
Spanning Tree: The spanning tree is a subset of the graph. It is a non-cyclic graph. If any node in the spanning tree is truncated, the entire graph fails.
There are several ways to create a spanning tree from a graph. Three types of spanning trees have been created from a graph, which has all the vertices and some edges in the graph. Ensure that no spreading trees form a circle.
Properties of the spanning tree
- The connected graph may contain more than one spanning tree.
- There is no cycle in the spanning tree.
- If any node in the spanning tree is truncated, the entire graph fails.
- If you add an edge to the spanning tree, it creates a loop or circuit.
Cost of a spanning tree
The cost of a spanning tree can be calculated by adding the weights of its vertices.
Minimum spanning tree
The minimum spanning tree is that spanning-tree, which costs the lowest.There are two types of algorithms for finding the minimum spanning tree.
- Prim's algorithm
- Kruskal's algorithm
Prim’s algorithm
Prim’s algorithm is based on the greedy algorithm. It is used to find a minimum spanning tree in the graph. This algorithm treats a single tree as a node, and adds a new node to it to create a spanning tree from the given graph.
Algorithm
Step 1. Select a starting vertex. Step 2. Repeat Steps 3 and 4 until there are fringe vertices. Step 3. Select an edge e connecting the tree vertex and fringe vertex that has minimum weight. Step 4. Add the selected edge and the vertex to the minimum spanning tree T. Step 5. Exit.
Example of prim’s algorithm
Construct the MST for the given graph in the following figure using Prime's algorithm.
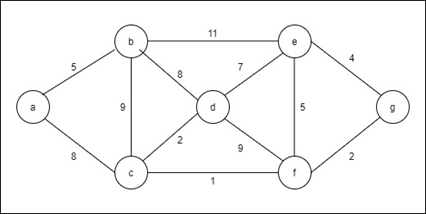
Step 1: Choose a vertex S = {a} V/S = {b, c, d, e, f, g}
Step 2: Choose the shortest edge from this vertex, and add it. S = {a} V/S = {b, c, d, e, f, g} Lowest edge = {ab}
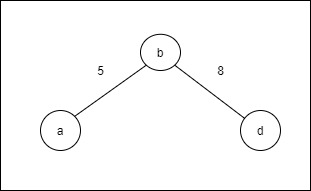
Step 3: Choose the shortest edge from the b vertex and add it. S = {a, b} V/S = {c, d, e, f, g} Lowest edge = {bd}
Step 4: Choose the shortest edge from the d vertex and add it. S = {a, b, d} V/S = {c, e, f, g} Lowest edge = {dc}
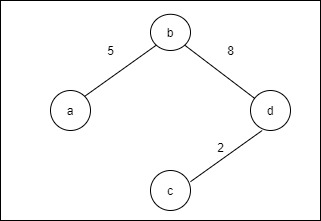
Step 5: Choose the shortest edge from the c vertex and add it. S = {a, b, d, c} V/S = {e, f, g} Lowest edge = {cf}
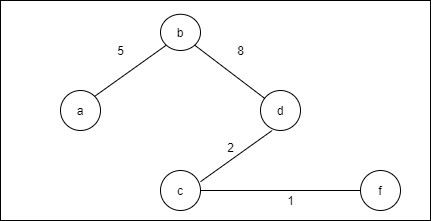
Step 6: Choose the shortest edge from the f vertex and add it. S = {a, b, d, c, f} V/S = {e, g} Lowest edge = {fg}
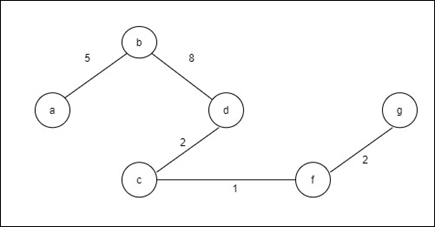
Step 7: Choose the shortest edge from the g vertex and add it. S = {a, b, d, c, f, g} V/S = {e} Lowest edge = {ge}
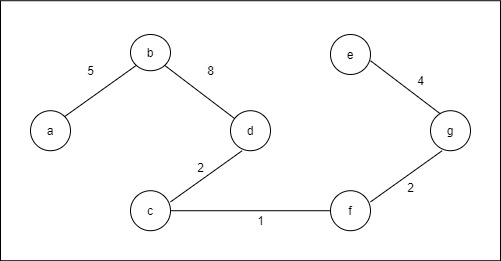
MST is complete MST cost = 5 + 8 + 2 + 1 + 2 + 4 = 22
Prim’s algorithm program in C language
#include <stdio.h>
#include <conio.h>
#include <limits.h>
#define vertices 5
int minimum_key(int k[], int mst[])
{
int minimum = INT_MAX, min,i;
for (i = 0; i < vertices; i++)
if (mst[i] == 0 && k[i] < minimum )
minimum = k[i], min = i; return min;
}
void prim(int g[vertices][vertices])
{
int parent[vertices];
int k[vertices];
int mst[vertices];
int i, count,u,v;
for (i = 0; i < vertices; i++)
k[i] = INT_MAX, mst[i] = 0;
k[0] = 0;
parent[0] = -1;
for (count = 0; count < vertices-1; count++)
{
u = minimum_key(k, mst);
mst[u] = 1;
for (v = 0; v < vertices; v++)
if (g[u][v] && mst[v] == 0 && g[u][v] < k[v])
parent[v] = u, k[v] = g[u][v];
}
for (i = 1; i < vertices; i++)
printf("%d %d %d \n", parent[i], i, g[i][parent[i]]);
}
void main()
{
int g[vertices][vertices] = { {3, 2, 1, 9, 0}, {5, 1, 2, 10, 4}, {0, 4, 1, 0, 9}, {8, 10, 0, 2, 10}, {1, 6, 8, 11, 0} };
prim(g); }
Output:
0 1 5 0 2 0 0 3 8 1 4 6
Kruskal’s algorithm
Kruskal’s algorithm is also based on the greedy algorithm. Kruskal’s algorithm is used to find a minimum spanning tree in a graph. It follows all properties of the minimum spanning tree. In this algorithm, a graph is treated as a forest and all nodes are treated as an individual tree.
To find the minimum spanning tree with the help of Kruskal algorithm, firstly we choose a lowest cost edge in the graph. After that, again, we choose the second lowest cost edge, and the process continues until all the vertices have been added.
Algorithm
MST_Kruskal’s(G, v) Step 1: for each vartex V in graph G do Step 2: create a set (actually tree) with element v Step 3: Initialize a pririty queue ‘Q’ containing all edges in descending order of their weight Step 4: Forest ? A //contain all edges of the MST Step 5: while Tree (T) has edges <= N-1 do // N is no of vertices Step 6: Select edge with minimum weight Step 7: if T(v) ? T(u) then add (u, v) to forest union T(v) and T(u) Step 8: return
Example of Kruskal’s algorithm
Construct the MST for the given graph in the following figure using Kruskal’s algorithm.
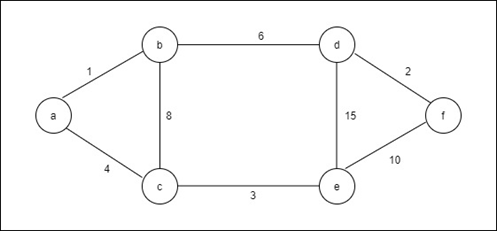
Solution:
| Edge | ab | df | ce | ac | bd | bc | ef | de |
| Weight | 1 | 2 | 3 | 4 | 6 | 8 | 10 | 15 |
Step 1:
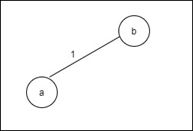
Step 2:
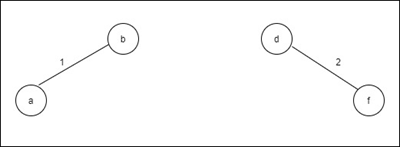
Step 3:
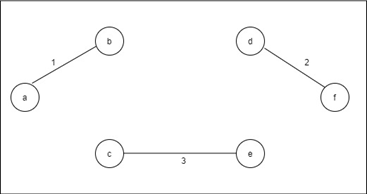
Step 4:
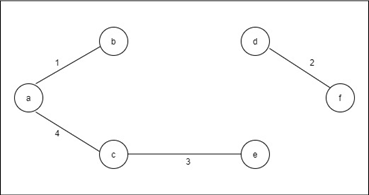
Step 5:
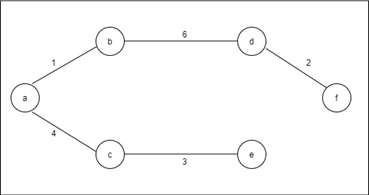
MST is complete
Kruskal’s algorithm program in C language
#include <iostream>
#include <vector>
#include <utility>
#include <algorithm>
using namespace std;
const int MAX = 1e4 + 5;
int id[MAX], nodes, edges;
pair <long long, pair<int, int> > p[MAX];
void init()
{
for(int i = 0;i < MAX;++i)
id[i] = i;
}
int root(int x)
{
while(id[x] != x)
{
id[x] = id[id[x]];
x = id[x];
}
return x;
}
void union1(int x, int y)
{
int p = root(x);
int q = root(y); id[p] = id[q];
} long long kruskal(pair<long long, pair<int, int> > p[])
{
int x, y;
long long cost, minimumCost = 0; for(int i = 0;i < edges;++i)
{
x = p[i].second.first;
y = p[i].second.second;
cost = p[i].first;
if(root(x) != root(y))
{
minimumCost += cost;
union1(x, y);
}
}
return minimumCost;
}
int main()
{
int x, y;
long long weight, cost, minimumCost;
init(); cout <<"Enter Nodes and edges";
cin >> nodes >> edges;
for(int i = 0;i < edges;++i)
{
cout<<"Enter the value of X, Y and edges";
cin >> x >> y >> weight;
p[i] = make_pair(weight, make_pair(x, y));
}
sort(p, p + edges);
minimumCost = kruskal(p);
cout <<"Minimum cost is "<< minimumCost << endl; return 0; }