Operations on 2D-Arrays
Two Dimensional Array Operations
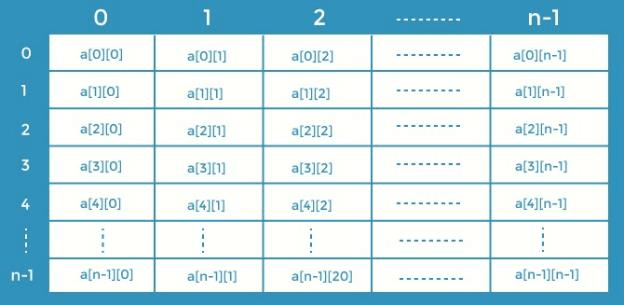
Adding Elements to Two-D Arrays
We must put data in both rows and columns when inserting items in 2-D Arrays. As a result, we employ the idea of loops. We had present the values in the above method for initialising the data in an array.
The user can dynamically put things here according to their needs. An example of code for adding the items is shown below.
#include <stdio.h>int main(){ int arr[2][3]; int i,j,num; printf("Enter elements into 2-D array: "); for(i=0;i<2;i++) { for(j=0;j<3;j++) { scanf("%d" , &arr[i][j]); } } printf("Entered values into 2-D array: "); for(i=0;i<2;i++) { for(j=0;j<3;j++) { printf("%d" , arr[i][j]); } printf("\n"); }} |
The following output should be generated by this programme:
As may be seen in the code:
- First, we declare the array variable, as well as the array's dimensions, which include the number of rows and columns.
- Then we declare two variables for iterating through the array's elements.
- The loops are then utilised. The outside for loop iterates the rows, while the inside loop iterates the columns.
- The scanf function is used to read the data as it is entered and then inserts the value at the I and j places.
In the preceding example, the data was entered into a matrix with two rows and three columns. The following can be obtained as a result of the following:
Output
Enter elements into 2-D array:
1
2
3
4
5
6
Entered values into 2-D array
123
456
Converting a 2D array to a 1D array
2D arrays are mostly used to construct a data structure that resembles a database table. The storing strategy for 2D arrays in computer memory is identical to that of a one-dimensional array.
The product of the number of rows and the number of columns in a 2D array is always equal to the array's size. As a result, in order to store two-dimensional arrays in memory, we must map them to one-dimensional arrays.
The graphic below depicts a 3 X 3 2D array.
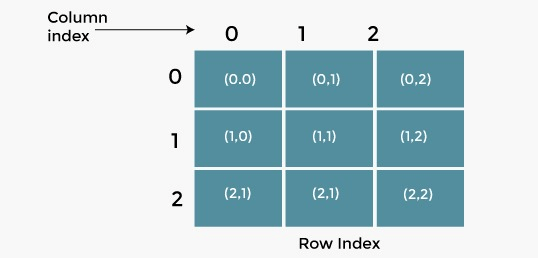
To convert a two-dimensional array to a one-dimensional array, there are two methods.
Row Major Ordering –
All the rows of the two-dimensional array are stored in a continuous way in memory when row major ordering is used. The memory allocation for the array displayed in the above image using the row major order approach is illustrated below.

The items of the first row of the 2D array are first inserted into memory, followed by the elements of the second row, and so on.
C code implementation
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
int main()
{
int array2D[10][10], * arr1D;
int n, m, i, j;
// Enter Matrix A
printf("Enter Number of Rows: ");
scanf("%d", &n);
printf("Enter Number of columns: ");
scanf("%d", &m);
printf("Enter 2D Array: \n");
for (i = 0; i < n; ++i) {
for (j = 0; j < m; ++j) {
scanf("%d", &array2D[i][j]);
}
}
// allocating memeory to 1D dynamically
// size of 1D array will be n*m
arr1D = (int*)malloc(n * m * sizeof(int));
for (i = 0; i < n; ++i) {
for (j = 0; j < m; ++j) {
// mapping 1D array to 2D array
array1D[i * m + j] = array2D[i][j];
}
}
printf("1D Array: ");
for (i = 0; i < n * m; ++i) {
printf("%d ", array1D[i]);
}
}
The following output should be generated by this programme:
Output
Enter Number of Rows: 3
Enter Number of columns: 3
Enter 2D Array:
10 10 10
20 20 20
30 30 30
1D Array: 10 10 10 20 20 20 30 30 30
Column Major Ordering –
All of the columns of the two-dimensional array are stored in the memory in a continuous manner in column major ordering. The memory allocation for the array displayed in the above image using the column major order approach is illustrated below.

The items of the first column of the 2D array are first inserted into memory, followed by the elements of the second column, and so on.
C code implementation
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
int main()
{
int array2D[10][10], * arr1D;
int n, m, i, j;
// Enter Matrix A
printf("Enter Number of Rows: ");
scanf("%d", &n);
printf("Enter Number of columns: ");
scanf("%d", &m);
printf("Enter 2D Array: \n");
for (i = 0; i < n; ++i) {
for (j = 0; j < m; ++j) {
scanf("%d", &array2D[i][j]);
}
}
// allocating memeory to 1D dynamically
// size of 1D array will be n*m
arr1D = (int*)malloc(n * m * sizeof(int));
for (j = 0; j < m; ++j) {
for (i = 0; i < n; ++i) {
// mapping 1D array to 2D array
array1D[j * n + i] = array2D[i][j];
}
}
printf("1D Array: ");
for (i = 0; i < n * m; ++i) {
printf("%d ", array1D[i]);
}
}
The following output should be generated by this programme:
Output
Enter Number of Rows: 3
Enter Number of columns: 3
Enter 2D Array:
10 10 10
20 20 20
30 30 30
1D Array: 10 20 30 10 20 30 10 20 30
Using Multi-dimensional Arrays, a C programme to add two matrices
C code implementation
#include <stdio.h>
int main() {
int row, column, array1[100][100], array2[100][100], S[100][100], i, j;
printf("Enter the number of rows (between 1 and 100): ");
scanf("%d", &row);
printf("Enter the number of columns (between 1 and 100): ");
scanf("%d", &column);
printf("\nEnter elements of 1st matrix:\n");
for (i = 0; i < row; ++i)
for (j = 0; j < column; ++j) {
printf("Enter element a%d%d: ", i + 1, j + 1);
scanf("%d", &array1[i][j]);
}
printf("Enter elements of 2nd matrix:\n");
for (i = 0; i < row; ++i)
for (j = 0; j < column; ++j) {
printf("Enter element b%d%d: ", i + 1, j + 1);
scanf("%d", &array2[i][j]);
}
// adding two matrices
for (i = 0; i < row; ++i)
for (j = 0; j < column; ++j) {
S[i][j] = array1[i][j] + array2[i][j];
}
// printing the result
printf("\nSum of two matrices: \n");
for (i = 0; i < row; ++i)
for (j = 0; j < column; ++j) {
printf("%d ", S[i][j]);
if (j == column - 1) {
printf("\n\n");
}
}
return 0;
}
The following output should be generated by this programme:
Output
Enter the number of rows (between 1 and 100): 3
Enter the number of columns (between 1 and 100): 2
Enter elements of 1st matrix:
Enter element a11: 5
Enter element a12: 2
Enter element a21: 4
Enter element a22: 9
Enter element a31: -6
Enter element a32: 1
Enter elements of 2nd matrix:
Enter element b11: 4
Enter element b12: -5
Enter element b21: 13
Enter element b22: 7
Enter element b31: 2
Enter element b32: 1
Sum of two matrices:
9 -3
17 16
-4 2
The user is prompted to input the number of rows r and columns c in this software. The user is next prompted to input the elements of the two matrices (of order rxc).
We then combined the elements of two matrices and stored the result in a new matrix (two-dimensional array). Finally, the outcome is shown on the computer screen.
Multiplying Two Matrices in C Using Multi-dimensional Arrays
This application requires the user to specify the dimensions of two matrices (rows and columns).
To multiply two matrices, the first matrix's number of columns must equal the second matrix's number of rows.
Until the aforesaid condition is met, the programme below requests the number of rows and columns of two matrices.
After that, two matrices are multiplied, and the result is presented on the screen.
We've written three functions to help us with this:
- getElementsofMatrix() takes user-supplied matrix elements.
- martrixMultiplication() is a function that allows you to multiply two matrices.
- print() is used to show the resulting matrix after it has been multiplied.
C code implementation
#include <stdio.h>
// function to get matrix elements entered by the user
void getElementsofMatrix(int matrix[][10], int row, int column) {
printf("\nEnter elements: \n");
for (int i = 0; i < row; ++i) {
for (int j = 0; j < column; ++j) {
printf("Enter a%d%d: ", i + 1, j + 1);
scanf("%d", &matrix[i][j]);
}
}
}
// function to multiply two matrices
void matrixMultiplication(int first[][10],
int second[][10],
int result[][10],
int row1, int column1, int row2, int column2) {
// Initializing elements of matrix mult to 0.
for (int i = 0; i < row1; ++i) {
for (int j = 0; j < column2; ++j) {
result[i][j] = 0;
}
}
// Multiplying first and second matrices and storing it in result
for (int i = 0; i < row1; ++i) {
for (int j = 0; j < column2; ++j) {
for (int k = 0; k < column1; ++k) {
result[i][j] += first[i][k] * second[k][j];
}
}
}
}
// function to print the matrix
void print(int result[][10], int row, int column) {
printf("\nOutput Matrix:\n");
for (int i = 0; i < row; ++i) {
for (int j = 0; j < column; ++j) {
printf("%d ", result[i][j]);
if (j == column - 1)
printf("\n");
}
}
}
int main() {
int first[10][10], second[10][10], result[10][10], row1, column1, row2, column2;
printf("Enter rows and column for the first matrix: ");
scanf("%d %d", &row1, &column1);
printf("Enter rows and column for the second matrix: ");
scanf("%d %d", &row2, &column2);
// Taking input until
// 1st matrix columns is not equal to 2nd matrix row
while (column1 != row2) {
printf("Error! Enter rows and columns again.\n");
printf("Enter rows and columns for the first matrix: ");
scanf("%d%d", &row1, &column1);
printf("Enter rows and columns for the second matrix: ");
scanf("%d%d", &row2, &column2);
}
// get elements of the first matrix
getElementsofMatrix(first, row1, column1);
// get elements of the second matrix
getElementsofMatrix(second, row2, column2);
// multiply two matrices.
matrixMultiplication(first, second, result, row1, column1, row2, column2);
// print the result
print(result, row1, column2);
return 0;
}
The following output should be generated by this programme:
Output
Enter rows and column for the first matrix: 2
3
Enter rows and column for the second matrix: 3
4
Enter elements:
Enter a11: 2
Enter a12: 1
Enter a13: 4
Enter a21: 0
Enter a22: 1
Enter a23: 1
Enter elements:
Enter a11: 6
Enter a12: 3
Enter a13: -1
Enter a14: 0
Enter a21: 1
Enter a22: 1
Enter a23: 0
Enter a24: 4
Enter a31: -2
Enter a32: 5
Enter a33: 0
Enter a34: 2
Output Matrix:
5 27 -2 12
-1 6 0 6
Finding the Transpose of a Matrix in C.
The transpose of a matrix is the creation of a new matrix by swapping the rows and columns.
The user is prompted to input the number of rows r and columns c in this software. In this software, their values should be fewer than ten.
The user is then requested to enter the matrix's elements (of order r*c).
The software below then computes the matrix's transpose and displays it on the screen.
Hence, Matrix B is said to be the transpose of Matrix A if its rows are the columns of the original matrix. For example, if A and B are two matrices and Matrix B's rows are the columns of Matrix A, Matrix B is said to be the transpose of Matrix A.
The following reasoning was used to convert the m(i,j) matrix to m(j,i):
Algorithm
#include <stdio.h>
int main() {
int a[10][10], trans[10][10], row, column;
printf("Enter rows and columns: ");
scanf("%d %d", &row, &column);
// asssigning elements to the matrix
printf("\nEnter matrix elements:\n");
for (int i = 0; i < row; ++i)
for (int j = 0; j < column; ++j) {
printf("Enter element a%d%d: ", i + 1, j + 1);
scanf("%d", &a[i][j]);
}
// printing the matrix a[][]
printf("\nEntered matrix: \n");
for (int i = 0; i < row; ++i)
for (int j = 0; j < column; ++j) {
printf("%d ", a[i][j]);
if (j == column - 1)
printf("\n");
}
// computing the transpose
for (int i = 0; i < row; ++i)
for (int j = 0; j < column; ++j) {
trans[j][i] = a[i][j];
}
// printing the transpose
printf("\nTranspose of the matrix:\n");
for (int i = 0; i < column; ++i)
for (int j = 0; j < row; ++j) {
printf("%d ", trans[i][j]);
if (j == row - 1)
printf("\n");
}
return 0;
}
C code implementation
#include <stdio.h>
int main() {
int a[10][10], trans[10][10], row, column;
printf("Enter rows and columns: ");
scanf("%d %d", &row, &column);
// asssigning elements to the matrix
printf("\nEnter matrix elements:\n");
for (int i = 0; i < row; ++i)
for (int j = 0; j < column; ++j) {
printf("Enter element a%d%d: ", i + 1, j + 1);
scanf("%d", &a[i][j]);
}
// printing the matrix a[][]
printf("\nEntered matrix: \n");
for (int i = 0; i < row; ++i)
for (int j = 0; j < column; ++j) {
printf("%d ", a[i][j]);
if (j == column - 1)
printf("\n");
}
// computing the transpose
for (int i = 0; i < row; ++i)
for (int j = 0; j < column; ++j) {
trans[j][i] = a[i][j];
}
// printing the transpose
printf("\nTranspose of the matrix:\n");
for (int i = 0; i < column; ++i)
for (int j = 0; j < row; ++j) {
printf("%d ", trans[i][j]);
if (j == row - 1)
printf("\n");
}
return 0;
}
The following output should be generated by this programme:
Output
Enter rows and columns: 2
3
Enter matrix elements:
Enter element a11: 10
Enter element a12: 20
Enter element a13: 30
Enter element a21: 40
Enter element a22: 50
Enter element a23: 60
Entered matrix:
10 20 30
40 50 60
Transpose of the matrix:
10 40
20 50
30 60