What is a Threaded Binary Tree?

When we consider those binary trees that are interlinked with each other, we do come across the fact that the fields present in there do consist of NULL values that ultimately lead to the damage and wastage of the storage space that we use for the tree. If we have a binary tree that comprises n number of nodes, then the n+1 link fields would definitely have the NULL values.

In order to save and manage the wastage of this storage space, a new convention was introduced by two people named Perlis and Thornton. In this particular method, the links which were previously filled with NULL are significantly replaced by threads. So, the binary trees that contains threads as a replacement, those binary trees are termed threaded binary trees. Each and every node in a threaded binary tree either contain a link to their child node or thread to various other nodes present in the tree.

Types of threaded binary tree

There are majorly two types of the threaded binary trees. They are given below: -

• One-way threaded binary tree
• Two-way threaded binary tree

Now, we will explain each of these trees one by one in the given section.

One-way threaded binary tree

In this type of threaded binary tree, the thread usually occurs either at the left or right link of the field of a given node. If, for example, say the link pops up at the right link of the field, then it will ultimately lead and point to the next adjacent node that will appear and perform the inorder traversal operation on the tree.

Such types of trees are vividly known as the Right threaded binary trees. Whereas on the other hand, if suppose the link pops out at the left link of a given node, then it will ultimately lead and point to the next adjacent node that will appear and perform the inorder predecessor operation on the tree. Such types of trees are known as the left threaded binary trees. In such kind of threaded binary trees, the right link of the last node and the left link of the first node generally occupies a NULL value.

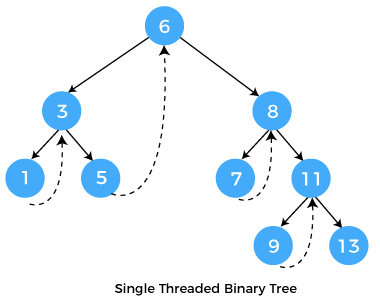
A question arises here how do we distinguish links from threads so the answer to the same question is that threads are generally denoted by dotted lines and are pretty visible to human eyes as well.

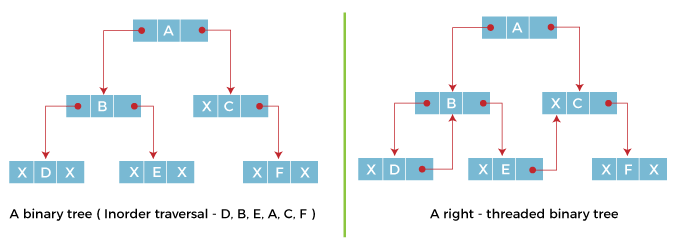
The above picture depicts that the inorder traversal and exploration of the threaded binary tree turns out to be vivid with the nodes D, B, E, A, C, and F. When this given tree is represented as the right threaded binary tree, the right link present on the tree placed on the leaf node D that also contains NULL value is generally exchanged with a thread which is represented by a dotted line. This node directly heads out and points to node B, which is the successor of node D. Likewise, in the same way, all the other trees are allotted threads.

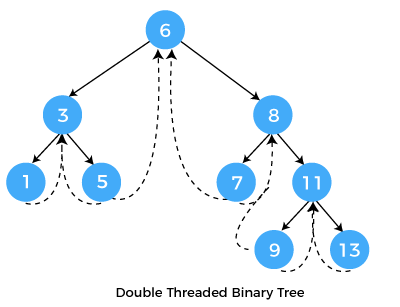
Two-way threaded binary tree

In this type of threaded binary tree, the right link of the node which contains the NULL value is generally changed by the thread that usually enacts and points out to the nodes that are inorder successor and the left link of the node which also contains the NULL value is generally replaced by the thread. It points out the nodes that are present in the inorder predecessor.

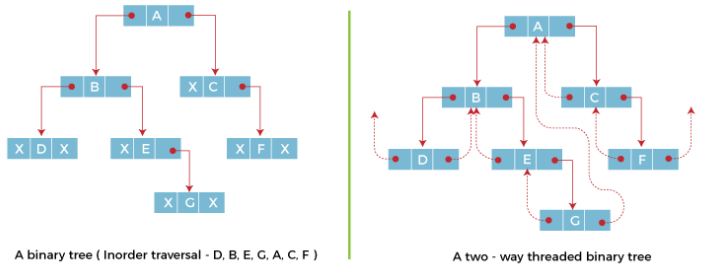
Take a look at the above picture that shows us the inorder traversal of the threaded binary tree having the vertices D, B, E, G, A, C, and F. If we look at this threaded binary tree, the node that is named E that contains the value NULL is generally interchanged by a simple thread which is a dotted line to its inorder former which node B.

Likewise, the node G that we see in the above picture contains left and right field links that already contain NULL values that are also exchanged by threads which are represented by dotted lines. This is done in such a way that the right link field generally points inorder successor, and in the same manner the left link heads out to the inorder predecessor. In the same manner, all the nodes that are present in the field are allotted threads.