Bubble Sort vs Heap Sort

In this article, we are going to compare the two most common sorting techniques, Bubble Sort and Heap sort. Before discussing their differences, let us first discuss the idea of sorting a list of elements using these sorting algorithms.

How does bubble-sort sort a list of elements?

Bubble Sort –The bubble sort uses the ‘Subtract and Conquer’ technique to sort elements. In which it continuously compares all the elements and places all the elements in their right order. It is called bubble sort because it only compares two adjacent elements referred to as the bubble at any instant.

On each iteration, the largest of two adjacent elements gets placed at the right of the smallest one, and after completion of the loop, the largest element gets placed at the end of the unsorted part of the array.

The pseudo-code of the bubble-sort function:

1. Bubble Sort (A, N)
2.	For I = 1 to N - 1
3.		For J = 0 to N - I – 1
4.			If A[J] > A[J + 1]
5.				Swap (A[j], A[j + 1])
// Where N is the size of the array A

The above pseudo code consists of nested for-loops, the internal for-loop from 0 and ends at N – I – 1, and the external for loop begins from 0 and ends at N – 2. In the if-condition, it checks the order of two adjacent elements present at index J and J + 1 and swaps them if the smaller element is on the right side of the larger one.

Now, we let us see the stages of the array after each completion of the internal for-loop through an example.

Q. Consider an array A[] = {12, 25, 15, 22, 17, 8, 19} with seven element. Show the steps involved in sorting the given array using bubble sort.

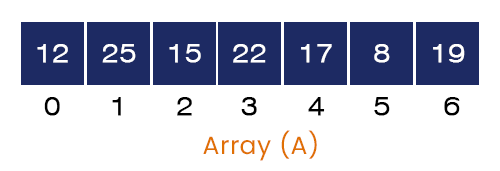
• In the first iteration the value of I = 1 and J = 0 to 7 – 1 – 1 = 5
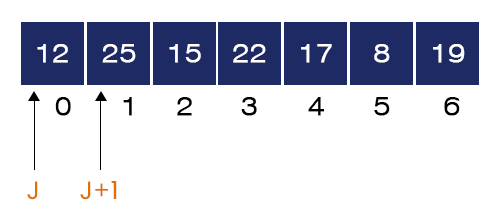
  • The value of J = 0: we have A[0] = 12 and A[1] = 25. Now, we check the if-condition here. It fails as A[1] > A[0].

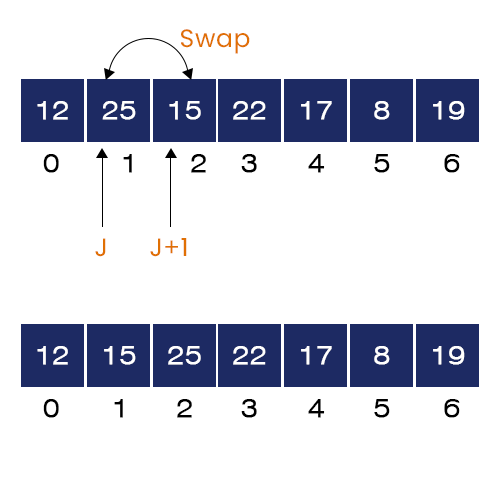
• The value of J = 1. We have A[1] = 25 and A[2] = 15. Now, we check the if-condition. Here, it is satisfied because A[2] > A[1]. Hence, we swap these two values. Now, the array will look like as shown in the figure.

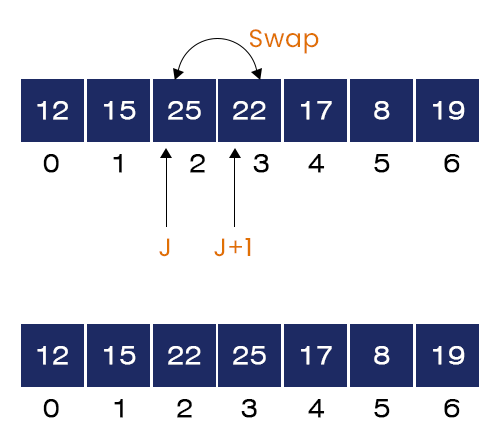
• The value of J = 2. We have A[2] = 25 and A[3] = 22. Now, we check the if-condition. Here it is satisfied because A[2] > A[1]. Hence, we swap these two values. Now, the array will look like as shown in the figure.

• The value of J = 3. We have A[3] = 25 and A[4] = 17. If-condition, is satisfied because A[2] > A[1]. Hence, we swap these two values.

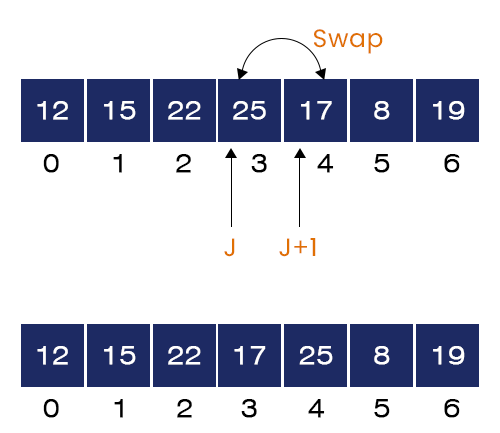
• The value of J = 4. We have A[4] = 25 and A[5] = 8. If-condition is satisfied because A[2] > A[1]. Hence, we swap these two values.

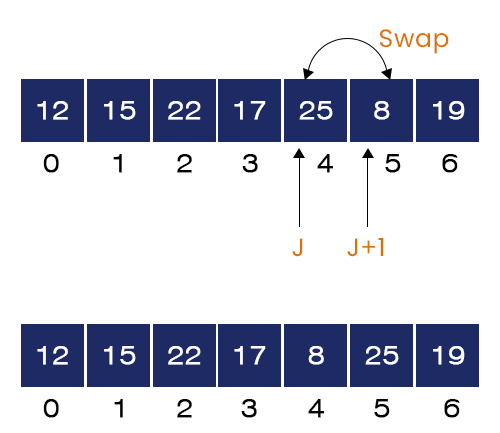
• The value of J = 5. We have A[5] = 25 and A[6] = 19. If-condition is satisfied because A[2] > A[1]. Hence, we swap these two values:

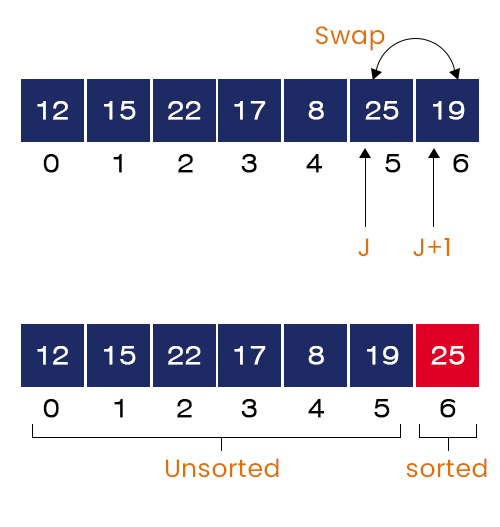
After the first iteration of the external for-loop is completed, the largest value = 25 is placed at its correct position in the array.

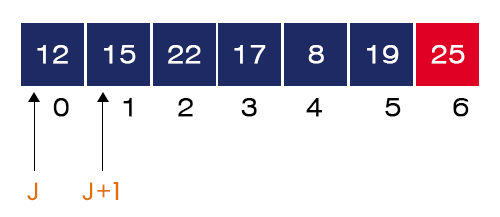
• Second Iteration – I = 2, J = 0 to 7 – 2 – 1 = 4
  • The value of J = 0. We have A[0] = 12 and A[1] = 15 and 15 > 12. Here, the if-condition is not satisfied.

• The value of J = 1. We have A[1] = 15 and A[2] = 22 and 22 > 15. Here again, the if-condition is not satisfied.

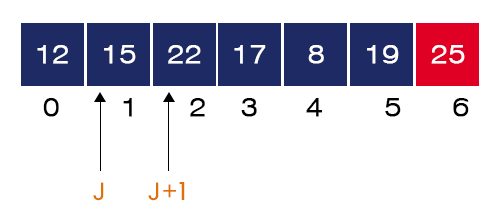
• The value of J = 2. We have A[2] = 22 and A[3] = 17 and 22 > 17. Here, the if-condition is satisfied. We swap these two elements.

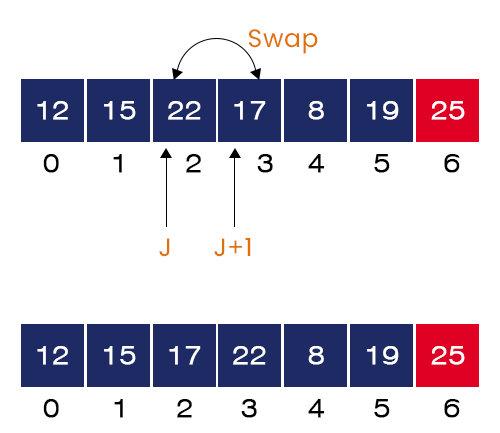
• The value of J = 3. We have A[3] = 22 and A[4] = 8 and 22 > 8. Here, the if-condition is satisfied. We swap these two elements.

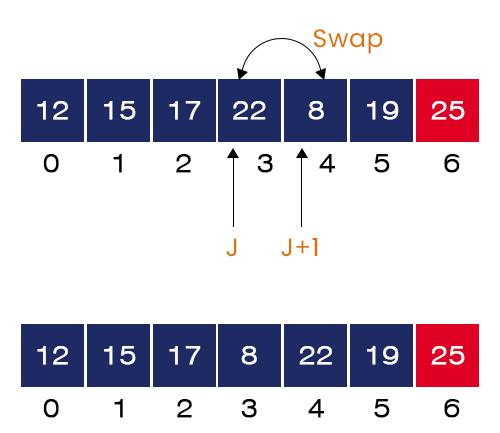
• The value of J = 4. We have A[4] = 22 and A[5] = 19 and 22 > 19. Here, the if-condition is satisfied. We swap these two values and move to the next iteration

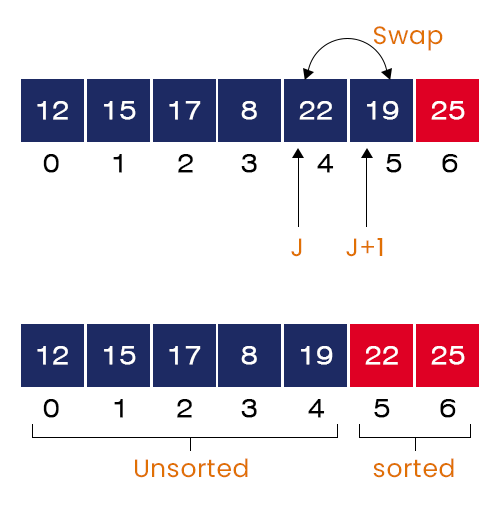
After the second iteration of the external for-loop is completed, the second largest value = 22 is placed at its correct position in the array.

• Third Iteration – I = 3, J = 0 to 3
  • We repeat the same steps as above, and at the end of the third iteration, the third largest element = 19 gets placed at its correct position in the array.

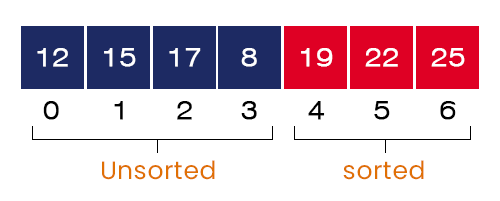
• Fourth Iteration – I = 4, J = 0 to 2
  • Similarly, after completion of the fourth iteration, the fourth largest value = 17 takes its correct position in the array.

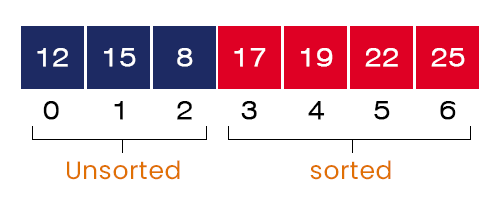
• Fifth Iteration – I = 5, J = 0 to 1
  • After completion of the fifth iteration, the fifth largest value = 15 gets placed at its correct position in the array.

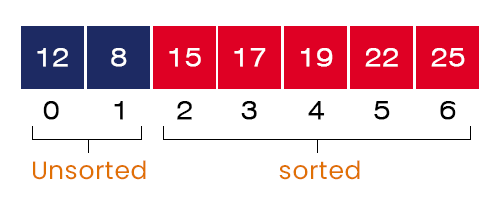
• Sixth Iteration – I = 6, J = 0 to 0
  • After completing the sixth iteration, the sixth largest value = 12 gets placed at its correct position, and the smallest element = 8 takes its correct position in the array itself.

After complete execution of the external for loop, we get the sorted array as the program’s output:

How does heap-sort sort a list of elements?

Heap – In the data structure, A heap is categorised into Min-heap and Max-heap. For all the nodes in a heap, if the parent node is smaller than its children, it is called a min-heap, and if the parent node is greater than its children, it is called a max-heap.

Heap Sort – The heap sort is based on the ‘divide and conquer’ sorting technique which uses the idea of a heap. It converts the given array into a heap first. After that, it selects the root places it at its correct position in the array and recursively repeats the same process for the remaining elements until the array gets sorted.

The heap sort algorithm consists of three main blocks/functions, Build max heap, Max heapify, and Heap Sort functions.

The pseudo-code of the heap-sort function is given below:

1. Heap Sort (A, N)
2.	Heap size = n;
3.	Build max heap (A, Heap size);
4.	For I = N - 1 down to 2
5.		Swap (A[1] and A[I]);
6.		Heap size = Heap size – 1;
7.		Build max heap (A, Heap size);

The pseudo-code of the Build max heap function:

1. Build max heap (A, Heap size)
2.	For I = Heap size / 2 down to 1
3.		Max heapify (A, I);

The pseudo-code of the Max Heapify function:

1. Max heapify (A, I)
2.	L = Left (I) // L points to the Left child of I
3.	R = Right (I) // R points to the Right child of I
4.	Largest = I


5.	If (L <= Heap Size(A) and A[L] > A[Largest])
6.		Largest = L


7.	If (R <= Heap Size(A) and A[R] > A[Largest]
8.		Largest = R


9.	If (Largest != I)
10.		Swap (A[Largest] and A[I])
11.		Max heapify (A, Largest)

The above three function blocks involved in the heap sort function are recursively called. The heap sort function calls the Build Max heap function, and the Build Max heap function calls the Max Heapify function. The build max heap function converts the given array into a Max heap, and the Max heapify function places all the elements at their correct position in a max heap.

Let us now understand the steps involved in sorting an array using heap sort through an example:

Consider an array A[] = {15, 30, 17, 22, 25, 19} with six elements in its. The steps involved in sorting the given array using the heap sort are listed below:

Step 1 – When we call the heap sort function Heap Sort (A, 6), it instantly calls the build max heap function with the same parameters Build Max Heap (A, 6), and the build max heap converts the array into a max heap. The resultant max heap is shown in the figure below:

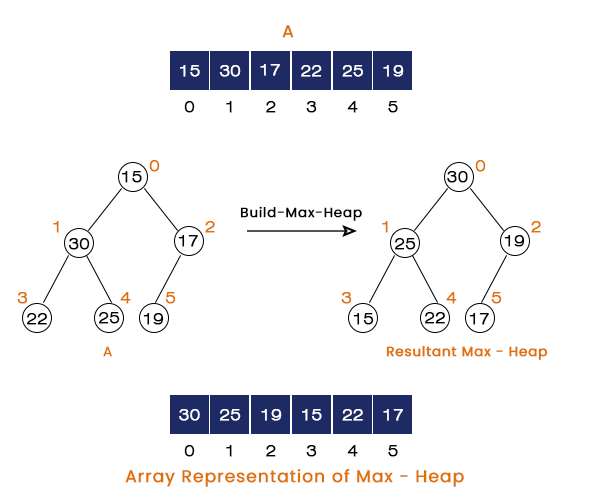
Step 2 - We first swap the element present at index zero = 30 with the element present at last index = 17. As we can see, the largest element gets placed at its right position in the array. Now, the build max heap function calls the Max heapify at the index 0 to place 17 at its correct position in a max heap.

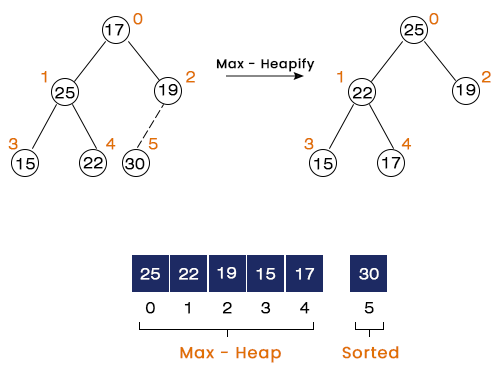
Step 3 – Here, we swap 25 with 17. After that, we call the max heapify to convert it into a max heap. The same is shown in the figure below:

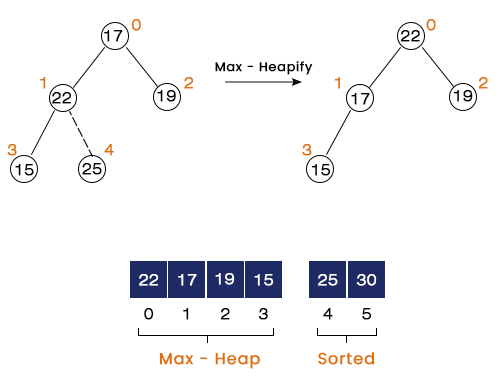
Step 4 – Here, we swap 22 with 15 and call the max heapify at index = 0 to convert the remaining part of the array into a max heap. The same is shown in the figure below:

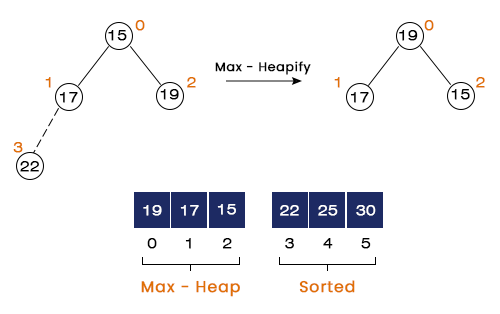
Step 5 – Here, we swap 19 with 15 and call the max heapify function at index = 0.

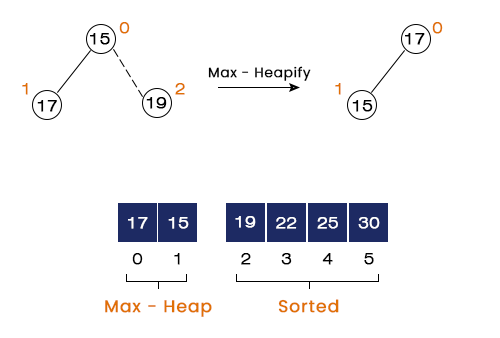
Step 6 – here, we swap 17 with 15 and call the max heapify function at index = 0, but it will make no change as only one element remains in the heap.

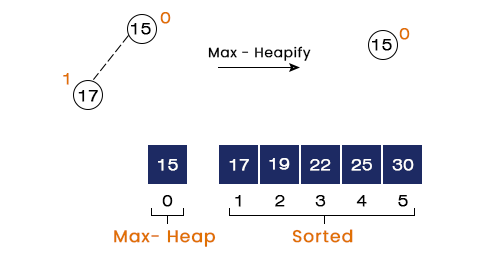
Now, the program terminates here, and we get a sorted array A as the program’s output.

Now, Let us discuss the differences between Bubble Sort and Heap Sort. The main differences between these two-sorting techniques are listed below in the table:

	Bubble Sort	Heap Sort
Definition	The bubble sort repeatedly compares the adjacent elements and swaps them if they are not in the correct order.	The heap sort uses the idea of heap data structure to sort an array by converting them into a heap and placing the root element at its correct position. It repeats the same process for the remaining part.
Approach	It is based on the subtract and conquer method.	It acts like the divide and conquer technique and achieves the time complexity of nlogn.
Time complexities	Best Case – T(n) = O(n), Average and Worst Cases – T(n) = O(n^2).	The best, average, and worst cases time complexities are O(nlogn).
Best Case Difference	When we pass a sorted array to the bubble sort, its time complexity becomes equal to O(n). This is because of its flag version, where it predetermines whether the array is sorted or not in the first run and terminates itself.	When we pass a sorted array to the heap sort, it does not change its nature and continuously repeats all the processes.
Recurrence relation	The recurrence relation of the bubble sort is T(n) = T(n-1) + n.	The recurrence relation of the heap sort is T(n) = T(n-1) + log2(n).
Stability	Yes, the order of similar elements does not change.	No, the order of similar elements may vary.
Complexity	It is less complex than the heap sort.	It is more complex than the bubble sort.
Method	It is based on the exchanging method.	It uses the selection method.
Speed	In general, the bubble sort runs slower than the heap sort.	In general, the heap sort runs faster than the bubble sort.