Operations on 1D-Arrays
One Dimensional Array Operations
Basic Methods
The fundamental operations enabled by an array are listed below.
- Traverse prints each element of the array one by one.
- Insert a new element at the specified index.
- Delete an element at the specified index.
- Searches for an element based on the specified index or value.
- Update an element at the specified index.
Operation Traverse
Each element of an array is accessed precisely once for processing during an array traversal operation.
This is also known as array visiting.
C code implementation
Let ARR be an unordered Linear Array with N items.
//Program for performing traversing operation.
#include <stdio.h>
void main()
{
int ARR[] = {3, 5, 7, 9, 10};
int i, n = 5;
printf("The elements of the array are:\n");
for(i = 0; i < n; i++)
{
printf("ARR[%d] = %d \n", i, ARR[i]);
}
}
The following output should be generated by this programme:
Output
The elements of the array are:
ARR[0] = 3
ARR[1] = 5
ARR[2] = 7
ARR[3] = 9
ARR[4] = 10
Operation Insertion
One or more data elements are inserted into an array using the insert operation. A new element can be added at the beginning, end, or any provided index of the array, depending on the necessity.
The addition of an element at the end of an array is not always required. A case using array insertion may be as follows:
- Array insertion at the start
- Insertion into an array at a certain index.
- Insertion into an array after the specified index
- Insertion of data into an array before the specified index.
Insertion at the Start of a Sequence
When data is inserted at the start, it causes all existing data items to move one step lower. We create and test an algorithm for inserting an element at the start of an array.
Algorithm
We'll suppose A is an N-element array. MAX specifies the maximum amount of items it can hold. First, we'll see if there's any free space in an array to store any element, and then we'll start the insertion procedure.
begin
IF N = MAX, return
ELSE
N = N + 1
For All Elements in A
Move to next adjacent location
A[FIRST] = New_Element
end
C code implementation
#include <stdio.h>
#define MAX 5
void main() {
int arr[MAX] = {50, 60,70, 80};
int N = 4; // number of elements in arr
int i = 0; // loop variable
int value = 40; // new data element to be stored in arr
// print arr before inserting the new element
printf("Printing arr before inserting the new element -\n");
for(i = 0; i < N; i++) {
printf("arr[%d] = %d \n", i, arr[i]);
}
// now shift rest of the elements downwards
for(i = N; i >= 0; i--) {
arr[i+1] = arr[i];
}
// add new element at first position
arr[0] = value;
// increase N to reflect number of elements
N++;
// print to confirm
printf("Printing arr after inserting the new element -\n");
for(i = 0; i < N; i++) {
printf("arr[%d] = %d\n", i, arr[i]);
}
}
The following output should be generated by this programme:
Output
Printing array before inserting the new element -
array[0] = 50
array[1] = 60
array[2] = 70
array[3] = 80
Printing array after inserting the new element -
array[0] = 40
array[1] = 50
array[2] = 60
array[3] = 70
array[4] = 80
Insertion at an Array's Given Index
We are provided the exact place (index) of an array where a new data element (value) must be added in this situation. We'll first see if the array is full, and if it isn't, we'll shift all data pieces one step below from that point. This frees up space for a new data element.
Algorithm
We'll suppose A is an N-element array. MAX specifies the maximum amount of items it can hold.
begin
IF N = MAX, return
ELSE
N = N + 1
SEEK Location index
For All Elements from A[index] to A[N]
Move to next adjacent location
A[index] = New_Element
end
C code implementation
#include <stdio.h>
#define MAX 5
void main() {
int arr[MAX] = {40,50,60,80};
int N = 4; // number of elements in arr
int i = 0; // loop variable
int index = 3; // index location to insert new value
int value = 70; // new data element to be inserted
// print arr before inserting the element
printf("Printing arr before inserting the element -\n");
for(i = 0; i < N; i++) {
printf("arr[%d] = %d \n", i, arr[i]);
}
// now shift rest of the elements downwards
for(i = N; i >= index; i--) {
arr[i+1] = arr[i];
}
// add new element at first position
arr[index] = value;
// increase N to reflect number of elements
N++;
// print to confirm
printf("Printing arr after inserting the element -\n");
for(i = 0; i < N; i++) {
printf("arr[%d] = %d\n", i, arr[i]);
}
}
The following output should be generated by this programme:
Output
Printing arr before inserting the element -
array[0] = 40
array[1] = 50
array[2] = 60
array[3] = 80
Printing arr after after inserting the element -
array[0] = 40
array[1] = 50
array[2] = 60
array[3] = 70
array[4] = 80
In this case, we are provided an array's position (index), after which we must insert a new data element (value). Only the search procedure differs from the previous example; the rest of the actions remain the same.
Algorithm
We'll suppose A is an N-element array. MAX specifies the maximum amount of items it can hold.
begin
IF N = MAX, return
ELSE
N = N + 1
SEEK Location index
For All Elements from A[index + 1] to A[N]
Move to next adjacent location
A[index + 1] = New_Element
end
C code implementation
#include <stdio.h>
#define MAX 5
void main() {
int arr[MAX] = {40, 50, 60, 80};
int N = 4; // number of elements in arr
int i = 0; // loop variable
int index = 2; // index location after which value will be inserted
int value = 70; // new data element to be inserted
// print arr before inserting new element
printf("Printing arr before inserting new element -\n");
for(i = 0; i < N; i++) {
printf("arr[%d] = %d \n", i, arr[i]);
}
// now shift rest of the elements downwards
for(i = N; i >= index + 1; i--) {
arr[i + 1] = arr[i];
}
// add new element at first position
arr[index + 1] = value;
// increase N to reflect number of elements
N++;
// print to confirm
printf("Printing arr after inserting new element -\n");
for(i = 0; i < N; i++) {
printf("arr[%d] = %d\n", i, arr[i]);
}
}The following output should be generated by this programme:
Output
Printing array before inserting the new element -
array[0] = 50
array[1] = 60
array[2] = 70
array[3] = 80
Printing array after inserting the new element -
array[0] = 40
array[1] = 50
array[2] = 60
array[3] = 70
array[4] = 80
Insertion before an Array's Given Index
In this instance, we are provided the position (index) of an array into which we must insert a new data element (value). The remainder of the activities are the same as in the previous example, but we search until index-1, which is one place ahead of the specified index.
Algorithm
We'll suppose A is an N-element array. MAX specifies the maximum amount of items it can hold.
begin
IF N = MAX, return
ELSE
N = N + 1
SEEK Location index
For All Elements from A[index - 1] to A[N]
Move to next adjacent location
A[index - 1] = New_Element
end
C code implementation
#include <stdio.h>
#define MAX 5
void main() {
int arr[MAX] = {40, 50, 60, 80};
int N = 4; // number of elements in arr
int i = 0; // loop variable
int index = 2; // index location before which value will be inserted
int value = 70; // new data element to be inserted
// print arr before inserting new element
printf("Printing arr before inserting new element -\n");
for(i = 0; i < N; i++) {
printf("arr[%d] = %d \n", i, arr[i]);
}
// now shift rest of the elements downwards
for(i = N; i >= index + 1; i--) {
arr[i + 1] = arr[i];
}
// add new element at first position
arr[index + 1] = value;
// increase N to reflect number of elements
N++;
// print to confirm
printf("Printing arr after inserting new element -\n");
for(i = 0; i < N; i++) {
printf("arr[%d] = %d\n", i, arr[i]);
}
}
The following output should be generated by this programme:
Output
Printing arr before inserting the element -
array[0] = 40
array[1] = 50
array[2] = 60
array[3] = 80
Printing arr after after inserting the element -
array[0] = 40
array[1] = 50
array[2] = 60
array[3] = 70
array[4] = 80
Representation in Graphics
Consider a five-intuition array.
1, 20, 5, 78, and 30 are the numbers.
The execution will be if we need to insert an item 100 at position 2.
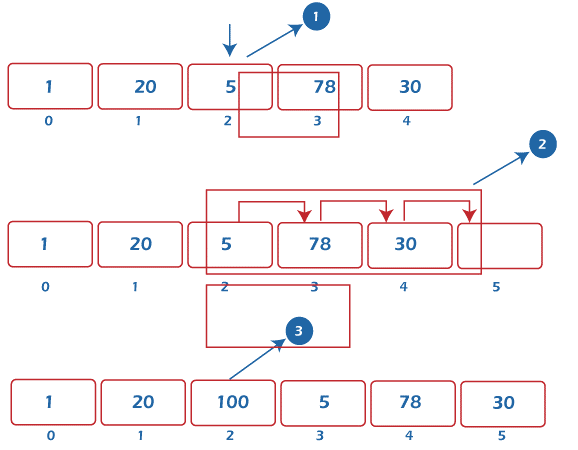
Operation Deletion
Deletion is the process of eliminating an existing element from an array and reorganising all of its elements.
Algorithm
Consider the case when LA is a linear array with N items and K is a positive integer’s position with the value where K<=N. The algorithm to remove an element accessible at the Kth position of LA is as follows.
Start
Set J = K
Repeat steps 4 and 5 while J < N
Set LA[J] = LA[J + 1]
Set J = J+1
Set N = N-1
Stop
C code implementation
#include <stdio.h>
void main() {
int ARR[] = {2,4,6,8,9};
int k = 2, n = 5;
int i, j;
printf("The original array of elements are :\n");
for(i = 0; i<n; i++) {
printf("ARR[%d] = %d \n", i, ARR[i]);
}
j = k;
while( j < n) {
ARR[j-1] = ARR[j];
j = j + 1;
}
n = n -1;
printf("The array elements after deleting the element:\n");
for(i = 0; i<n; i++) {
printf("ARR[%d] = %d \n", i, ARR[i]);
}
}
The following output should be generated by this programme:
Output
The original array of elements are :
ARR[0] = 2
ARR[1] = 4
ARR[2] = 6
ARR[3] = 8
ARR[4] = 9
The array elements after deleting the element:
ARR[0] = 2
ARR[1] = 6
ARR[2] = 8
ARR[3] = 9
Operation of Search
A search for an array element can be done using its value or index.
Algorithm
Consider the case when LA is a linear array with N items and K is a positive integer’s position with the value where K<=N. The algorithm for finding an element with the value ITEM using sequential search is as follows.
Start
Set J = 0
Repeat steps 4 and 5 while J < N
IF LA[J] is equal ITEM THEN GOTO STEP 6
Set J = J +1
PRINT J, ITEM
Stop
C code implementation
#include <stdio.h>
#define MAX_SIZE 100 // Maximum array size
int main()
{
int array[MAX_SIZE];
int size, i, fun_search, found;
/* Input size of array */
printf("Enter size of array: ");
scanf("%d", &size);
/* Input elements of array */
printf("Enter elements in array: ");
for(i=0; i<size; i++)
{
scanf("%d", &array[i]);
}
printf("\nEnter element to search: ");
scanf("%d", &fun_search);
/* Assume that element does not exists in array */
found = 0;
for(i=0; i<size; i++)
{
/*
* If element is found in array then raise found flag
* and terminate from loop.
*/
if(array[i] == fun_search)
{
found = 1;
break;
}
}
/*
* If element is not found in array
*/
if(found == 1)
{
printf("\n%d is found at position %d", fun_search, i + 1);
}
else
{
printf("\n%d is not found in the array", fun_search);
}
return 0;
}
The following output should be generated by this programme:
Output
Enter size of array: 10
Enter elements in array: 11 13 21 26 14 11 10 41 61 6
Enter element to search: 41
25 is found at position 8
Operation Update
The update action updates an existing element in the array at a specified index.
Algorithm
Consider the case when LA is a linear array with N items and K is a positive integer’s position with the value where K<=N. The algorithm to update an element accessible at the Kth location of LA is as follows.
Start
Set LA[K-1] = ITEM
Stop
C code implementation
#include <stdio.h>
void main() {
int ARR[] = {2, 4, 6, 8, 9};
int k = 4, n = 5, item = 100;
int i, j;
printf("The original array elements are as follows :\n");
for(i = 0; i<n; i++) {
printf("ARR[%d] = %d \n", i, ARR[i]);
}
ARR[k-1] = item;
printf("The array elements after updation are as follows :\n");
for(i = 0; i<n; i++) {
printf("ARR[%d] = %d \n", i, ARR[i]);
}
}
The following output should be generated by this programme:
Output
The original array elements are as follows :
ARR[0] = 2
ARR[1] = 4
ARR[2] = 6
ARR[3] = 8
ARR[4] = 9
The array elements after updation are as follows :
ARR[0] = 2
ARR[1] = 4
ARR[2] = 6
ARR[3] = 100
ARR[4] = 9