Compare Balanced Binary Tree and Complete Binary Tree

Complete and balanced binary trees are important and general topics in the concept – Tree data structure. Before discussing the complete and balanced binary tree, we need to have an idea of the tree data structure.

Data structures

Data management is called database management. This allows the computer to sort or organize the data for efficient retrieval.

A data model is a system used to store, manage, and optimize computing resources.

Data processing is not just about data storage. Almost every app or program has notices and updates about its version. Data structures are so simple and complex that it is difficult to program with a programming language that does not have data structures.

Data processing is the process of using intelligence and software to manage, organize, store and store information on a computer device or system. Data models provide visualization for easy data organization and management.

Any basic process, program, or program has two parts: data and algorithms - the rules and regulations of data exchange and algorithms.

There are two types of data structures:

1. Linear Data structures.
2. Non-linear data structures.

Linear Data structures

This data type adds data to the data type. It's all about the process. You can then delete the duplicate. There are four types of linear data, they are:

1. Queue
2. Stack
3. Linked lists
4. Array

Non-linear Data structures

Data formats can be created in a variety of ways. There are two types of interpersonal communication:

1. Tree data structure
2. Graph data structure

Tree data structures

A non–linear data structure that is hierarchical is known as the tree data structure. A node of a tree can have any number of children. Numerous data structures are used in computer science to organize data into different formats. One of them that simulates a hierarchical tree structure and is extensively used is a tree. A tree typically consists of a root value and child nodes that branch out of its parent nodes to form subtrees. Non-linear data structures include trees.

There is no cap on how many child nodes a standard tree data structure can store. The binary tree and its various varieties are a particular tree data structure that will be covered in this article.

 A tree data structure is classified into six types:

1. Available trees.
2. Binary trees.
3. Binary search trees.
4. AVL tress (Adelson, Velsky and Em Landis tree).
5. Red – Black Tree.
6. N – ary Tree.

Binary trees

It is non–linear and hierarchical. A binary tree has a few limitations added to the definition of a tree data structure. A tree data structure in which any node can have a maximum of 2 child nodes (left child node, right child node) is known as a binary tree data structure. In binary trees, we come across the following terms frequently.

1. Parent node – The node that comes just before a given node (child node) when an edge connects both nodes; then, it is known as the parent node of the given node in a binary tree.
2. Child Node – The node that comes just after a given node (parent node) when an edge connects both nodes; then, it is known as a child node in a binary tree.
3. Degree of a node – The number of a child node that a parent node possess is considered to be the degree of that node in a binary tree data structure.
4. Internal node – The nodes with both a parent node and a child node are considered internal nodes in a binary tree data structure.
5. External node – The nodes in a binary tree data structure, excluding all the internal nodes, are considered external nodes in a binary tree data structure.
6. Level – For a selected node in a given binary tree data structure, the number of edges connecting the node and the root node is considered the level of the given node.
7. Height - For a selected node in a given binary tree data structure, the number of edges that connect the node and the root node is considered the height of the given node.

Binary trees are classified into the following types:

1. Rooted binary tree.
2. Full binary tree.
3. Perfect binary tree.
4. Complete binary tree.
5. Almost an entire binary tree.
6. Infinite real binary tree.
7. Degenerate or Pathological Tree.
8. Skewed binary tree.
9. Balanced binary tree.
10. Extended binary tree.

Complete Binary trees

Complete binary trees are unique types of trees that are classified under binary tree data structure. They come with some added limitations to the rules of a binary tree. The levels of these complete binary trees are filled, except for the last level, where the nodes are permeated to as left as possible. Excluding the final level, all the remaining levels in a given binary tree data structure are filled.

We can observe that the above tree satisfies all the rules mentioned in the definition of a complete binary tree. It is a binary tree (i.e., each node in the tree has a maximum of two child nodes) and is filled at each level except for the last level, where the nodes are permeated to as left as possible.

Properties of a Complete Binary tree

1. Complete binary trees are unique types of trees that are classified under binary tree data structures.
2. They come with some added limitations to the rules of a binary tree.
3. The levels of these complete binary trees are filled, except for the last level, where the nodes are permeated to as left as possible.
4. The depth of all the leaf nodes in a complete binary tree is the same, then is known as a proper binary tree.
5. Excluding the final level, all the remaining levels in a given complete binary tree data structure are filled.
6. In a complete binary tree, the level of the leaf node must be equal to the depth of the same node.
7. They are also called almost complete binary trees.
8. The node in the last level of a given complete binary tree can have only a single child node.

Applications of a Complete Binary tree

1. Complete binary trees are useful in writing heap sort algorithms.
2. Any help sort-based data structure applies the complete binary tree.

Balanced binary tree.

Any node's left and right subtree heights cannot differ by more than one in a balanced binary tree, commonly referred to as a height-balanced binary tree.

The prerequisites for a height-balanced binary tree are as follows:

1. There must be at most one difference between the left and right subtrees for any given node.
2. The balance of the left subtree.
3. The balanced right subtree.

Height balanced tree

When the heights of the left and right subtrees differ by no more than m, which is often equal to 1, it is said to be a binary tree. The number of edges along the longest path connecting the root node and the leaf node determines the height of a tree.

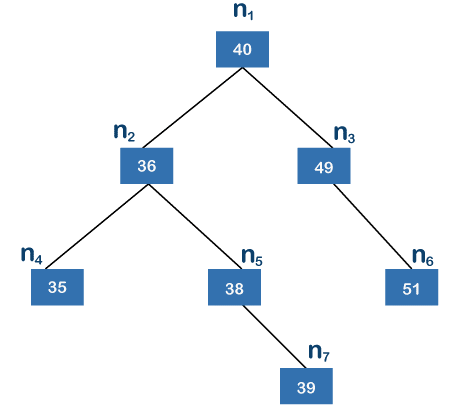
As mentioned earlier, the tree's height is three since node n7 is the furthest away from the root node.

We'll now check to see if the tree is balanced or not. Two leaf nodes numbered, n4 and n7, make up the left subtree. The left subtree is 2 in height. The right subtree's size is one because it has just one edge and one leaf node, n6, respectively. The tree, as mentioned earlier, is height-balanced because we received the value 1. Each node, such as n2, n3, n4, n5, n6, and n7, should go through this procedure of computing the height difference.

As mentioned earlier, the tree's height is three since node n7 is the furthest away from the root node.

We'll now check to see if the tree is balanced or not. Two leaf nodes numbered, n4 and n7, make up the left subtree. The left subtree is 2 in height. The right subtree's height is one because it has just one edge and one leaf node, n6, respectively. The tree, as mentioned earlier, is height-balanced because we received the value 1.

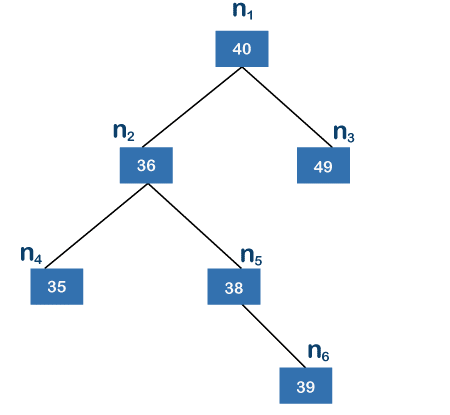
There is no offspring on the left or right of the right subtree. Hence its height is zero.

Need for balanced binary trees

Let's use an illustration to understand further why a balanced binary tree is necessary.

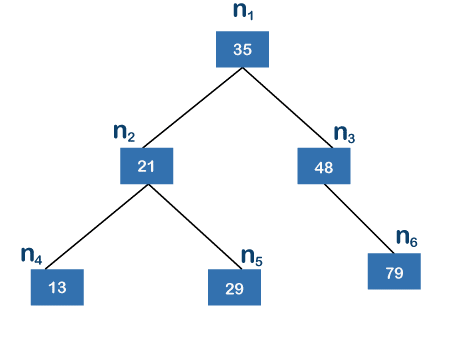
Because every left subtree node is smaller than its parent node and every right subtree node is more prominent than its parent node, the tree, as mentioned earlier, is a binary search tree. Let's say we wish to locate 79 in the tree shown above. Since 79 is more than 35 and not equal to 35, we continue to node n3, or 48. We go to the right child of 48 since the value 79 is more prominent than 48 and not equal to 48. The value 79 of node 48's right child is the same as the value to be searched. The minimum and the maximum number of hops needed to explore any element are 2, while the number of hops required to search element 79 is 2. O is the typical scenario to search an element (logn).

Comparing a balanced binary tree and a complete binary tree

Complete Binary tree

Balanced Binary tree

1. In a complete binary tree, the level of the leaf node must be equal to the depth of the same node. 2. They are also called almost complete binary trees. 3. The node in the last level of a given complete binary tree can have only a single child node. 4. Complete binary trees are unique types of trees that are classified under binary tree data structures. 5. They come with some added limitations to the rules of a binary tree. 6. The levels of these complete binary trees are filled, except for the last level, where the nodes are permeated to as left as possible. 7. The depth of all the leaf nodes in a complete binary tree is the same, then is known as a proper binary tree. 8. The height of a complete binary tree of n number of nodes is given by log (n + 1). 9. Excluding the final level, all the remaining levels in a given complete binary tree data structure are filled.   10. Complete binary trees are useful in writing heap sort algorithms. 11. Any heap sort-based data structure applies the complete binary tree.

1. In a given balanced binary tree, the level of a leaf node might differ from the same node's depth. 2. They are also called proper binary trees. They are also called 2 – Trees. 3. We do not have any rules for the format of filling nodes in a given balanced binary tree. 4. Balanced binary trees are unique types of trees that are classified under binary tree data structure. 5. They come with some added limitations to the rules of a binary tree. In this type of tree, the nodes of the binary tree either have 0 child nodes or two child nodes. 6. They cannot have an odd number of child nodes (since it is a binary tree, in this case, we cannot have any nodes with one child node in the tree.). 7.  We can conclude and determine in simple words by saying that all the nodes in the balanced binary tree have two children; otherwise, they are treated as leaf nodes. 8.  We can conclude and determine in simple words by saying that all the nodes in the balanced binary tree have two children; otherwise, they are treated as leaf nodes. The total number of nodes in a balanced binary is equal to N = [(2(I)) + 1] The total number of internal nodes in a balanced binary is equal to I = [(N – 1) / 2]