Data Structures Tutorial

Data Structures Tutorial Asymptotic Notation Structure and Union Array Data Structure Linked list Data Structure Type of Linked list Advantages and Disadvantages of linked list Queue Data Structure Implementation of Queue Stack Data Structure Implementation of Stack Sorting Insertion sort Quick sort Selection sort Heap sort Merge sort Bucket sort Count sort Radix sort Shell sort Tree Traversal of the binary tree Binary search tree Graph Spanning tree Linear Search Binary Search Hashing Collision Resolution Techniques

Misc Topic:

Priority Queue in Data Structure Deque in Data Structure Difference Between Linear And Non Linear Data Structures Queue Operations In Data Structure About Data Structures Data Structures Algorithms Types of Data Structures Big O Notations Introduction to Arrays Introduction to 1D-Arrays Operations on 1D-Arrays Introduction to 2D-Arrays Operations on 2D-Arrays Strings in Data Structures String Operations Application of 2D array Bubble Sort Insertion Sort Sorting Algorithms What is DFS Algorithm What Is Graph Data Structure What is the difference between Tree and Graph What is the difference between DFS and BFS Bucket Sort Dijkstra’s vs Bellman-Ford Algorithm Linear Queue Data Structure in C Stack Using Array Stack Using Linked List Recursion in Fibonacci Stack vs Array What is Skewed Binary Tree Primitive Data Structure in C Dynamic memory allocation of structure in C Application of Stack in Data Structures Binary Tree in Data Structures Heap Data Structure Recursion - Factorial and Fibonacci What is B tree what is B+ tree Huffman tree in Data Structures Insertion Sort vs Bubble Sort Adding one to the number represented an array of digits Bitwise Operators and their Important Tricks Blowfish algorithm Bubble Sort vs Selection Sort Hashing and its Applications Heap Sort vs Merge Sort Insertion Sort vs Selection Sort Merge Conflicts and ways to handle them Difference between Stack and Queue AVL tree in data structure c++ Bubble sort algorithm using Javascript Buffer overflow attack with examples Find out the area between two concentric circles Lowest common ancestor in a binary search tree Number of visible boxes putting one inside another Program to calculate the area of the circumcircle of an equilateral triangle Red-black Tree in Data Structures Strictly binary tree in Data Structures 2-3 Trees and Basic Operations on them Asynchronous advantage actor-critic (A3C) Algorithm Bubble Sort vs Heap Sort Digital Search Tree in Data Structures Minimum Spanning Tree Permutation Sort or Bogo Sort Quick Sort vs Merge Sort Boruvkas algorithm Bubble Sort vs Quick Sort Common Operations on various Data Structures Detect and Remove Loop in a Linked List How to Start Learning DSA Print kth least significant bit number Why is Binary Heap Preferred over BST for Priority Queue Bin Packing Problem Binary Tree Inorder Traversal Burning binary tree Equal Sum What is a Threaded Binary Tree? What is a full Binary Tree? Bubble Sort vs Merge Sort B+ Tree Program in Q language Deletion Operation from A B Tree Deletion Operation of the binary search tree in C++ language Does Overloading Work with Inheritance Balanced Binary Tree Binary tree deletion Binary tree insertion Cocktail Sort Comb Sort FIFO approach Operations of B Tree in C++ Language Recaman’s Sequence Tim Sort Understanding Data Processing Applications of trees in data structures Binary Tree Implementation Using Arrays Convert a Binary Tree into a Binary Search Tree Create a binary search tree Horizontal and Vertical Scaling Invert binary tree LCA of binary tree Linked List Representation of Binary Tree Optimal binary search tree in DSA Serialize and Deserialize a Binary Tree Tree terminology in Data structures Vertical Order Traversal of Binary Tree What is a Height-Balanced Tree in Data Structure Convert binary tree to a doubly linked list Fundamental of Algorithms Introduction and Implementation of Bloom Filter Optimal binary search tree using dynamic programming Right side view of binary tree Symmetric binary tree Trim a binary search tree What is a Sparse Matrix in Data Structure What is a Tree in Terms of a Graph What is the Use of Segment Trees in Data Structure What Should We Learn First Trees or Graphs in Data Structures All About Minimum Cost Spanning Trees in Data Structure Convert Binary Tree into a Threaded Binary Tree Difference between Structured and Object-Oriented Analysis FLEX (Fast Lexical Analyzer Generator) Object-Oriented Analysis and Design Sum of Nodes in a Binary Tree What are the types of Trees in Data Structure What is a 2-3 Tree in Data Structure What is a Spanning Tree in Data Structure What is an AVL Tree in Data Structure Given a Binary Tree, Check if it's balanced B Tree in Data Structure Convert Sorted List to Binary Search Tree Flattening a Linked List Given a Perfect Binary Tree, Reverse Alternate Levels Left View of Binary Tree What are Forest Trees in Data Structure Compare Balanced Binary Tree and Complete Binary Tree Diameter of a Binary Tree Given a Binary Tree Check the Zig Zag Traversal Given a Binary Tree Print the Shortest Path Given a Binary Tree Return All Root To Leaf Paths Given a Binary Tree Swap Nodes at K Height Given a Binary Tree Find Its Minimum Depth Given a Binary Tree Print the Pre Order Traversal in Recursive Given a Generate all Structurally Unique Binary Search Trees Perfect Binary Tree Threaded Binary Trees Function to Create a Copy of Binary Search Tree Function to Delete a Leaf Node from a Binary Tree Function to Insert a Node in a Binary Search Tree Given Two Binary Trees, Check if it is Symmetric A Full Binary Tree with n Nodes Applications of Different Linked Lists in Data Structure B+ Tree in Data Structure Construction of B tree in Data Structure Difference between B-tree and Binary Tree Finding Rank in a Binary Search Tree Finding the Maximum Element in a Binary Tree Finding the Minimum and Maximum Value of a Binary Tree Finding the Sum of All Paths in a Binary Tree Time Complexity of Selection Sort in Data Structure How to get Better in Data Structures and Algorithms Binary Tree Leaf Nodes Classification of Data Structure Difference between Static and Dynamic Data Structure Find the Union and Intersection of the Binary Search Tree Find the Vertical Next in a Binary Tree Finding a Deadlock in a Binary Search Tree Finding all Node of k Distance in a Binary Tree Finding Diagonal Sum in a Binary Tree Finding Diagonal Traversal of The Binary Tree Finding In-Order Successor Binary Tree Finding the gcd of Each Sibling of the Binary Tree Greedy Algorithm in Data Structure How to Calculate Space Complexity in Data Structure How to find missing numbers in an Array Kth Ancestor Node of Binary Tree Minimum Depth Binary Tree Mirror Binary Tree in Data Structure Red-Black Tree Insertion Binary Tree to Mirror Image in Data Structure Calculating the Height of a Binary Search Tree in Data Structure Characteristics of Binary Tree in Data Structure Create a Complete Binary Tree from its Linked List Field in Tree Data Structure Find a Specified Element in a binary Search Tree Find Descendant in Tree Data Structure Find Siblings in a Binary Tree Given as an Array Find the Height of a Node in a Binary Tree Find the Second-Largest Element in a Binary Tree Find the Successor Predecessor of a Binary Search Tree Forest of a Tree in Data Structure In Order Traversal of Threaded Binary Tree Introduction to Huffman Coding Limitations of a Binary Search Tree Link State Routing Algorithm in Data Structure Map Reduce Algorithm for Binary Search Tree in Data Structure Non-Binary Tree in Data Structure Quadratic Probing Example in Hashing Scope and Lifetime of Variables in Data Structure Separate Chaining in Data Structure What is Dynamic Data Structure Separate Chaining vs Open Addressing Time and Space Complexity of Linear Data Structures Abstract Data Types in Data Structures Binary Tree to Single Linked List Count the Number of Nodes in the Binary Tree Count Total No. of Ancestors in a Binary Search Tree Elements of Dynamic Programming in Data Structures Find cost of tree with prims algorithm in data structures Find Preorder Successor in a Threaded Binary Tree Find Prime Nodes Sum Count in Non-Binary Tree Find the Right Sibling of a Binary Tree with Parent Pointers Find the Width of the Binary Search Tree Forest trees in Data Structures Free Tree in Data Structures Frequently asked questions in Tree Data Structures Infix, Postfix and Prefix Conversion Time Complexity of Fibonacci Series What is Weighted Graph in Data Structure What is the Advantage of Linear Search?

Time and Space Complexity of Linear Data Structures
2023-04-13 18:27:41

Time and Space Complexity of Linear Data Structures

What is Time Complexity?

Time complexity is a concept used in computer science and mathematics to describe the amount of time required for an algorithm to solve a problem as the size of the input data increases. It is a measure of the efficiency of an algorithm, and is usually expressed as a function of the size of the input data. The time complexity of an algorithm is typically measured in terms of the number of basic operations that it performs, such as comparisons, assignments, and arithmetic operations.

The time complexity of an algorithm is important because it helps to determine whether the algorithm is feasible for a given problem size, and to compare the efficiency of different algorithms for the same problem. An algorithm with a lower time complexity is generally considered to be more efficient than one with a higher time complexity, although other factors such as memory usage and implementation details can also affect the overall efficiency of an algorithm.

Time complexity is a measure of the amount of time an algorithm takes to execute as a function of the size of the input data. It is an important concept in computer science because it helps to determine the efficiency of an algorithm, which is a key factor in deciding whether an algorithm is practical for a given problem.

The time complexity of an algorithm is typically expressed using "Big O" notation, which is a way of describing the upper bound of the growth rate of the running time of an algorithm as the input size grows. In other words, it describes how the running time of an algorithm changes as the input size increases.

For example,

  • if an algorithm has a time complexity of O(n), where n is the size of the input data, it means that the running time of the algorithm is proportional to the size of the input data. This is called linear time complexity, because the running time increases linearly with the input size.
  • Other common time complexity classes include O(1), which is constant time complexity, meaning that the running time of the algorithm is constant regardless of the input size.
  • O(log n), which is logarithmic time complexity, meaning that the running time of the algorithm grows at a logarithmic rate as the input size increases.
  • O(n^2) is quadratic time complexity, meaning that the running time of the algorithm grows at a quadratic rate as the input size increases.

The time complexity of an algorithm is typically determined by analyzing the number of basic operations that the algorithm performs, such as arithmetic operations, comparisons, and assignments. By counting the number of these operations as a function of the input size, we can determine the time complexity of the algorithm.

In general, algorithms with lower time complexity are considered more efficient than those with higher time complexity, because they can solve larger problems in less time. However, there are other factors that can affect the efficiency of an algorithm, such as memory usage, so time complexity is not the only factor to consider when evaluating the efficiency of an algorithm.

What is Space Complexity?

Space complexity is a measure of the amount of memory or storage space required by an algorithm to solve a problem, as a function of the size of the input data. It is an important concept in computer science, because algorithms that require a large amount of memory may not be practical for systems with limited resources, such as embedded systems or mobile devices.

Similar to time complexity, space complexity is usually expressed using Big O notation. For example,

  • an algorithm with a space complexity of O(n) means that the amount of memory required by the algorithm grows linearly with the size of the input data.

Space complexity can be determined by analyzing the amount of memory required by an algorithm to store data structures and intermediate results during its execution. For example,

  • if an algorithm needs to store an array of n elements, it will require O(n) space. If the algorithm uses a recursive function that makes n calls, each with its own set of local variables, it will require O(n) space as well.

It is important to note that the space complexity of an algorithm may be different from its time complexity. An algorithm that requires a large amount of memory may have a low time complexity if it can perform its computations in a small number of steps.

Time and Space Complexity of Linear data Structures

1. Array

In computer science, an array is a data structure that stores a collection of elements of the same data type, such as integers, floating-point numbers, or characters, in contiguous memory locations. The elements are accessed by their indices, which are integers that start at 0 and increase sequentially.

Arrays are widely used in programming because they provide an efficient way to store and access a large number of elements. They are particularly useful for tasks that require iterating through the elements in order, such as sorting or searching.

Arrays can be of fixed size or dynamic size, depending on the programming language and the requirements of the program. In some languages, such as C or Java, arrays are a basic data type, while in others, such as Python, arrays are implemented as built-in or external libraries.

It became the model for linked lists, queues, and other data structures.

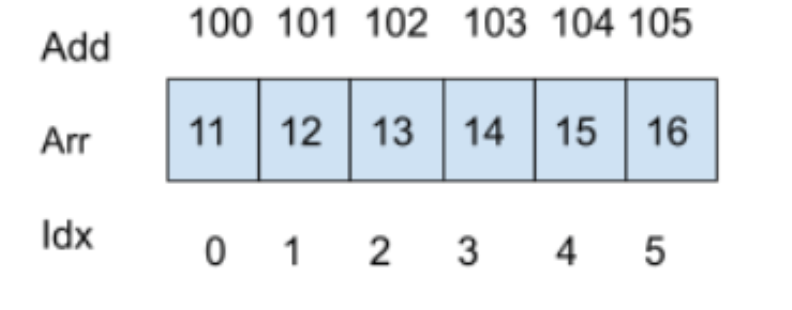
Time and Space Complexity of Linear Data Structures

Time Complexity in arrays of size ‘N’:

  • It takes O(1) time to access an element at a specific memory address because its relative address can be calculated in constant time in an array called "ARR," where the address of the first element is "A" and the size of each element is "S."
  • In a similar vein, editing any array element takes O(1) time.
  • In arrays, the only way to insert a new element at a specific index is to skip all of the elements before that index, which takes O(N) time.
  • O(N) time is required for the deletion operation as well.
  • Without a specific algorithm, the search operation in an array takes O(N) times because we have to iterate over and check each element.

Space Complexity in Arrays:

The space complexity of fetching, overwriting, inserting, and deleting is constant, or O(1), as we do not require additional space to perform any of the aforementioned operations. The auxiliary space consists solely of the space used to construct the array.

2. String

In computer science, a string is a sequence of characters that represent textual data, such as words, sentences, or entire documents. Strings are a fundamental data type in many programming languages, including C, Java, Python, and JavaScript.

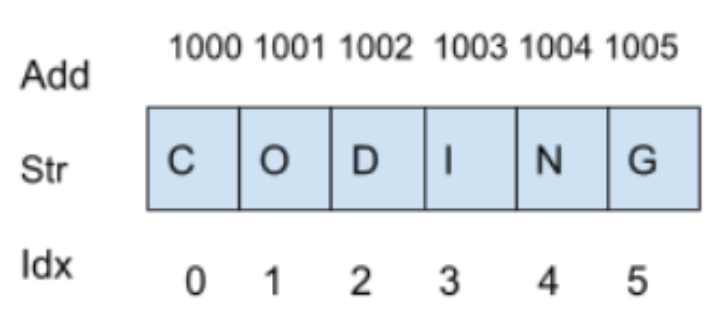
Time and Space Complexity of Linear Data Structures

Time-complexity of Strings with N characters

  • Because, like arrays, its relative index can also be calculated in constant time, reading or editing any character stored at a particular index takes O(1) time.
  • Because we must skip all characters at previous indices, inserting and deleting any character at a particular index in strings takes O(N) time.
  • Because we check for every character in the string, searching for any character in strings takes O(N) time.

Space Complexity in String:

The space complexity of reading, editing, inserting, and deleting is constant, or O(1), as we do not require additional space to perform any of the aforementioned operations. The auxiliary space is only the space used to make the string.

3. Queue

In computer science, a queue is a data structure that allows elements to be added at one end and removed from the other end in a first-in, first-out (FIFO) manner. This means that the first element added to the queue is the first one to be removed. Queues are commonly used in programming to manage resources that are shared by multiple processes or threads.

A queue is conceptually similar to a line of people waiting for service, where the first person in line is the first to be served. The two primary operations supported by a queue are:

  • Enqueue: Adding an element to the back of the queue.
  • Dequeue: Removing an element from the front of the queue.

In addition to these basic operations, queues may also support other functions such as peeking (viewing the first element without removing it), checking if the queue is empty, and determining the size of the queue.

Queues can be implemented using arrays or linked lists. In an array implementation, the front and back of the queue are tracked using indices, while in a linked list implementation, a pointer to the front and back nodes are maintained. Queues are used in a wide variety of applications, including operating systems, network protocols, and simulations.

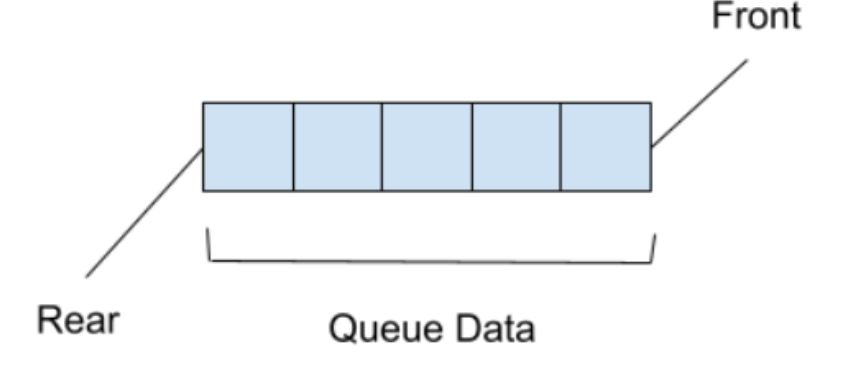
Time and Space Complexity of Linear Data Structures

Time complexity of Queue with N elements:

  • The time required to access or edit any element in a queue is O(N), and in order to reach any given element, all elements after it must be removed.
  • Due to the fact that reaching any particular element necessitates popping the elements stored after it, the searching operation also takes O(N) total time.
  • In a queue, insertion and deletion take the same amount of time, O(1). At any given time, only the front component can be removed, and only the back component can be inserted.

The queue's complexity in space:

Since no additional space is required for any operation, the space complexity of each operation in a queue is O(1).

4. Stack

In computer science, a stack is a data structure that allows elements to be added and removed in a last-in, first-out (LIFO) manner. This means that the last element added to the stack is the first one to be removed. Stacks are commonly used in programming for tasks that require the ability to undo or backtrack, such as in a web browser's back button or in a compiler's parsing of nested statements.

A stack is conceptually similar to a stack of plates, where the top plate is the last one added and the first one to be removed. The two primary operations supported by a stack are:

1. Push: Adding an element to the top of the stack.

2. Pop: Removing an element from the top of the stack.

In addition to these basic operations, stacks may also support other functions such as peeking (viewing the top element without removing it), checking if the stack is empty, and determining the size of the stack.

Stacks can be implemented using arrays or linked lists. In an array implementation, the top of the stack is tracked using an index, while in a linked list implementation, a pointer to the top node is maintained. Stacks are used in a wide variety of applications, including expression evaluation, function call management, and memory allocation.

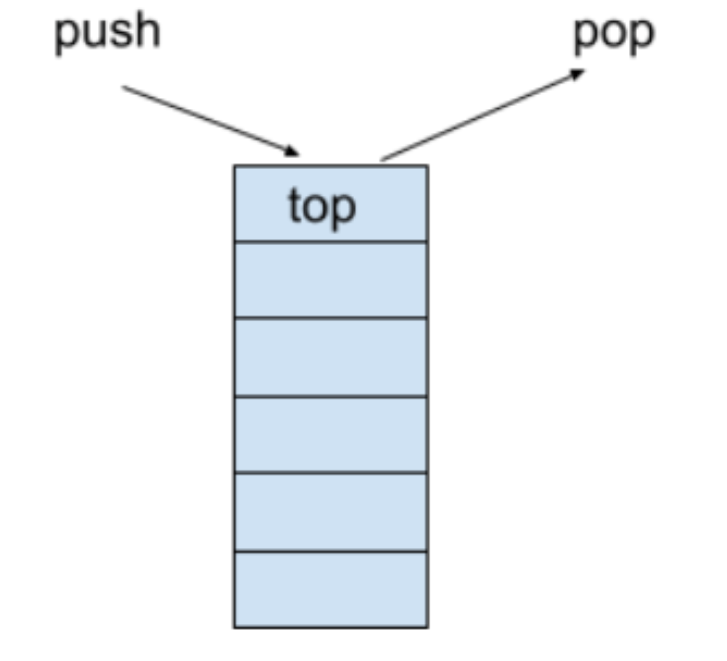
Time and Space Complexity of Linear Data Structures

Time and complexity of a stack with N elements

  • To access or edit any element in a stack, it takes O(N) times the number of elements to reach before it needs to be removed.
  • Due to the fact that reaching any particular element necessitates popping the elements that were stored before it, the searching operation also takes O(N) total time.
  • In a stack, operations like insertion and deletion take O(1) of time.

Space Complexity of Stack

Because no additional space is required for any operation, the space complexity of a stack for each operation is O(1).

5. Linked List

A linked list is a data structure in which data is stored between nodes. A pointer to the next node and a data field make up each node. Pointers are used to link the various elements in a linked list together. In contrast to arrays, elements in a Linked List are not stored in a single memory location but rather in multiple memory locations.

The complexity analysis that follows can be used to comprehend its effectiveness.

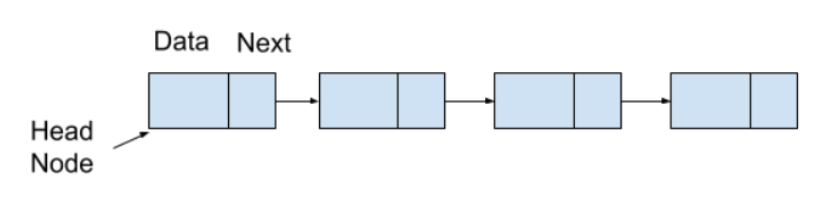
Time and Space Complexity of Linear Data Structures

Time Complexity of a Linked List with N Elements

  • The time complexity of inserting an element into the linked list is O(1) if done on the head and O(N) if done anywhere else because we have to go through the linked list to get there.
  • The time complexity of deletion is O(1) if carried out on the head and O(N) if carried out at any other location due to the necessity of traversing the linked list to get there.
  • The time complexity for searching and accessing any elements is O(N).

Space Complexity of a Linked List

Because no additional space is required for any operation, the space complexity of a linked list is O(1).

Summary

The time and space complexities of linear data structures are summarized in below table:

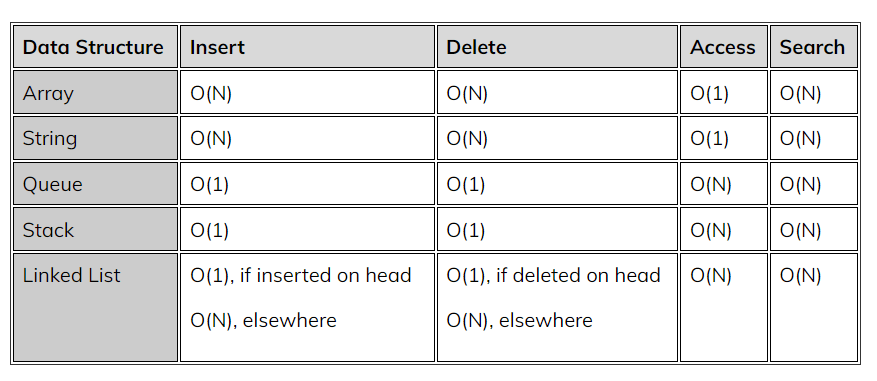
Time and Space Complexity of Linear Data Structures

Where the respective data structure's size is N.