What is an AVL Tree in Data Structure?

AVL tree stands for (Adelson, Velskii, & Landis Tree)

Data structure

Data management is called database management. A data model is a system used to store, manage, and optimize computer resources. Data processing is not just about data storage. Almost every app or program has notices and updates about its version. Data structures are so simple and complex that it is difficult to program with a programming language that does not have data structures.

Data processing is the process of using intelligence and software to manage, organize, store and store information on a computer device or system. Data models provide visualization for easy data organization and management. Any basic process, program, or program has two parts: data and algorithms - the rules and regulations of data exchange and algorithms.

There are two types of data structures

1. Linear Data structures.
2. Non-linear data structures.

Linear Data structures

This data type adds data to the data type. It's all about the process. You can then delete the duplicate. There are four types of linear data, they are:

1. Queue
2. Stack
3. Linked lists
4. Array

Non-linear Data structures

Data formats can be created in a variety of ways. There are two types of interpersonal communication:

1. Tree data structure
2. Graph data structure

Tree Data structure

The information about the tree is self-explanatory.

Tree A node-based data model that represents and supports the structure as a structure. In an asynchronous database, data is stored in a tree data structure called a database. All data types are stored in a central location. Each line of text is called the lower branch of the data type tree.

Two types of plants. This is limited to confidential information. Because this data processing is an individual process. This means that a binary plant can produce 0, 1, or 2 seeds at any time. Binary search trees can quickly parse nested and linked expressions. This allows binary trees to provide values ??from list and associate arrays. It is easy to find hidden items. (because it is a powerful data structure)

Types of trees in data structures

Now that we know what trees are let us now learn the different types of trees in data structures.

There are six types of trees in data structures, and they are mentioned below:

1. General tree
2. Binary tree
3. Binary search tree
4. AVL tree (Adelson, Velskii, & Landis Tree)
5. Red-Black tree
6. N array tree

AVL tree (Adelson, Velskii, and Landis Tree)

The programmers Adelson, Velskii, and Landis, invented the AVL tree (Adelson, Velskii, & Landis Tree) in 1992. AVL tree (Adelson, Velskii, & Landis Tree) is a height-balancing search tree.

Note

Height balanced node

To calculate the height balance of each node, we need to calculate the heights of both the subtrees of that node which leads to a recursive and non-practical approach. All the nodes of a given tree data structure store their respective data and maintain the information regarding the height balance values of its child nodes.

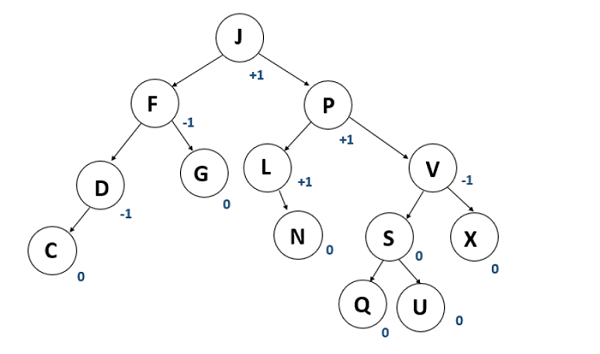
The difference between nodes of left and right sub-trees is known as the balancing factor in a tree data structure. The balancing factor of an AVL tree (Adelson, Velskii, & Landis Tree) is between – 1 and 1 (i.e., - 1 or 0 or 1).

Balancing factor = height of right subtree – height of left subtree

1. We can conclude that the left subtree of a given node in an AVL tree (Adelson, Velskii, & Landis Tree) tree is higher than the right subtree by one level if the balancing factor of the node is 1.
2. Similarly, we can also conclude that the right subtree of a given node in an AVL tree (Adelson, Velskii, & Landis Tree) tree is higher than the left subtree by one level if the balancing factor of the node is 1.
3. And it is clear that both the left subtree and the right subtree of a given node in an AVL tree (Adelson, Velskii, & Landis Tree) are on the same level if the balancing factor of the node is 0.

Here is an example of an AVL tree (Adelson, Velskii, & Landis Tree) tree:

Complexity

Let us look at the complexities of an AVL tree (Adelson, Velskii, & Landis Tree).

The worst-case space complexity of an AVL tree (Adelson, Velskii, & Landis Tree) is O (n), and the average case space complexity of an AVL tree (Adelson, Velskii, & Landis Tree) is O (n).

The worst-case search complexity of an AVL tree (Adelson, Velskii, & Landis Tree) is O (log n), and the average case search complexity of an AVL tree (Adelson, Velskii, & Landis Tree) is O (log n).

The worst-case insertion complexity of an AVL tree (Adelson, Velskii, & Landis Tree) is O (log n), and the average case insertion complexity of an AVL tree (Adelson, Velskii, & Landis Tree) is O (log n).

The worst-case deletion complexity of an AVL tree (Adelson, Velskii, & Landis Tree) is O (log n), and the average case deletion complexity of an AVL tree (Adelson, Velskii, & Landis Tree) is O (log n).

Why should we use the AVL tree (Adelson, Velskii, & Landis Tree)?

An AVL tree (Adelson, Velskii, & Landis Tree) does not let a binary search tree be skewed. By this, it controls the height of it. It takes O (h) time to perform all the operations in a binary search tree.

Operations that can be performed in an AVL tree (Adelson, Velskii, & Landis Tree)

We can perform all the operations that are performed on a binary tree in an AVL tree (Adelson, Velskii, & Landis Tree). Mostly we perform the insertion, searching, traversing, and deletion operations in the AVL tree (Adelson, Velskii, & Landis Tree). The searching and traversing operations are the same as in binary search, but the insertion and deletion operations need to be revisited.